重力梯度传感器结构误差建模

丛丹妮，吴美平，胡小平

（国防科学技术大学机电工程与自动化学院，长沙410073）

0 引言

重力梯度信息不但反映地球表层及内部的密度分布和物质运动状态，还具有很高的军事价值，如提升自主导航精度；提升导弹的命中精度；感应到空间飞行物或水下潜航器，有力破除空中或水下的威胁［1-4］。这些优势使得重力梯度测量成为当今世界重力测量的热点，各国的学者都对它的测量方法进行了各种各样的探索。传统的测量方法性能不佳，超导与原子技术的探索未能得到实际应用［5-7］。 美国Bell Aerospace公司（现并入Lockheed Martin公司）研制的旋转加速度计式的全张量重力梯度仪Air-FTGTM，在军事和商业上都取得了一定的应用，效果良好。我国自20世纪90年代开始研究，截至目前并没有成熟完整的重力梯度仪产品，对重力梯度仪的实物设计、信号提取处理方法上接近空白，基本停留在理论研究、建模仿真阶段。旋转加速度计式重力梯度仪是由多种机械装置组成，加速度计安装精度、旋转机构稳定性、平台稳定性等都会对重力梯度信号准确性产生很大影响［8］。因此，合理限定重力梯度传感器结构精度对于测量结果精度有很重要的意义。而建立与分析结构精度可以从结构误差模型入手，诸多文献均对重力梯度仪的测量原理建立数学模型，但结果各不相同。不同的测量原理模型会推导出不同的结构误差模型，对结构设计和输出结果精度有不同程度的指导意义。本文从牛顿定律入手，进行重力梯度传感器的受力分析，考虑惯性系与非惯性系之间的相对运动，建立了相对完善的测量原理模型、结构误差模型，为进一步的机械精度设计、实物设计、测量和提取信号工作打下基础。

1 单轴旋转调制重力梯度仪测量原理

1.1 重力梯度概念

重力梯度的物理意义是用来描述重力分量因位置而产生的变化，重力梯度为重力位W的2阶导数，即：

重力梯度张量Γ为：

其中，Γxx表示gx在x方向的空间变化率，Γxy表示gx在y方向的空间变化率，Γyy表示gy在y方向的空间变化率等。由偏导数连续求导顺序可交换得：

由场论中的相关知识可知，在地球球体外部重力位处处连续而有限，重力势满足Laplace方程：

综上，只需求解重力位的二次导数中的任意5个相互独立的数值即可得到全部梯度信息。

1.2 重力梯度测量方法与单轴旋转调制概念

早期的扭秤测量利用重力矩的作用可以获得Γxz、Γyz、Γxy、ΓΔ＝Γyy-Γxx4个梯度分量。

旋转加速度计重力梯度仪主要使用加速度计间的比力差值来感应重力的变化率。假设距离为Δl的两个加速度计A1、A2处的重力分别为g1、g2，则A2处的重力可近似用A1处的重力表示为：

加速度计A1、A2的比力输出分别为a1和a2，则a1、a2必然与g1、g2有关。将a1和a2合理组合即可得到Δg＝g2-g1，进一步可以求得加速度计A1处的重力梯度张量。

但是对于重力梯度仪来说，现有加速度计的精度远不能达到要求。地球的重力梯度信号极其微弱，如果测量精度为1E，那么相当于在空间相距10cm的两点重力差值为10-11g［9］。通过大幅度提高材料性能、加工工艺精度或者加速度计的精度性能来达到重力梯度仪的精度需求，目前的相关技术和加工工艺水平还难以达到需求。因此，美国Bell Aerospace Textron公司采用旋转加速度计的理念，通过系统的技术来突破单个元器件的性能极限，从而达到测量微弱重力梯度信号的目标。该公司与澳大利亚联合研制的产品已经成功投入使用［3］，而旋转加速度计式重力梯度仪也是目前唯一获得实际成功应用的、适合机载、船载的梯度测量仪器［10］。

单轴旋转调制重力梯度传感器（Gravity Gradient Instrument，GGI）示意图如图1所示，两对旋转对称且正交的高精度加速度计被安装在转盘上。基于现有加速度计，采用旋转调制技术进一步提高加速度计的使用精度，经过圆盘的匀速旋转，将重力梯度信号调制在两倍转速频率上。这种方法使得GGI可以消除载体运动对加速度计的影响，从而与其他的噪声分离开。

2 重力梯度传感器信号输出模型

就GGI中的加速度计进行比力输出分析，根据Taylor展开：

其中，r为加速度计到圆盘中心的理论距离；a1x是标号为1的加速度计在x方向的加速度；a0x是圆盘中心在x方向的加速度；转盘转动的角速度是ω，则ωt是1号加速度计在重力梯度仪中转过的角。

加速度计只输出敏感轴比力，因此1号加速度计输出比力f1为：

4个加速度计测得信号输出方程为：

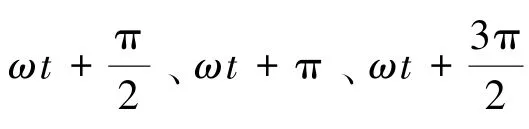
其中，v1、v2、v3、v4具有如下关系：

分别是加速度计敏感轴方向向量。利用加速度计的输出组合，可以解调出梯度分量Γxy、Γxx-Γyy：

旋转加速度计重力梯度仪都是基于矢量差分来工作的， 但文献［8］、 文献［11］～文献［13］都对工作模型进行了推导，却得出了不相同的模型。对于微弱的梯度信号来说，测量模型的完善与否，会大幅度影响测量的精度。由于重力梯度传感器所处的平台稳定系统、系统所在的载体甚至地球严格说来都不是惯性坐标系，本文将着眼惯性系与非惯性系之间的受力分析，对重力梯度传感器圆盘中心加速度以及实际的圆盘中心梯度值进行动力学分析进而建立二者关联模型，进一步推导更为完善的测量模型，为进一步的误差模型分析、机械精度设计、载体平台的稳定性提出要求。

基于动力学分析，加速度计在检测时，由弹簧力与阻尼器阻力均为零时的平衡位置B移动到N，内部结构受力如图2所示。此时，弹簧力阻力平衡加速运动产生的惯性力，并且还受所有天体的万有引力U。

分析加速度计内部质量块的受力，由牛顿第一定律可得：

其中，平衡位置到非平衡位置的位移为sBN；c、k、m分别为阻尼系数、弹簧弹性系数和加速度计质量块质量。考虑在惯性坐标系中，检测质量相对于I的位移为sIN，则绝对加速度a的表达式为：

检测到结果输出时，加速度及系统中，质量块在N点处于平衡，则有：

推导在此状态下敏感轴测量值为：

可忽略除地球外其他天体的引力，考虑圆盘中心真实重力值，建立梯度关系：

其中，sTB是转盘中心到加速度计质量块质心的位移，g0是重力梯度传感器圆盘中心实际梯度值。

推导真实梯度值与加速度计测量值之间的关系，关键点是建立含有各坐标系之间相对惯性坐标系的加速度、相信加速度、Coriolis力的模型。为方便建立各个相关系统之间的受力模型，令地心坐标系为E，载体平台坐标系为P，重力梯度仪传感器转盘坐标系为T，加速度计静态坐标系为S，检测质量坐标系为M。并按各坐标系分解检测质量相对惯性坐标系的位移：

代入式（1）， 并结合式（13）～ 式（15）可抵消sBN并分解其余项：

其中，ωE、ωP、ωT分别是地球自转角速度、载体平台角速度和梯度传感器转盘自转角速度。

综合以上方程，建立a0、g0与加速度计输出之间的关系模型。

重力梯度传感器圆盘上加速度计的输出为：

重力梯度传感器圆盘中心点加速度表达式为：

其中，sTB是重力梯度传感器圆盘坐标系中心点到一个加速度计质心的位移，定义为r：

式（21）是重力梯度载体平台和重力梯度传感器转盘自转角加速度之和。

同样，令式（21）中各向量的分解形式分量为：

带入式（8）中：

理论输出Sout为：

在重力梯度传感器转盘上相对的两个加速度计的输出中，存在对应的差模分量项，输出做和会起到抑制的作用，进一步将相对加速度的和做差会消除载体平台和梯度传感器圆盘转动的影响，消除了一定噪声影响。信号被调制到转盘转速的二倍频，进一步可解调出信号。

3 重力梯度传感器结构误差建模

加速度计安装在转盘上，有6个自由度，安装误差可分为位移误差和角度误差。其中，位移误差分为径向误差、切向误差和高度误差，角度误差分为方向角误差、俯仰角误差和滚转角误差。分别建立相应的误差模型，转速二倍频的信号系数中含有梯度信号与误差项，在假设只存在重力梯度传感器本身的结构误差和转速随机误差的前提下（忽略信号输出过程误差、信号测量误差、信号解调误差等），研究重力梯度传感器结构本身未定系统误差和随机误差的分配。通过合理的误差分配，进而确保结果精度为10E前提下，满足结构精度要求、平台稳定性要求等。

为方便计算，在梯度传感器圆盘上建立与圆盘相对静止的几何坐标系，坐标中心位于圆盘中心，X-O-Y平面位于圆盘上表面，如图3所示。

3.1 径向安装误差模型

径向安装误差为Δrn＝rn-r（n＝1， 2， 3， 4），r为安装半径理论值，rn为实际安装径向长度。以1号加速度为例说明，安装半径理论坐标为（r，0，0），则实际安装径向长度为（r1，0，0）。将实际径向半径rn＝Δrn+r分别代替原来的理论半径：

加速度编号为2、3、4的计算方法与1同理，得到存在径向安装误差时的梯度传感器实际输出SoutΔr为：

其中，aΔr1、aΔr2、aΔr3、aΔr4分别是标号为 1、2、3、4的加速度计在径向误差影响下测量的加速度值。

径向误差模型建立完成，在测量精度要求为10E的前提下，分析误差模型中的输出项。信号从转盘转速的2倍频信号解调，令正弦函数sin2ωt和余弦函数cos2ωt的系数，即输出信号的实际测量幅度值分别为Asin和Acos。在与径向误差之和的耦合过程中，ω的直流分量并不对结果产生影响，而重力梯度传感器圆盘和角加速度之和的分量αPTz在进行Fourier变换后，会在2倍频上叠加一个信号，该信号在2倍频处的幅度值也成为输出信号幅度值中的一项，设为α2ω。

在假设只存在重力梯度传感器本身的结构误差和转速随机误差的前提下（忽略信号输出过程误差、信号测量误差、信号解调误差等），研究重力梯度传感器结构本身未定系统误差和随机误差的分配，这两种误差在合成和分配时可以同等看待，分配方法也完全相同。在等作用原则下分配误差，存在误差函数：

其中，ωc＝（ωEx-ωEy+ωPx-ωPy+ωTx-ωTy）·（ωEx+ωEy+ωPx+ωPy+ωTx+ωTy）是由各系统中转动引起的角速度常数。

等作用原则分配误差，则有：

其中，δα、δR1、δR2、δR3、δR4分别是随机误差α2ω和未定系统误差ΔR1、ΔR2、ΔR3、ΔR4的极限误差。

若忽略转盘转动不稳定的影响，则N＝4，则有：

3.2 切向安装误差模型

1号加速度计理论位置（r，0，0），实际位置（r，yτ， 0）。 其中，yτ ＝rtanΔφ是切向方向安装误差，Δφ是切向方向的线性安装误差导致的初始角安装误差，同时会产生径向长度误差，使径向理论长度rn变为切向误差存在时的实际长度rnΔτ：

与对应Δφn的数量级相比， ｜cosΔφn-1｜的数量级远小于Δφn。因此，初始角径向长度误差可以忽略不计。代入初始角误差，整理得到重力梯度传感器输出误差ΔSΔτ为：

在重力梯度传感器切向误差模型中，不含有随机误差项。第3项为直流分量，对结果不产生影响。在等作用影响前提下，考虑正弦信号的Γxy和余弦信号的Γxx-Γyy，则有：

其 中，δφ1、δφ2、δφ3、δφ4分 别 为φ1、φ2、φ3、φ4的极限误差。则每个加速度计的切向安装极限误差为yτ＝rtanδφ＝rtan2.5E。

3.3 高度安装误差模型

存在高度安装误差时，加速度计位置坐标变为（r， 0，Δh1）。 其中，Δh1是 1号加速度计的高度误差使得圆盘中心点到加速度计的重心的位移在原来基础上增加了z轴方向的位移，向量点积计算后会产生z方向的梯度分量。存在高度误差的输出误差ΔSΔh的表达式为：

其中，Δh1、Δh2、Δh3、Δh4分别是标号为 1、2、 3、 4 的加速度计的高度安装误差，SoutΔh、Sout分别是存在高度误差时的实际输出和理论输出结果。

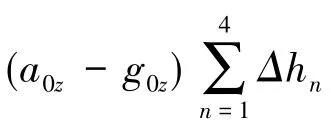
3.4 方向角安装误差模型

切向角安装误差造成了加速度计敏感轴方向的改变，1到4号及速度计改变的角度为ψn（n＝1，2，3，4）。此时敏感轴方向向量变为：

其中，νΔψ1、νΔψ2、νΔψ3、νΔψ4分别是存在方向角误差时，标号为1、2、3、4的加速度计敏感轴实际方向向量将νΔψn代替νn带入原加速度计输出表达式。与理论结果做差，整理得到存在方向角误差时的梯度误差ΔSΔψ为：

其中，SoutΔψ、Sout分别是存在方向角误差时的实际输出和理论输出结果。

而 （a0x-g0x）和（a0y-g0y）各自的 Fourier展开在转速1倍频的项和sinωt、cosωt运算产生2倍频信号，系数设为Cagxω、Cagyω。在对此进行误差补偿的前提下，则有：

等作用原则下，有：

3.5 俯仰角安装误差模型

俯仰角存在安装误差θn，是加速度计绕sTB转动θn，导致了敏感轴方向向量的改变。

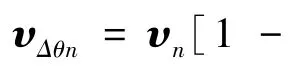
其中，SoutΔθ、Sout分别是存在俯仰角误差时的实际输出和理论输出结果。理想状态下有：

其中，δθn为俯仰角的极限误差。

3.6 滚转角安装误差模型

滚转角的安装误差使得加速度计以敏感轴方向为轴转动，但是该转角既不影响敏感轴方向向量，也不影响圆盘中心到加速度计重心的位移向量，所以并不影响测量以及结果的正常输出。

4 结论

本文从旋转加速度计重力梯度仪测量原理出发，建立了重力梯度传感器的主要结构误差模型。模型反应出各个误差源在输出结果中与信号的耦合项，理论上建立了各个误差对输出结果的影响关系。同时，在精度为10E，重力梯度传感器圆盘直径为400mm的情况下推导出对应精度的具体数值。在理想状态下，只考虑结构误差，按等作用原则分配推导安装极限误差及根据极限误差指导机械设计精度值如表1所示。

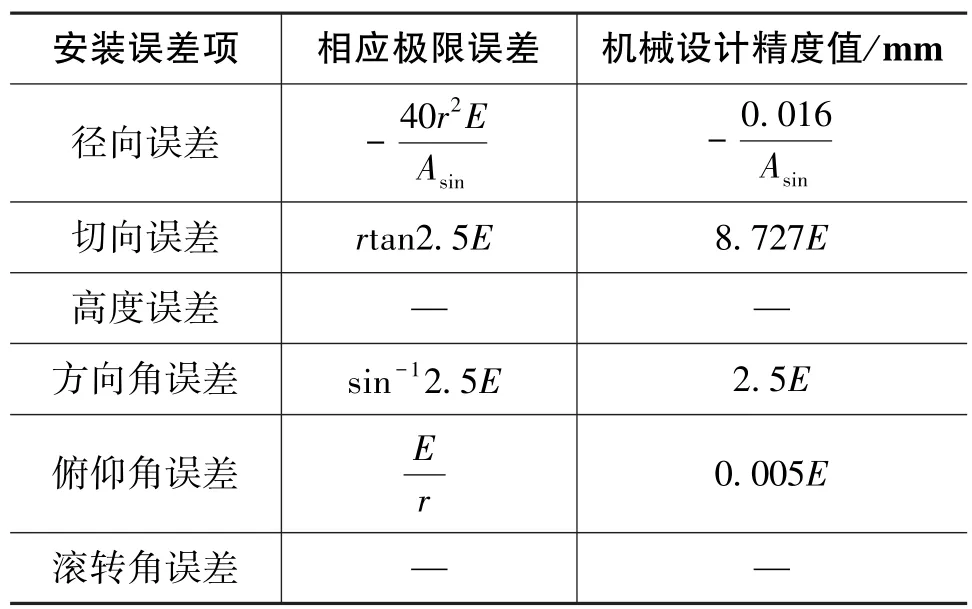
表1 加速度计安装极限误差Table 1 Limiting error in accelerometer installation

极限误差的提出，为进一步提出重力梯度传感器结构精度要求打下基础。给定以10E为测量精度条件下，通过推算的具体精度值发现，除径向误差对机械制造加工工艺有实际的指导意义外，其余精度要求远高于国内现有加工水平，即使超精加工也难以达到要求。为了达到目标测量精度，除突破现有加工工艺水平外，可以通过提高载体平台稳定性，提高相对应加速度计匹配程度等方法减小误差影响，或通过系统误差标定补偿，输出信号处理等方法来保证目标测量精度。

［1］蔡体菁，钱学武，丁昊.旋转加速度计重力梯度仪重力梯度信号仿真［J］. 物探与化探， 2015， 39（S1）： 76-79.CAI Ti-jing， QIAN Xue-wu， DING Hao.Signal simulation of gravity gradient for gravity gradiometer of rotating accelerometer［J］.Geophysical and Geochemical Exploration，2015， 39（S1）： 76-79.

［2］涂良成，刘金全，王志伟，等.旋转重力梯度仪的加速度计动态调节方法与需求分析［J］.中国惯性技术学报， 2011， 19（2）： 131-135.TU Liang-cheng， LIU Jin-quan， WANG Zhi-wei， et al.Methods and requirements of dynamic compensation between accelerometers in rotating gravity gradiometer［J］.Journal of Chinese Inertial Technology， 2011， 19（2）： 131-135.

［3］Harman P G.FALCON BHP billion's airborne gravity gradiometer［C］.Mining 2001 Conference， 2001.

［4］孙中苗，翟振和，李迎春.航空重力仪发展现状和趋势［J］.地球物理学进展， 2013， 28（1）： 1-8.SUN Zhong-miao， ZHAI Zhen-he， LI Ying-chun.Status and development of airborne gravimeter ［J］.Progress in Geophysics， 2013， 28（1）： 1-8.

［5］吴琼，滕云田，张兵，等.世界重力梯度仪的研究现状［J］.物探与化探， 2013， 37（5）： 761-768.WU Qiong， TENG Yun-tian， ZHANG Bing， et al.The research situation of the gradiometer in the world ［J］.Geophysical and Geochemical Exploration， 2013， 37（5）： 761-768.

［6］Macfarlane J， Brett B.Method and system for geophysical data acquisition on an airship ［P］.US Patent： 7236885，2007-06-26.

［7］Van Kann F J， Winterflood J.Gravity gradiometer ［P］.US Patent： 7823449， 2010-11-02.

［8］钱学武，蔡体菁，尹航.一种旋转加速度计重力梯度仪重力梯度解调方法［J］.物探与化探， 2015， 39（S1）： 80-83.QIAN Xue-wu， CAI Ti-jing， YIN Hang.A gravity gradient demodulation method for rotating accelerometer gravity gradiometer［J］.Geophysical and Geochemical Exploration， 2015， 39（S1）： 80-83.

［9］舒晴，周坚鑫，尹航.航空重力梯度仪研究现状及发展趋势［J］.物探与化探， 2007， 31（6）： 485-488.SHU Qing， ZHOU Jian-xin， YIN Hang.Present research situation and development trend of airborne gravity gradiometer ［J］.Geophysical and Geochemical Exploration，2007， 31（6）： 485-488.

［10］涂良成，黄祥青，李祝，等.旋转加速度计重力梯度仪及其关键技术分析［C］.中国地球科学联合学术年会，2014.TU Liang-cheng， HUANG Xiang-qing， LI Zhu， et al.Gravity gradiometer of rotary accelerometer and its key technical analysis ［C］.Annual Conference on Geosciences in China，2014.

［11］刘凤鸣，赵琳，王建敏.基于加速度计重力梯度仪分析与 设 计 ［J］. 地 球 物 理 学 进 展， 2009， 24（6）：2058-2062.LIU Feng-ming， ZHAO Lin， WANG Jian-min.The design and analysis for the accelerometer-based gravity gradiometer［J］.Progress in Geophysics， 2009， 24（6）： 2058-2062.

［12］黄良沛，张圮，罗诗途.平台式航空重力梯度仪测量原理与信号检测［J］.湖南科技大学学报，2009，24（2）： 37-40.HUANG Liang-pei， ZHANG Qi， LUO Shi-tu.Measure principle and signal acquisition of airborne gravity gradiometer based inertial platform ［J］.Journal of Hunan University of Science ＆ Technology， 2009， 24（2）： 37-40.

［13］Talwani M.Non linear inversion of gravity gradients and the GGI gradiometer ［J］.Central European Journal of Geosciences， 2011， 3（4）： 424-434.

［14］Zhu L， Jekeli C.Gravity gradient modeling using gravity and DEM ［J］.Journal of Geodesy， 2009， 83 （6 ）：557-567.