改进Arnold算法和超混沌系统的医学图像加密研究

王倩

摘 要： 针对医学图像的信息安全问题，提出了一种基于改进Arnold置乱和超混沌系统的医学图像加密算法。利用Lorenz超混沌系统生成四组密钥序列；通过最低有效位置换，实现对病人信息的隐藏；利用改进Arnold置乱算法，结合像素位随机取反和异或实现对图像信息的加密。 最后分析了算法的安全性。实验结果表明：算法密钥空间为1067数量级，算法安全性较高，并解决了DICOM（Digital Imaging and Communications in Medicine）图像中病人信息的加密问题，实现了对图像数据和病人信息数据的双重保护，可适用于不同位深，不同源，不等长宽的DICOM格式医学图像的加密，保护病人隐私。

关键词： 医学图像加密； 改进Arnold置乱； Lorenz超混沌系統； 安全性分析； DICOM图像

中图分类号：TP309.7 文献标志码：A 文章编号：1006-8228（2018）02-43-05

Abstract： According to the security problems of patient information and image data in medical images， the paper proposed an encryption algorithm based on the modified Arnold transformation and hyper chaos. The algorithm uses Lorenz maps to build four key sequences according to some rule； uses Least Significant Bit replacing method to hide the patient information； and combined with Pixels' bit-reversed randomized method and XOR method， the modified Arnold transformation is used to encrypt the image data. The security of the algorithm is analyzed. Experimental results show that the algorithm achieves a larger key space in the order of 1067 magnitude， and has a good security. The algorithm can solve the issue of encrypting patient information in DICOM medical digital images. The algorithm， which has the complex rules to generate key sequences， encrypts both image data and patient data. It is suitable for different types of DICOM images， and protects patient privacy.

Key words： medical image encryption； modified Arnold； Lorenz hyper chaos； safety analysis； DICOM

0 引言

医疗系统信息化过程中，为了方便医学影像信息的存储、交换和传输，美国放射学院（American College of Radiology， ACR）和国家电气制造商协会（National Electrical Manufacturers Association， NEMA）共同制定了DICOM标准[1]。随着医院数字化和远程医疗的发展，医学图像越来越易受到窃取和篡改[2-3]。而符合DICOM标准的医学图像除了图像信息外还包含病人姓名，出生日期，检查日期，检查描述等大量隐私信息，因此对医学图像加密研究具有重要意义[4-6]。

对医学图像加密算法的研究，主要运用数字图像加密算法，并结合医学图像的特点予以改进。陈小英[7]等人将AES算法与logistic混沌加密相结合应用于医学图像加密。陈珂[8]等人提出改进的Rijndael算法对医学图像进行加密，具有良好的置乱效果。谭海燕[8]将多混沌组合加密与小波变换相结合提出的医学加密算法同时实现了时域和变换域两方面的加密，但仍只加密了图像信息部分。梁涤青[10]等人利用LeGall5/3整数小波变换，并设计超混沌系统，对医学图像进行加密，大幅度提高了加密效率。A Kanso[11]等人提出一种新颖的混沌加密算法，每轮都包含两个阶段：置乱和扩散，算法适合实时图像加密通信。

然而以上文献并没有考虑病人信息等其他关键信息的加密。对于医学图像这一特殊图像来说，病人信息，检查信息等信息的重要性并不低于图像信息。向涛[6]等人提出改进的AES算法，并将病人信息与图像信息进行互换，实现对病人信息的保护。

医学图像加密除了对图像信息加密外，还需要对病人隐私信息进行加密。本文提出通过最低有效位置换来隐藏病人信息，使得病人信息更分散地分布于图像信息之中，增强了对病人信息的保护，并结合改进的Arnold算法与超混沌系统Lorenz映射实现医学图像信息加密，既可以对病人隐私信息的进行隐藏，又可以有效的实现图像信息加密。

1 Arnold置乱算法与Lorenz超混沌系统

1.1 Arnold置乱算法

Arnold猫映射作为一种二维混沌映射，特别适合图像加密。其变换定义为[12]：endprint

其中（xi，yi）为图像像素点坐标位置，（xi+1，yi+1）为变换一轮后图像像素点坐标位置，图像要求行列值相同大小为N×N。

文献[13]中，G Chen等人对二维Arnold置乱变换进行扩展，引入了参数a和b，变换公式为：

其中，a和b为正整数。

1.2 Lorenz映射

本文算法采用Lorenz映射。其动力学方程为：

其中，σ=10，b=8/3，r>24.74时进入混沌[14]。

2 病人信息隐藏算法

DICOM文件由文件头和数据集两组成，数据集由数据元素组成。数据元素由字段组成：数据元素标签，值长度，值字段和VR[15]。通过查找数据元素标签，就可以从DICOM文件中提取出相应的信息。

本文提出了基于最低有效位置换的病人信息隐藏算法。算法流程如下：

（a） 通过查找标签（0010，0010）定位，找到病人姓名信息数据，并读取值长度信息，将数据保存到PN数组中。

（b） 读取DICOM文件中图像信息，保存为IMGDCM。通过Lorenz映射生成密钥（xp，yp）为基准坐标，按列方向与PN中数据作位置交换，交换算法见步骤c。

（c） 将PN中数据进行位分解，将PN中数据的每一位与IMGDCM由基准坐标确定像素中的最低位进行交换。

（d） 全部数据完成交换后，得到病人姓名信息数组PN'和图像数据IMGDCM'。将PN'和IMGDCM'保存为新的DICOM文件，其他信息不变。

3 改进的Arnold置乱算法

Arnold置乱算法可以简单高效地置乱图像信息，但只能对等长宽的正方形图像进行置乱。本文采取图像分块的方式，并与Lorenz超混沌映射相结合，提出新的置乱算法，可以对非等长宽的图像进行Arnold置乱，并增加了密钥空间。算法使用的Arnold变换公式為式⑵。

算法流程如下：

（a） 读取图像数据IMGDCM，其大小为N×M。以N

（b） 设置Arnold密钥参数（times，a，b），其中times为置乱轮数，a和b为Arnold系数矩阵参数。由Lorenz映射产生密钥Y_1，其长度为times，其值为0或1，由混沌序列产生密钥序列。

（c） 令i=1为此时置乱轮数，对图像分块为大小N×N的子图像IMGDCM1，以图像左下角为基准坐标原点（0，0），则此时子图像右下角坐标为（0，N）。建立一个大小为N×N的窗，并将窗沿x轴滑动，得到一系列大小为N×N的子图像的子图像IMGDCMj，j=1…J，其中J的大小与每次窗口滑动的距离有关，当子图像重叠区域大时，置乱效果更好，但此时子图像数目多，算法效率不高。本文选取滑动距离为。当Y_1（i）=0，由左至右滑动窗口对子图像依次进行Arnold置乱；当Y_1（i）=1，由右至左滑动窗口对子图像依次进行Arnold置乱。

（d） 重复（c），直到i=times。完成times次置乱。

当N>M时，算法与其类似。

以上算法针对的是N≠M的情况，当N=M时。参考文献[16]算法，利用Lorenz映射产生密钥，改变每轮置乱的参数a和b。

4 医学图像加密算法

4.1 加密原理

本算法针对格式为DICOM标准的医学图像，通过Lorenz超混沌映射生成密钥，采用改进的Arnold置乱算法和最低有效位替换对图像数据和病人信息数据进行加密。由于Arnold置乱算法并没有改变像素数据本身的值，对统计攻击抵抗效果不好，因此算法增加了两个步骤改进。一是根据Lorenz超混沌映射生成密钥进行像素随机取反；二是通过Lorenz超混沌映射生成密钥与像素值进行异或。

4.2 密钥生成

文本算法利用Lorenz超混沌映射产生密钥，共四组。分别实现图像像素取反，病人信息隐藏起始位置选取，改进的Arnold置乱以及图像像素异或。设图像大小为N×M，像素位深为w。

密钥生成策略如下。

设置Lorenz映射的初值和系数（x0，y0，z0）和（σ，b，r），迭代生成初始伪随机序列X，Y，Z，并抛弃前面若干值以消除暂态过程，得到准备序列X'，Y'，Z'，序列的长度与图像大小相关。取序列X'的前N×M个值生成第一组密钥序列X_1。取序列Y'的前2个值生成第二组密钥序列Y_1。取序列Y'的3到times+2个值生成密钥序列Y_2，其中times为Arnold加密轮数。Y_2和Y_3共同组成第三组密钥序列，分别为等长宽和非等长宽图像数据加密。取序列Z'的前N×M个值生成第四组密钥序列。

4.3 加密解密算法

加密算法步骤如下：

（a） 读取DICOM文件图像数据和病人信息数据（本文以病人姓名数据为例），分别保存为矩阵IMG和PN，得到图像IMG大小为N×M位深为w，PN长度为。

（b） 像素随机取反加密。将图像矩阵变换为1×（N×M）矩阵IMG1，按照密钥X_1（i）的值进行位取反加密，当X_1（i）=1时，像素值IMG1（i）不变，当X_1（i）=0，像素值IMG1（i）按位取反。将矩阵变换为加密后图像保存为N×M矩阵IMGA。

（c） 最低有效位病人信息隐藏。将图像IMGA和病人信息PN按照2中的算法进行病人信息隐藏。密钥Y_1中的Y_1（1）和Y_1（2）为基准坐标的x和y值。加密后图像和病人信息保存为IMGB和PN'。

（d） 改进的Arnold置乱。对图像IMGB按照3中的算法进行改进的Arnold置乱。若IMGB的行列值不相等N≠M，则使用密钥Y_2进行置乱，若行列值相等N=M，则使用密钥Y_3进行置乱，置乱后图像保存为IMGC。

（e） 图像像素异或。将图像矩阵变换为1×（N×M）矩阵IMGC1，按照密钥Z_1进行异或加密，得到，其中i=1…N×M。将IMGD变换为N×M矩阵IMGD，即为最终图像加密结果。

（f） 保存加密后DICOM文件。将图像数据IMGD和病人信息数据PN'以及其他信息保存到加密后的DICOM文件中，得到最终加密结果。

解密算法为加密算法的逆过程，此处省略。

5 实验结果分析

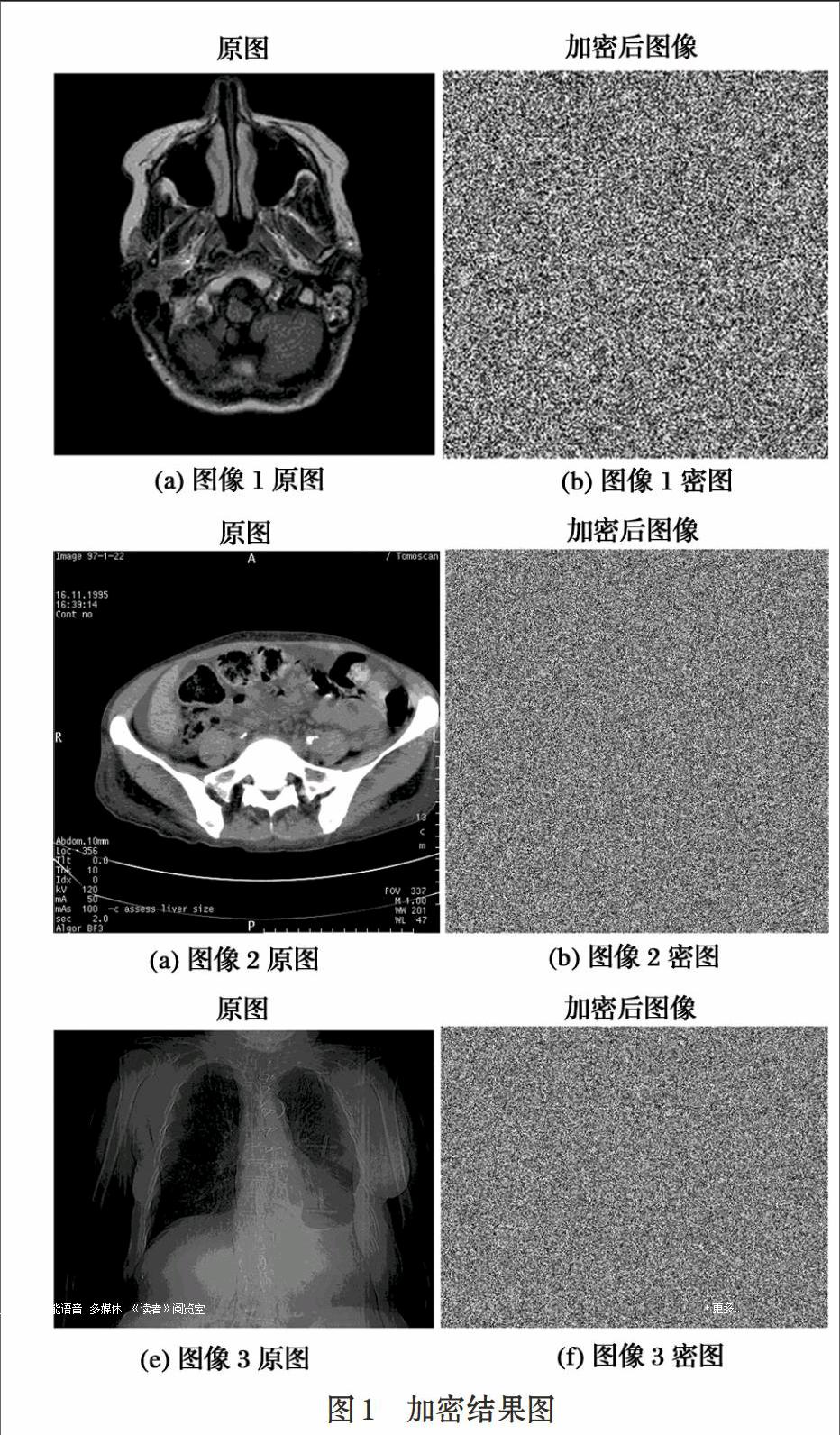
实验选取三组DICOM图像进行算法验证。分别是大小为256*256，位深为16位的MR图像（文中简称图像1），大小为512*512位深为8位的CT图像（文中简称图像2），以及大小为512*400位深为16位的CT图像（文中简称图像3）。由此，可以检验本文算法在对不同图像大小，不同位深，不同源医学图像加密的有效性。实验选取MATLAB R2012作为实验平台。密钥设置Lorenz系数为σ=10，b=8/3，r=30，初值x0=1，y0=1，z0=1，Arnold参数a=2，b=7，加密轮数times=5。实验结果如图1。

实验所用DICOM图像病人姓名为'Anonymized'，以ASCⅡ码表示，图像加密后，图像1中通过标签查看病人姓名为乱码，显示为'>？？1{？v？？T'，其数值为[59198 12748 39547 44150 21682]。通过解密，病人姓名为‘Anonymized，与原始图像相同。同样，对于图像2和图像3也有相似的结果。

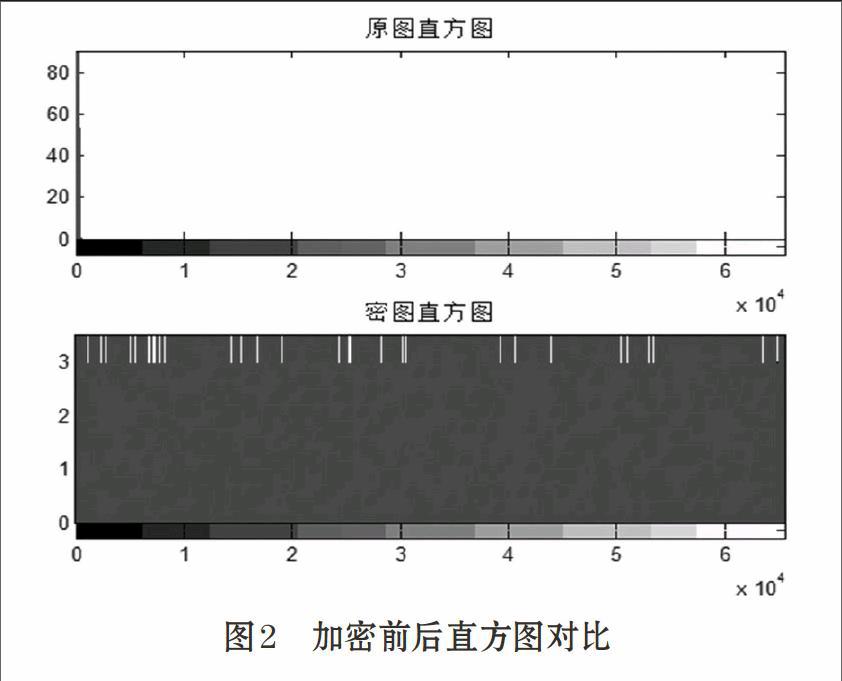
5.1 直方图及信息熵

直方图可直观反映出图像像素灰度值的統计信息，图2为图像1仿真结果，经过本算法加密后，图像直方图比较均匀，可以有效的抵抗通过直方图统计分析获得图像灰度值统计信息的攻击。

图像信息熵可以反映图像的不确定性程度，是图像的另一种统计信息。根据最大离散熵定理，位深为8位的图像最大熵为8，位深为16位的图像最大熵为16。当图像信息熵越接近最大熵，则表示图像的不确定性越大，也就是图像越接近随机图像。表1为实验中图像加密前后的图像信息熵，可以看到16位深图像1和3加密后分别为15.1769和15.7484接近16。8位深图像2加密后为7.9913接近8，近似为随机图像，本算法具有良好的加密效果。

5.2 密钥空间及密钥敏感性分析

本文采用Lorenz混沌映射和改进的Arnold置乱算法加密。密钥为Lorenz中系数r，初值x0，y0，z0，Arnold参数a，b，加密轮数times。密钥空间大小为，具有足够大的密钥空间以抵抗穷举攻击。且在密钥序列生成时，为消除暂态过程需抛掉序列中前x0，y0，z0，个值，并且四组密钥序列可采用不同的策略，这也大大增加了系统的安全性。

对解密密钥改变微小的差别对密图进行解密，以测试密钥敏感性。实验中以x0做微小改变为例进行测试，错误密钥x0=1+1015，其他密钥不变，分别对图3中密图进行解密，以图像1为例结果如图3所示解密后无法恢复原始图像信息，计算图像信息熵如表2，接近随机图像，本算法具有良好的密钥敏感性。

5.3 相关性分析

图像像素相关性可用于分析图像像素之间的关联程度，其计算公式如下

式中，N为图像中选取像素对的总个数，xi 和yi分别为第i对像素的灰度值，和分别为选取两组像素的平均灰度值，γ越接近1则相关性越大，γ越接近0则相关性越小。本文分析图像邻近相关度，随机选取水平方向，垂直方向和对角线方向的邻近像素对各2000个，计算其相关性。结果如表3，加密前图像的邻近相关系数较高，即像素间的关联性较大。加密后图像相关系数降低，像素间的关联性较小。本算法加密效果较好，能够消除像素间的关联性。

使用未进行改进的Arnold置乱算法，文献[4]和文献[10]算法作为对比算法，由于Arnold置乱算法只能对等长宽的图像进行置乱。因此，选择实验图像1进行算法对比。在Arnold置乱轮数相同的条件下，进行图像相关性分析，实验结果如表4。可以看到，本算法去相关性效果比使用Arnold置乱算法要好的多，并且优于文献[10]算法。与文献[4]相比三项参数中有两项去相关性好。

6 结束语

本文提出一种针对DICOM格式医学图像的加密算法。针对医学图像的特点，提出了最低有效位隐藏信息的算法以实现对病人信息的保护。并且对Arnold置乱算法进行改进，改进后算法可以对不等长宽的图像进行置乱，置乱效果好。

参考文献（References）：

[1] Rodrigues J J P C， Compte S S， Diez I D L T. 4-Digital Imaging and Communications in Medicine[J]. e-Health Systems，2016：53-74

[2] Li Xianye， Meng Xiangfeng， Wang Yurong， et al. Secret shared multiple-image encryption based on row scanning compressive ghost imaging and phase retrieval in the Fresnel domain[J]. Optics and Lasers in Engineering，2017.96：7-16

[3] 彭钟贤.基于加密医学图像的信息隐藏算法研究[D].重庆大学硕士学位论文，2014.

[4] 海洁，杜海龙，邓小鸿.基于快速混沌置乱的鲁棒型医学图像加密算法[J].计算机应用，2015.35（2）：430-434

[5] 黄伟琦.基于多混沌系统的医学图像加密算法研究[D].中南大学硕士学位论文，2013.endprint

[6] 向涛，余晨韵，屈晋宇等.基于改进AES加密算法的DICOM医学图像安全性研究[J].电子学报，2012.40（2）：406-411

[7] 陈小英，华英.基于AES的医学图像加密算法[J].中国西部科技，2009.8（24）：19-20

[8] 陈珂，崔志明.改进的加密算法在医学图像上的应用[J].计算机工程与设计，2009.30（3）：752-754

[9] 譚海燕.混沌加密算法在医学图像中的应用研究[D].重庆邮电大学硕士学位论文，2016.

[10] 梁涤青，陈志刚，邓小鸿.基于超混沌映射的医学图像小波域加密算法[J].天津大学学报（自然科学与工程技术版），2016.49（12）：1255-1261

[11] Kanso A， Ghebleh M. An efficient and robust image encryption scheme for medical applications[J]. Communications in Nonlinear Science & Numerical Simulation，2015.24（1-3）：98-116

[12] Niyat A Y， Moattar M H， Torshiz M N. Color image encryption based on hybrid hyper-chaotic system and cellular automata[J]. Optics & Lasers in Engineering，2017.90：225-237

[13] Chen Guanrong， Mao Yaobin， Chui C K. A symmetric image encryption scheme based on 3D chaotic cat maps[J].Chaos Solitons & Fractals，2004.21（3）：749-761

[14] 王英，郑德玲，鞠磊.基于Lorenz混沌系统的数字图像加密算法[J].北京科技大学学报，2004.26（6）：678-682

[15] 王磊.医疗信息系统相关安全技术研究与实现[D].内蒙古科技大学硕士学位论文，2011.

[16] 任洪娥，尚振伟，张健.一种基于Arnold变换的数字图像加密算法[J].光学技术，2009.35（3）：384-387endprint