基于蚁群元胞自动机的地铁行人疏散模型

2018-02-27杜棋东陈柔香许爱军

计算机时代 2018年2期

杜棋东+陈柔香+许爱军

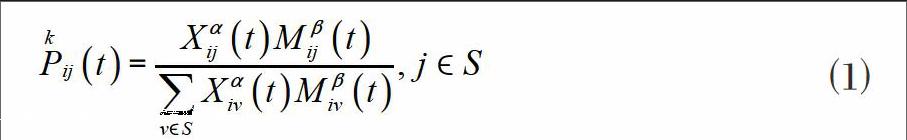
摘要：针对地铁站场结构复杂与疏散受行人主观条件影响等实际情况，宏观上利用蚁群算法解决复杂建筑结构下大客流寻找最优疏散路径，微观上采用元胞自动机智能决策模型，构建融合蚁群算法与元胞自动机的地铁行人疏散模型，并对广州地铁某站场在行人疏散过程中的疏散效率、个体状态等现象进行讨论，其仿真结果可为地铁编制应急预案、员工培训、乘客疏散、应急演练提供参考。

关键词：蚁群；元胞自动机；地铁行人；疏散

中图分类号：TP391.4 文献标志码：A 文章编号：1006-8228（2018）02-18-04

Abstract： Aiming at the actual situation of complex structure and the evacuation of subways affected by the subjective conditions of pedestrians， this paper uses the ant colony algorithm to solve the large passenger flow under complex building structure to find the optimal evacuation path in the macro view， and on the micro level， uses the intelligent decision model of cellular automaton to construct the underground pedestrian evacuation model of the fusion of ant colony algorithm and cellular automaton. And discuss the evacuation efficiency and individual status of a station in Guangzhou Metro during the evacuation of pedestrians. The simulation results can provide the preparation of contingency plans， staff training， the evacuation of passengers， and emergency drills with a reference.

Key words： ant colony； cellular automaton； subway pedestrian； evacuation

0 引言

行人疏散问题一直是交通安全领域的重要研究内容，早在1971年J.Fruin提出行人的平均行进速度与行人密度的关系曲线，这是对行人疏散的第一个重要的研究成果[1]，英国Sime等人和美国Francis分别提出了ORSET 模型 [2]和预测最小理论疏散时间网络模型[3]，这些模型较好地指出了行人在疏散时所选择的逃生路线，但是却忽略了复杂场所以及行人的心理因素对疏散的影响。

作为复杂场所的地铁站场，其行人疏散的研究主要集中在路径算法和疏散模型上，特别是蚁群算法ACO（Ant Colony Optimization）和元胞自动机模型CA（Cellular Automata），王起全等提出蚁群算法能够使地铁行人在较短时间内选择优化的疏散路径[4]，杨敬等模拟楼层拓扑结构，建立楼层蚁群疏散模型，优化运算时间[5]，许爱军等为解决蚁群路径选择的盲目性和随机性，提出基于神经网络自适应蚁群算法[6]，刘真余等对地铁的行人微观建模，基于元胞自动机提出两种疏散规则[7]，田鑫等利用元胞自动机理论创建了地铁车站火灾疏散仿真模型[8]，曹守华等分析地铁通道内行人行走特征，基于蚂蚁元胞自动机对通道双向人流进行仿真，该模型较好地表达了地铁双向通道的行人走行特征[9]，还有学者在智能疏散决策[10-11]，考虑行人引导作用[12]及大型公共建筑疏散[13]等方面有一定的研究。然而上述基于地铁复杂场地结构、大客流以及行人微观特征等综合研究仍不够系统。

本文在文献[4]和文献[11]研究工作的基础上，对地铁站场结构特征和行人的信息处理、决策过程进行系统研究，宏观上利用蚁群算法解决复杂建筑结构下大客流寻找最优疏散路径，微观上采用智能体的元胞自动机智能决策模型，构建融合蚁群算法与元胞自动机的行人疏散模型，并对广州地铁某站场在行人疏散过程中的疏散效率、行人个体状态等现象进行讨论。

1 蚁群与元胞自动机的定义与特征

1.1 蚁群算法

蚂蚁算法真实模拟自然界蚂蚁群体觅食的行为，是一种寻找优化路径的仿生概率型算法，其基本思想是：蚂蚁群体在寻找食物源时，会释放一种信息素，从蚁窝到食物源的路径上，信息素浓度越高的，代表路径越近，蚂蚁会大概率优先选择，并释放信息素增强该路径的浓度，形成正反馈。从上述思想中，得到蚂蚁群体系统模型。

蚁群算法的定义为：定义所有蚂蚁，蚂蚁智能体为k，在t时刻，从位置i转移到位置j的转移概率为：

其中，s为可选择位置点集合，Xij（t）为t时路径（i，j）的信息素强度，Mij（t）为t时刻路径（i，j）的能见度，α、β分别是路径和能见度的相对重要性。蚂蚁群觅食后原路径返回蚁窝，所需时间为u，其对应元素的信息素需要相应调节，重复循环，可找到参数最优路径。

1.2 元胞自动机

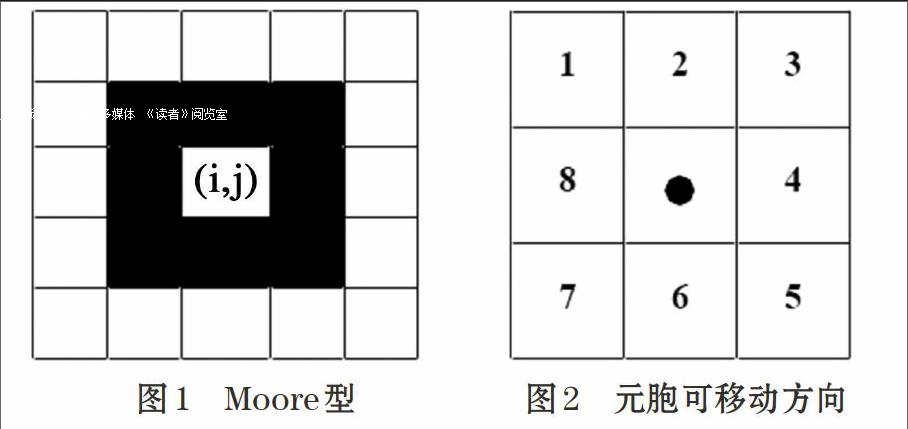
元胞自动机具有时间离散性、空间离散性、同步性、状态离散性和有限性等基本特征，是一种具有时空动态特征的空间动力学研究方法。元胞自动机模型主要由元胞状态集、邻居以及局部规则组成，所有元胞的状态同步更新。更新规则是：第k个元胞在t+1时的状态由自身及邻居的状态共同决定，常见邻居类型有VonNeumann型和Moore型，本文采用Moore型邻，如图1。1，2，3，4，5，6，7，8为元胞移动的可选方向，如圖2。endprint

2 基于蚂蚁元胞自动机的地铁行人疏散模型

2.1 有向图与蚂蚁集合

地铁行人疏散模型基于构建一个有向图G=（V，C，W），其中V为所有路径通道节点，C为节点处元胞集合，W为图中路径ωi集合，其中，ωi路径依次经过路径集合中的各个节点，并且是由蚂蚁在每个路径的元胞集合中选择确定的，长度固定为1（由目标函数确定蚂蚁信息素及转移概率）。蚂蚁集合A1，…，AS，S与路径规模有关，每只蚂蚁从第一个位置，按照转移概率在各条路径上转移直到最后一个位置，转移概率仍然由信息素的强弱确定，而信息素则由目标函数值确定，函数值越小元胞信息素越强，蚂蚁选择的概率越大。一只蚂蚁转移到最后一个位置节点意味着可以停止寻优，每组蚂蚁寻找到n个可行解意味着这组蚂蚁可以停止寻优，一次寻优也称为一次迭代，时间为cycle，在具体的疏散过程中，会明确迭代最大次数或者规定迭代中止条件。

2.2 迭代转移概率

设u=（u0，…，ut-2，ut-1=i）表示某蚂蚁第m次转移前，已路过的各元胞节点组成的地铁通道路径，其中，u0，…，ut-2，ut-1是图的一部分节点，u0是初始节点位置，i是当前节点位置，j是下一节点位置，xij为该元胞节点的信息素，在上述公示⑴的基础上，转移概率为：

在式⑵中，α、β为信息因子和期望因子，Mij（u）为可见度值，Xij（m）为信息素“浓度”，Pij（m，u）表示某蚂蚁在第m次迭代中，构造疏散路径u后，从当前位置i转移到j的转移概率。所有蚂蚁A1，…，AS按照转移概率Pij（m，u）依次转移，构造疏散的可行解；若目前节点位置属于终点元胞集合，则Pij（m，u）=0，意味着蚂蚁在这次迭代中已经完成构造疏散过程。

2.3 信息素浓度

在迭代开始时，设置每个元胞点初始浓度Xij（m）为固定值，之后在每次迭代末，根据⑶进行更新。

在式⑶⑷中，Lij为地铁通道长度，ζij为地铁行人通行难易系数，ρ为蒸发因子，Δτij加上信息素蒸发机制，组成信息素的更新规则。

2.4 模糊推理模型

蚂蚁算法存在的主要问题是容易陷入局部最优解的困局，为了解决这个问题，本文引入模糊推理模型，即在信息素的更新过程中，通过推理再演变，并增加最优路径选择，达到减少陷入局部最优解的概率。考虑对地铁环境较为熟悉的行人在选择路径时主要考虑所处位置到出口的距离以及路径通道上的密度两个因素，路径距离与密度信息均属于模糊参数，本文采用文献[11]的模糊推理模型。

在路径距离方面，将元胞可能选择的8个方向距离出口位置进行极差标准化處理，距离分成3个模糊集，，参数分别代表距离近，距离中，距离远；在密度信息方面，在一定的视野范围内，由人群与障碍物共同决定，密度分成3个模糊集，参数分别代表数量少，数量中，数量多。距离模糊集D和密度模糊集T均作为元胞输入，输出方向移动可能性为，其参数分别代表负大，负中，零，正中，正大，其模糊推理规则如表1所示。

表1所示基本原则为：如果距离某个出口远，障碍物密度大，那么往该出口移动可能性小；如果距离某个出口近，障碍物密度小，那么往该出口移动可能性较大。

3 仿真与验证

3.1 测试环境

为了验证基于蚁群元胞自动机的地铁行人疏散方法的有效性，选取广州地铁某站场进行仿真实验。用于行人出入口的位置有10处，对角线A、B、C、D为地铁出入口，E～J为地铁出入闸机口[6]，如图3所示。

3.2 测试结果

在测试实验中，将地铁平面空进行0.4m*0.4m的网格划分，行人均匀分布在站厅各个位置，在每一时刻上，网格都有可能被障碍物占有，初始化行人数量为30（数量最多不超过300），信息素初始浓度值为0.5，蒸发因子为ρ为0.32，行人当中有60%对地铁站厅环境熟悉，有40%对环境不熟悉。

从图4可以看出，对比其他三种疏散算法，最短路径算法效率最低，行人仅以距离出口近作为惟一出逃路径缺乏合理的规划，元胞自动机算法基于行人微观特征寻找路径，优于最短路径算法，然而没考虑到数量大的群体行为因素，导致其效率仍不高，标准蚁群算法作为寻找最优路径的算法，使大部分行人移向最优出口，造成一定的拥挤，但效率高于元胞自动机模型。本文方法综合蚂蚁算法与元胞自动机模型二者的特点，疏散效率与其他三种对比较优。

本方法能够对不同类型的行人在不同状态下给出分析。第一种状态：对环境的熟悉程度，从图5可以看出，对环境熟悉的行人，会根据距离和障碍物（人群）密度综合考虑挑选前进的方向，整体的疏散速度比较快。第二种状态：行人不同的体力状态，从图6可以看出，体力较好的行人整体疏散速度，明显优于体力差的行人，实验结果与现实情况较为吻合。

4 结束语

本文在求解上基于种群的进化算法，利用元胞自动机的模糊推理方法，提出基于蚁群元胞自动机的地铁行人疏散模型，能够对不同类型的行人在不同状态下给出分析，解决复杂结构环境下地铁站行人疏散的路径问题。下一步将结合地铁突发事件如火灾、群殴、设备断电等进行模拟疏散，综合分析各种因素，提高疏散模型算法的适应性，为地铁编制应急预案、员工培训、乘客疏散、应急演练提供更为完善的参考。

参考文献（References）：

[1] 王理达.地铁车站人群疏散行为仿真研究[D].北京交通大学硕士学位论文，2006：3-5

[2] 王驰.某地铁站火灾情况下人员安全疏散研究[D].北京交通大学硕士学位论文，2007：3-4

[3] 胡忠日.安全疏散研究的国内外动态和发展趋势[J].消防科学与技术，2001.6：7-8

[4] 王起全，杜艳洋，张心远.蚁群算法在地铁车站内应急疏散的应用[J].消防科学与技术，2015.34（1）：55-58

[5] 杨敬，石明全，韩震峰等.一种蚁群算法疏散模型优化的方法[J].消防科学与技术，2015.34（3）：343-346

[6] 许爱军，苏境迎.基于自适应蚁群算法的地铁人员疏散模型[J].微机处理，2016.1：50-53

[7] 刘真余，芮小平，董承玮等.元胞自动机地铁人员疏散模型仿真[J].计算机工程与应用，2009.45（27）：203-248

[8] 田鑫，苏燕辰，李冬等.地铁车站火灾疏散仿真分析[J].科学技术与工程，2017.17（16）：333-338

[9] 曹守华，袁振洲，赵丹等.基于蚂蚁元胞自动机的地铁通道双向行人流仿真[J].系统仿真学报，2009.21（8）：2457-2462

[10] 马洁，徐瑞华，李璇等.地铁车站乘客疏散出口选择行为仿真建模[J].同济大学学报（自然科学版），2016.44（9）：1407-1414

[11] 张丽娟，张艳芳，赵宜宾等.基于元胞自动机的智能疏散模型的仿真研究[J].系统工程理论与实践，2015.35（1）：247-253