全站仪中间法测量套用视线高法公式的推导分析

2018-02-27陈晓晖

西部交通科技 2018年12期

陈晓晖

（广西交通职业技术学院，广西南宁 530023）

0 引言

全站仪中间法在各种论文专著中多有论述，但基本都过于深奥繁杂且没有一个统一的计算公式，一般人难以看懂，不利于此法的推广。本文根据高差（VD）的定义，结合水准视线高法测量原理，提出了套用视线高法公式应用于全站仪中间法测量中的概念，推导出简单实用的中间法高程测量计算公式，并对此公式进行应用验算和误差计算。经检验，测量精度可达到二等水准测量标准，证明了此公式的正确性和实用性。

1 全站仪高程测量方法

全站仪三角高程测量有两种方法，分别是对向观测法和中间法。测量教材里采用的是对向观测法，但该方法其实并不科学：每一个测站都需要对中整平，测站点和待测点之间必须通视，在消除误差方面也有一定的缺陷，最致命的是每个测站都需量取仪器高，但仪器高很难精确量取，尤其在山区，如测站点刚好设在凹处，根本无法量取仪器高，因而显得效率低且精度不高。而中间法测量则简捷得多，只需要仪器整平，且精度最高还可达二等水准测量标准，完全适用于各种大中型工程的测量，故在工程测量中以中间法进行高程测量更为合理。

2 全站仪中间法高程测量计算公式的推导及应用

2.1 高差（VD）的定义与水准测量视线高法的关联

全站仪中间法高程测量与水准高程测量在仪器测量步骤方面完全一致，不同的是观测对象。水准仪观测的是水准尺，水准读数只有正数，而全站仪观测的是反射棱镜，高差值有正有负。全站仪里的高差（VD）指的是被观测的棱镜镜高对全站仪仪高的差值，通俗地说就是棱镜镜高（V）减去仪器的仪高（i），用公式表示为VD＝V－i。由于在一个测站里，无论全站仪观测哪个方向，它的仪器高和水准仪一样，都是维持不变的，而水准仪的仪高就等于水准测量的视线高。同理，我们可以把全站仪的仪高也等同于全站仪的视线高，将水准测量视线高公式套用于全站仪中间法测量中，依据观测对象的不同，对视线高公式作一些必要的改动，最终推导出全站仪中间法高程测量公式。

2.2 中间法高程测量计算公式的推导

先列出水准测量视线高法计算公式：

视线高＝后视点高程＋后视读数

任意点高程＝视线高－任意点读数

从图1我们可以看出，全站仪视线高＝后视点高程＋棱镜高－高差。两相对照，可以得出：（1）水准测量后视读数＝后视点棱镜高－后视点高差；（2）任意点读数＝任意点棱镜高－任意点高差。为了更直观地对接视线高法，可以在“棱镜高－高差”两边加上括号。

所以，全站仪中间法高程测量公式可推导成：

视线高＝后视点高程＋（后视点棱镜高－后视点高差）

任意点高程＝视线高－（任意点棱镜高－任意点高差）

图1 中间法仪器架设示意图

我们把视线高取作J，后视点亦是已知点可以取作BM，把棱镜高取作V，把高差取作VD，任意点取作n，则全站仪中间法高程测量计算公式可列式为：

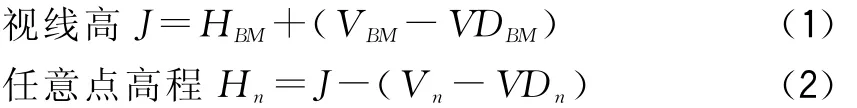
如果在这个测站里，棱镜高没有变化，则公式可简化为：

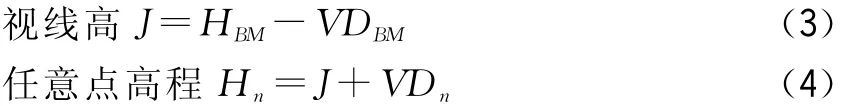
2.3 计算公式的应用

全站仪中间法高程测量的计算表格可参照水准视线高法的表格，下面举例计算。为了更具说服力，所列举数据除了一般数据外，还专门列出一些特殊的数据，比如棱镜高0.5和棱镜高－2。

例：道路中线测量，已知水准点BM1＝95.00m，水准点BM2＝95.21m，求各中桩高程（如下页表1所示）。

视线高J1＝95.00＋（1.3－0.8）＝95.50 H020＝95.50－（1.3＋0.5）＝93.70

H040＝95.50－（0.5－1.0）＝96.00

H060＝95.50－（－2.0－3.0）＝100.50

ZD前＝95.50－（1.6－1.5）＝95.40

视线高J2＝95.40＋（1.3－2.0）＝94.70

H080＝94.70－（2.8＋2.6）＝89.30

H100＝94.70－（1.3＋3.5）＝89.90

复核：fh＝95.20－95.21＝－0.01（m）＝－10（mm）＜fh容＝±50＝±45（mm）

表1 全站仪中间法高程测量计算例表（m）

2.4 全站仪中间法高程测量精度分析

由中间法仪器架设示意图（图1）可看出，采用中间法对待测点进行测量，其精度主要受斜距S1和S2、竖直角1和2、待测点棱镜高V1和V2、大气折光系数K1和K2的影响，无关仪器高。

2.4.1 全站仪中间法高差中误差计算相关参数分析

2.4.1.1 测距中误差 ms

在一个测站只使用一台仪器，认为在对已知点和待测点观测过程中此式可成立：ms1＝ms2＝ms

2.4.1.2 测角中误差 m

测角中误差来源于仪器误差和观测误差。

（1）仪器误差属于系统误差，主要为仪器精度划定，比如使用测角精度为5″级的全站仪，则仪器误差为5″，而使用测角精度为0.5″级的全站仪，仪器误差为±0.5″。

（2）观测误差包括目标偏心误差、读数误差、照准误差，观测误差值等于这三个误差值的平方再开根号。

目标偏心误差指对中杆偏移而导致的竖直角测角误差。测角精度越高的仪器误差值越小，对于0.5″级全站仪可取目标偏心误差值为0。

因全站仪读数是屏幕直接显示，故读数误差为仪器本身的系统误差，对于0.5″级的全站仪，可取读数误差为±0.5″。

照准误差与观测者眼睛瞄准判断的能力以及全站仪望远镜的放大倍数有关，一般会取±2″。

则观测误差m观＝＝2.06″。

而测角中误差m等于仪器误差0.5″平方＋观测误差2.06平方再开根号，推出m＝＝2.1″。

2.4.1.3 大气折光系数中误差 mK

大气折光系数的大小主要取值于空气的密度，而空气密度是变化的，不同时段的系数值存在误差，从研究得知，折光系数误差一般为±0.03～±0.05，因而可以取中间值mK＝0.04。

根据以上的分析论述，可得出在已知点A和待测点B这两点间的高差中误差mhAB＝2sin2×＋2 D2×／ρ2＋1／2 R2×D4×m2K。

由公式可知，mhAB的数值大小是随竖直角α及水平距离D的大小而变化的。为了进一步检测所推导的中间法公式的测量精度，现采用徕卡TS60全站仪进行中间法高程测量，仪器测角精度为±0.5″、测距精度为±0.6mm＋1ppm，最后算出不同竖直角α和水平距离D所对应的每测站高差均值中误差，数据见表2，再换算成以每km为单位的高差中误差，见表3。

表2 徕卡TS60全站仪中间法测量高差均值中误差计算值表

注：＝mhAB

水平距离D（m）20°10 0.09 0.10 0.11 0.13 0.16竖直角α 1° 4° 7° 10° 15°2.06 0.22 20 0.18 0.20 0.21 0.23 0.25 0.28 30 0.30 0.31 0.32 0.34 0.35 0.36 40 0.40 0.40 0.41 0.41 0.42 0.44 50 0.50 0.50 0.51 0.51 0.52 0.53 60 0.61 0.61 0.61 0.62 0.63 0.63 70 0.70 0.70 0.71 0.71 0.72 0.73 80 0.80 0.80 0.81 0.82 0.82 0.83 90 0.91 0.92 0.92 0.92 0.93 0.94 100 1.01 1.01 1.02 1.02 1.02 1.03 200 2.03 2.03 2.04 2.04 2.05

把上表换算成以每km为单位后的高差中误差mhABKM计算值如表3所示：

表3 徕卡TS60全站仪中间法测量每km高差中误差计算值表

注：＝mhAB，n为每km测站数

水平距离D（m）20°10 0.74 0.76 0.81 0.90 1.28竖直角α 1° 4° 7° 10° 15°3.56 1.60 20 1.01 1.06 1.09 1.13 1.21 1.41 30 1.23 1.26 1.29 1.33 1.41 1.52 40 1.46 1.46 1.48 1.51 1.55 1.62 50 1.60 1.62 1.63 1.65 1.67 1.73 60 1.72 1.79 1.83 1.86 1.88 1.92 70 2.01 2.01 2.03 2.05 2.06 2.08 80 2.15 2.15 2.16 2.17 2.17 2.20 90 2.23 2.25 2.25 2.25 2.25 2.28 100 2.26 2.26 2.28 2.28 2.28 2.31 200 3.51 3.51 3.53 3.54 3.54

按《国家一、二等水准测量规范》《国家三、四等水准测量规范》的规定：

二等水准测量每km：偶然中误差MΔ≤1.0mm，全中误差Mw≤2.0mm；

三等水准测量每km：偶然中误差MΔ≤3.0mm，全中误差Mw≤6.0mm。

通过对比表3计算出的中误差值mhABKM可得出以下结论：

（1）当观测角≤7°且两待测点间水平距离≤20m时，采用0.5″级全站仪进行中间法测量，其精度可达到二等水准测量的精度标准。

（2）当观测角≤20°且两待测点间水平距离≤200m时，采用0.5″级全站仪进行中间法测量，其精度可达到三等水准测量的精度标准。

总结以上结论，可以得出：采用本文推导出的中间法高程测量公式进行高程测量，其精度可达到二等水准测量标准，完全符合各类大中型建设工程的高程测量精度要求。