节段预制装配式综合管廊抗震性能研究
2018-02-27王建军李彩霞
刘 营,王建军,李彩霞,刘 卓
(广西路桥工程集团有限公司,广西 南宁 530001)
0 引言
地下综合管廊可以聚集城市基础设施功能,消除地面上“城市蛛网、马路拉链”的不良现状,大幅度提升城市面貌,创造和谐的城市生活环境,有利于保障城市安全,完善城市功能,美化城市景观,促进城市集约高效和转型发展,提高城市综合承载力,增加公共产品有效投资,拉动社会资本投入,打造经济发展新动力[1]。目前国内城市地下综合管廊最为常见的施工方法有明挖现浇法、明挖预制法以及顶管法三种,而预制施工方法又分为节段预制、半预制以及节块预制。预制装配技术是新兴技术,也是目前国家大力推广的技术革新,由此将改变传统工地现场大面积占用土地而造成环境污染的现状,用更快速、更先进、更高效的理念推动城市建设发展,这也意味着我国的城市建设开始从传统走向现代。因此可以肯定,预制装配式施工将会逐渐成为未来城市地下综合管廊建设发展的重要方向。
1995年,阪神地震震害调查发现,埋地管线几乎全部破坏,而敷设在共同沟内的管线基本完好,损失相对较小,只 有共同沟 沟体有轻 微的裂缝[2][3];1933年Long-Beach地震,多处管道损坏;1971年San Femando地震,大量燃气、供水管道受损;1976年唐山大地震,唐山市供水燃气及供水管道系统破坏殆尽,天津市供水系统受损严重;1989年Loma Prieta地震、1994年Northridge地震、1995年阪神地震、1999年台湾地震、“5·12”汶川地震、“3·11”东日本大地震、“4·20”芦山地震等均造成大量供水及燃气管道破坏,进而导致城市大面积停气、停水。多次震害表明,地震是威胁共同沟安全的最大因素[4]。我国位于环太平洋地震带和欧亚地震带,是一个地震多发国家,目前国内已建成及在建综合管廊项目众多,而针对节段预制地下综合管廊的抗震研究还不是很多,因此研究节段预制地下综合管廊的抗震性能,将为预制装配地下综合管廊推广提供一定的理论参考。
1 工程概况
某干线综合管廊工程总长度1.6km,两舱断面设计,断面净尺寸B×H=综合舱3.9m×3m+电力舱2.6m×3m,如图1所示。结构安全等级为一级,结构重要性系数为1.1;防水等级为二级,混凝土抗渗等级为P8。节点部分采用现浇施工,标准段采用节段预制拼装施工。管廊标准节段长1.5m,节段之间采用预应力方式连接,设置三元乙丙弹性橡胶垫、遇水膨胀橡胶和双组分聚硫密封膏进行构造防水,如图2所示。其中单根预应力钢绞线张拉控制力为150kN,每三节管廊张拉一次。地震动反应谱特征周期为0.35s,地震动峰值加速度为0.1g,设计地震分组为第一组,二类场地。为便于下文进行论述,规定沿着预制管廊长度方向为纵向(X轴),管廊横截面水平向为横向(Y轴),重力所在方向为竖向(Z轴),坐标符合右手法则。
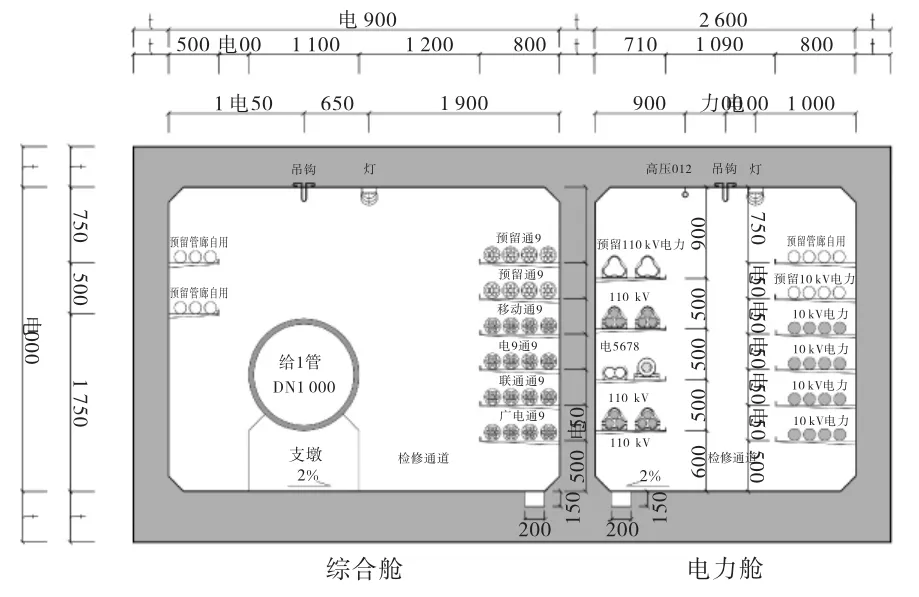
图1 节段预制综合管廊断面图(mm)

图2 节段预制综合管廊接头构造图
2 分析模型
2.1 有限元模型
每一个管廊节段模拟为弹性梁单元,节段之间采用Link单元连接,忽略节段间相对平移,接头转动刚度计算见下节2.2。将节段管廊周围土体假定为集中土弹簧,土弹簧参数取值见下节2.3。在预制拼装与节点现浇位置处,通常设置沉降缝以保证现浇段和预制段的不均匀变形;同时为保证结构连续性,在预制节段端头处预留空心钢管,绑扎现浇段钢筋时插入涂有黄油的钢管中,最后浇筑混凝土。取模型端头处土弹簧刚度为标准节段土弹簧刚度的2倍,以此考虑现浇部分对预制拼装部分的边界影响。选取84m(56个节段)的预制拼装段建立SAP2000有限元分析模型,模型中共168个节点,112个框架单元,55个Link单元。结构计算简图如图3所示。

图3 节段预制管廊梁单元分析模型图
2.2 节段预制管廊接头刚度模型
对于预制拼装结构,节段之间的连接将直接影响着整个结构的使用性能。预制综合管廊的连接方式主要有承插式接头、螺栓连接和预应力筋连接[5]。陈智强[6]考虑接头拼缝变形形态、预应力筋伸长和遇水膨胀橡胶条弹性模量的影响,提出了接头处抗弯刚度计算模型和抗弯承载力计算模型;胡翔[7]通过接头和整体结构足尺模型,对预制综合管廊的受力性能进行研究;张厚美[8]将接头衬垫和连接螺栓抽象成弹簧,建立了接头受力和变形的非线性方程式,推导了接头刚度的简化计算公式。本文在相关学者研究的基础上,基于以下假定:(1)接缝端面满足平截面假设;(2)计算中弹性橡胶垫均未出现拉应变。推导出基于梁单元假设的接头刚度计算模型(见图4),其中遇水膨胀橡胶垫受力较小,忽略不计。

图4 节段预制管廊接头力学分析模型图
在计算时,假设转动角度较小,则θ≈tanθ,首先根据预应力张拉值,由式1推导出弹性橡胶垫初始变形δP0,然后由平截面假定推导出微小转动角度下预应力钢绞线和弹性橡胶垫的几何变形(式2、式3),进而由几何方程、物理方程求得预应力钢筋拉力和弹性橡胶垫压力(式4),最后由截面力学平衡方程(式5)可以求得节段预制综合管廊转动弯矩和转动角度的函数关系。
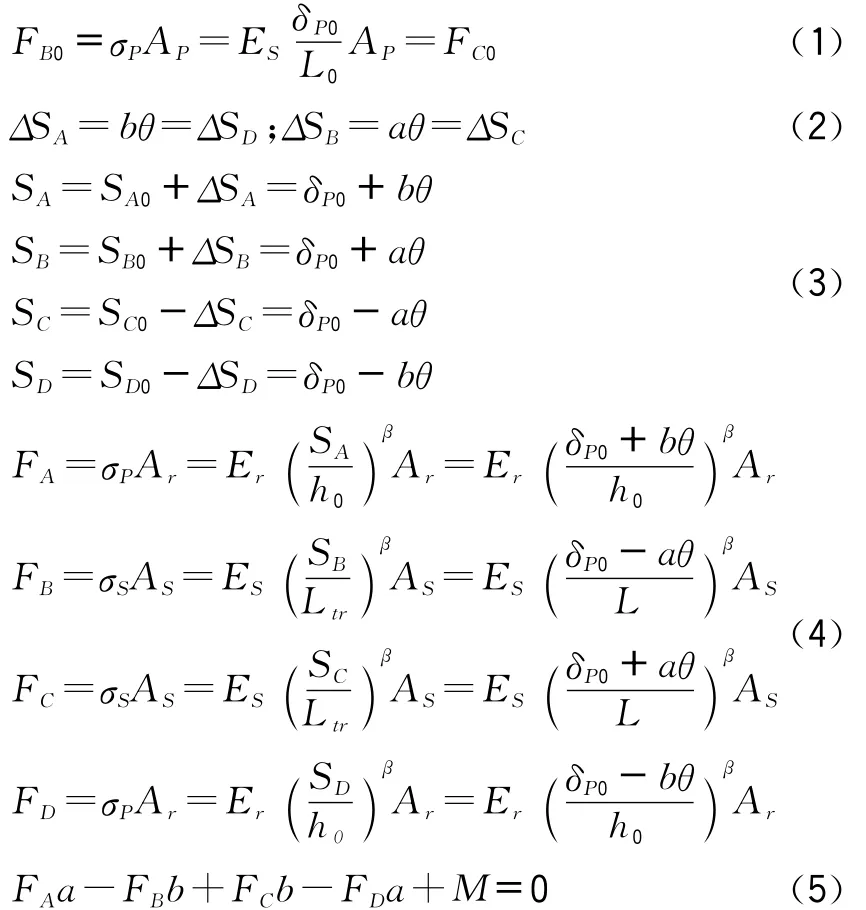
其中:AS——预应力钢绞线面积;
FB0——初始预应力张拉值;
ES——预应力钢绞线弹性模量;
δP0——预应力钢绞线初始变形量;
L0——预应力钢绞线张拉长度;
Er——三元乙丙弹性橡胶垫弹性模量;
Ar——三元乙丙弹性橡胶垫截面面积;
h0——三元乙丙弹性橡胶垫厚度;
α ——预应力钢绞线外形系数;
ftk——混凝土抗拉强度标准值;
d——钢绞线直径;
σ=Erεβ。
由以上接头刚度计算公式求得工程实例中接头横向转动刚度为8.29×108N/m,竖向转动刚度为1.12×109N/m。
2.3 土-结构作用模型
我国城市轨道交通结构抗震设计规范中第6.6中规定:隧道与地下车站结构采用横向地震反应位移法进行计算时(见图5),可将周围土体作为支撑结构的地基弹簧,结构可采用梁单元进行建模[9]。结构横向计算时,地基弹簧刚度可按照下式计算:

式中:k——压缩或剪切地基弹簧刚度(N/m);
K——基床系数(N/m3);
L——垂直于结构横向额计算长度(m);
d——土层沿结构纵向计算长度(m)。

图5 矩形结构反应位移法横向计算示意图
结构采用纵向地震反应位移法进行计算时,地基弹簧刚度可按照下式计算:

式中:kt——沿结构纵向侧壁剪切地基的弹簧刚度;
kl——沿结构纵向侧壁抗压地基的弹簧刚度;
k——压缩或剪切地基的弹簧刚度(N/m)。其余参数同横向地基弹簧刚度计算公式。

图6 矩形结构反应位移法纵向计算示意图
根据地勘资料,场地内岩土层主要为第四系残积相的红黏土,地基基床系数取值参考地基与基础(顾晓鲁)[10]。采用地基弹簧计算方法,其中管廊纵向计算长度为1.5m,横向平均宽度为7.7m,高度为3.8m。得到土弹簧刚度取值:横向地基土刚度为2.28×105N/m;纵向剪切刚度为7.60×104N/m;竖向刚度为4.62×105N/m。
2.4 地震动输入
本文选取7条地震波(峰值调整为0.05g),地震波信息如表1所示,对应反应谱曲线如图7所示,其中前2条地震波为人工波,其余5条为在PEER(Pacific Earthquake Engineering Research Center)地震波数据库上选取实际波。这7条波的峰值加速度PGA与峰值速度PGV的比值范围为5.75~16.92 1/s,覆盖范围较大。其中,地震波沿横向进行输入。

图7 地震波反应谱与规范设计反应谱曲线图

表1 人工波和实际地震波数值表
3 数值响应分析结果
本文主要选取了管廊结构变形、弯矩值、剪力值、地基反力以及管廊接头受力、变形为分析对象,探讨节段预制综合管廊在自重及地震作用下结构受力特征,下文按照7条地震波的平均值结果进行分析。
3.1 自重作用

图8 节段预制管廊自重作用下接头弯矩曲线图
由图8可知,节段预制管廊在自重作用下接头弯矩呈现对称分布,在1/7和6/7跨径范围内弯矩达到最大值,最大值为1.8×106N/m,在1/2跨径处弯矩出现最小值,最小值为-1.5×105N/m,其余部分呈现曲线连续变化,节段预制管廊结构如同两跨连续梁弯矩变化趋势。这主要是受管廊结构两端面(与现浇结合位置处)地基弹簧刚度较大的(端头处地基土弹簧刚度为中间标准土弹簧刚度的2倍)影响,使得跨径中间位置出现负弯矩,而管廊结构为箱型薄壁结构,因此跨径中间处管廊顶板位置的弹性橡胶垫首先会出现压缩量减弱的趋势。
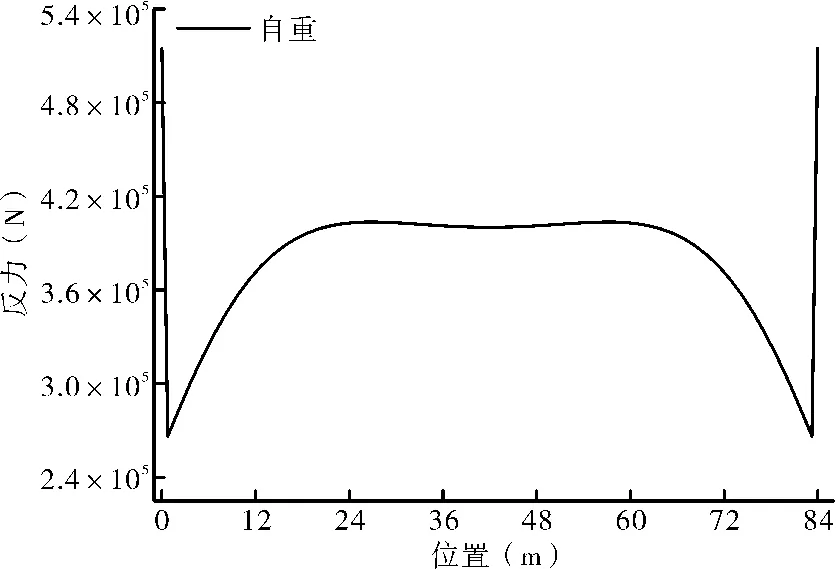
图9 节段预制管廊自重下作用地基反力曲线图
由图9可知,自重作用下,节段预制管廊结构两端面(与现浇位置结合处)受到的水平侧向地基反力最大,距离端面附近地基反力急剧下降,随后侧向地基反力逐渐增大,跨中约3/4区域范围内,水平侧向地基反力基本保持恒定。这是由于节段预制管廊节段之间均采用转动弹簧连接,靠近端面位置处管廊节段之间的转角较大,这在接头弯矩曲线图中也可以看得出来,因此靠近端面位置处水平侧向反力发生较大的变化;管廊结构跨中约3/4区域范围内,由于收到边界条件影响较小,因此水平侧向反力变化幅度不大,基本保持相同。

图10 节段预制管廊自重作用下节段弯矩曲线图
由图10可看出,自重作用下,管廊节段的弯矩呈现以下变化趋势:弯矩以跨中位置对称分布,且出现锯齿状;在距离管廊结构端面位置1/7范围内,管廊节段受到的弯矩逐渐增大,最大值为1.8×106N/m;在1/7跨径至6/7跨径范围内呈现简支梁弯矩变化趋势,最小值为-2.2×105N/m(管廊结构受拉)。受地基土弹簧集中力影响,弯矩曲线图中出现锯齿形状;跨中位置出现的负弯矩表明跨中位置处节段相对于两侧向上拱起,这将导致跨中管廊节段位置出现顶板受拉的情况。
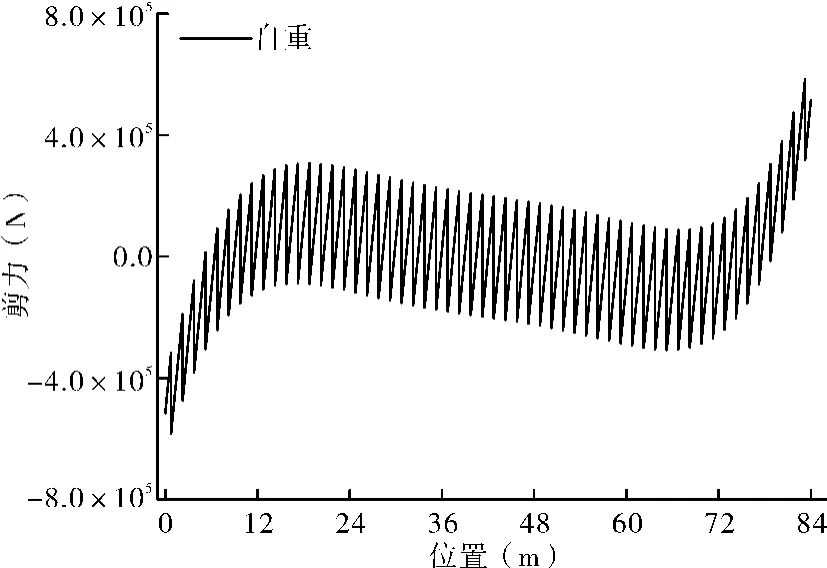
图11 节段预制管廊自重作用下节段剪力曲线图
由图11可看出,自重作用下,管廊节段剪力明显呈现锯齿波动,剪力以跨中为轴反对称分布在1/7跨径至6/7跨径范围内。这是由于提取框架单元内力时是以单元坐标为参考,导致剪力结果出现反对称的现象;受管廊结构两侧边界约束的影响,在两端面(与现浇结合处)出现较大的剪力值。
以上分析结果表明:节段预制综合管廊在自重作用下,跨中位置一定区域内出现管廊顶板部分受拉的状况,因此该位置处顶板部分弹性橡胶垫最先出现弹性压缩减弱,在1/7和6/7跨径范围位置处则会出现底板部分弹性橡胶垫弹性压缩减弱的现象;边界条件的模拟对结构受力影响较大,合理的模拟预制与现浇结合处边界还有待进一步探讨。
3.2 地震作用
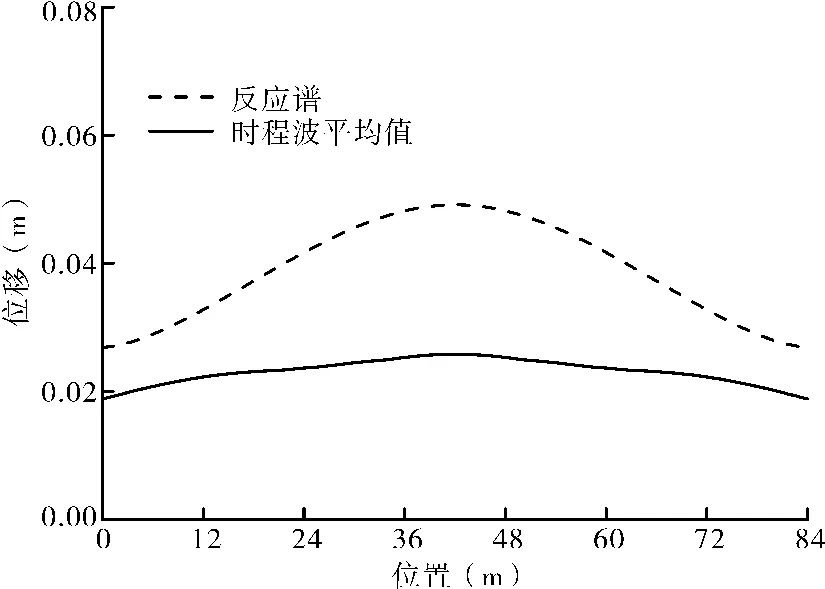
图12 节段预制管廊地震作用下变形曲线图
由图12可看出,在横向地震作用下,管廊结构横向位移的反应谱计算结果和非线性时程计算结果均表现出:跨中横向位移最大,两端面(与现浇结合处)位移最小,两者计算结果变化趋势一致,但反应谱分析结果要较非线性时程计算结果大。这是由于在反应谱计算结果中方向组合采用SRSS法,因此计算结果较非线性时程分析结果偏大;受端面位置边界条件的影响,跨中位移较两侧大。
由图13可看出,在横向地震作用下,整个管廊结构接头弯矩的反应谱计算结果和非线性时程计算结果均表现出:跨中位置接头弯矩最大,1/7跨径范围至2/7跨径范围为平缓过渡段,两侧端面范围内出现陡然下降的趋势。反应谱计算结果较非线性时程计算结果大,原因与位移分析相同,不再赘述。受两侧
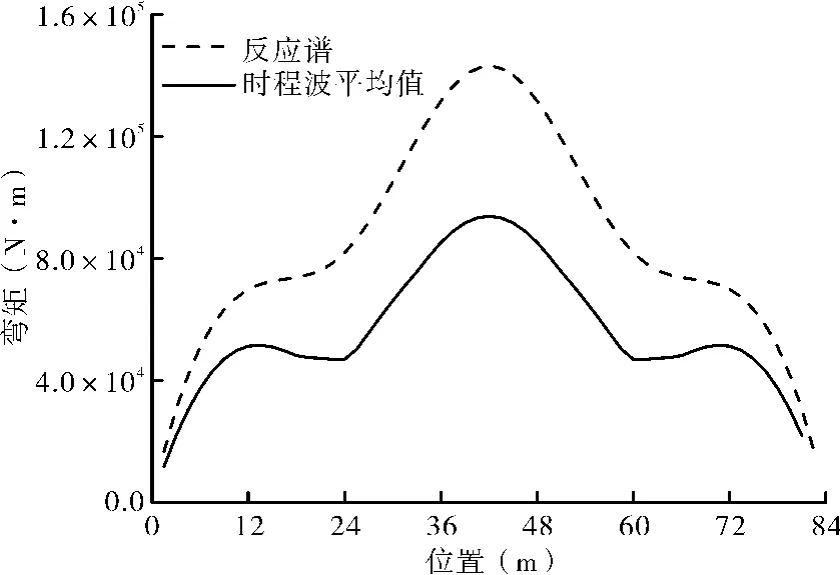
图13 节段预制管廊地震作用下接头弯矩曲线图
边界条件的影响,图14中基础反力变化趋势同自重工况下类似,不再赘述。

图14 节段预制管廊地震作用下基础反力曲线图

图15 节段预制管廊地震作用下节段弯矩曲线图
由图15可看出,地震作用工况下,管廊节段的反应谱计算结果和非线性时程计算结果均表现出:跨中位置附近节段弯矩最大,1/7跨径范围至2/7跨径范围为平缓过渡段,两侧端面范围内出现陡然下降的趋势。其原因分析与接头弯矩分析类似。

图16 节段预制管廊地震作用下节段剪力曲线图
由图16可看出,地震作用工况下,管廊节段剪力沿着长度方向出现波浪形式,具有锯齿形状分布特征,剪力以跨中位置对称分布,两侧端面位置处节段受到的剪力最大,跨中位置处节段受到的剪力最小,但在2/7跨径和5/7跨径位置处出现局部剪力最大。这是由于提取框架单元内力时是以单元坐标为参考,且地震工况下均输出最大值,剪力结果出现对称的现象,这一点和自重工况下不同;受管廊结构两侧边界约束的影响,在两端面(与现浇结合处)出现较大的剪力值。
以上分析结果表明:在地震作用下,节段预制综合管廊反应谱分析结果明显大于非线性时程分析结果,二者结构受力影响变化规律一致。跨中位置附近的接头和节段均为抗震薄弱环节,更容易出现橡胶垫张开甚至漏水的状况,因此采取一定的抗震加固措施显得很有必要,这也是本文分析的重点。预制与现浇结合位置的构造措施将影响着整个结构的内力分布,因此边界条件的合理模拟至关重要。
4 结语
本文针对节段预制拼装综合管廊工程,将管廊节段模拟为梁单元,采用非线性时程分析方法和反应谱分析方法,基于接头刚度模型和等待土弹簧模型进行了节段预制管廊整体抗震性能研究,主要研究结论如下:
(1)自重作用下,跨中区域出现管廊顶板部分受拉的状况,该位置处顶板部分弹性橡胶垫最先出现弹性压缩减弱,在1/7和6/7跨径范围位置处则会出现底板部分弹性橡胶垫弹性压缩减弱的现象。
(2)在地震作用下,节段预制综合管廊反应谱分析结果明显大于非线性时程分析结果,但结构受力影响变化规律一致。
(3)跨中位置附近的接头和节段均为抗震薄弱环节,更容易出现橡胶垫张开导致结构漏水的情况,因此采取一定的抗震加固措施显得很有必要。
(4)预制与现浇结合位置的构造措施将影响着预制拼装部分的受力,也最容易发生剪切破坏,因此很有必要在节段预制拼装和现浇结合处附近对土体采取加固措施,使得土体弹簧刚度不发生突变。
