效能评估可信度的客观度量方法

王军,李建勋,王兴,戚宗锋,3

(1.中国洛阳电子装备试验中心,471000,河南洛阳;2.上海交通大学自动化系,200240,上海;3.电子信息系统复杂电磁环境效应国家重点实验室,471000,河南洛阳)

目前效能评估在装备鉴定、网络安全评估、电力系统性能评估[1]等领域有着广泛的应用。评估可信度是研究评估工作中各环节的可信程度,而目前关于评估可信度研究的公开文献还很少。针对可信度的研究目前大多见于仿真系统,如文献[2-5]分别对重力坝仿真系统、战争模拟系统概率仿真模型、电信网络仿真模型以及移动自组织网络仿真系统的可信度进行了研究。然而,评估系统可信度不同于仿真系统可信度,其主要区别为:①效能评估系统是一个比仿真系统更为抽象的系统,构建仿真系统模型可参考真实系统,而构建效能评估模型无真实模型可以参考;②仿真系统的仿真结果可以与真实系统进行比较,而评估系统无法获取真实值。

效能评估可信度分析可以概括为3个方面:①效能评估过程的可信度分析;②效能评估稳健性实现方法;③效能评估结果可信度分析[6]。在效能评估稳健性实现方法方面,随着机器学习方法的不断发展,大量的研究人员将机器学习算法应用到效能评估中,这在一定程度上解决了效能评估不稳健的问题。在效能评估过程及结果可信度分析方面,文献[7]给出了一种基于元评估的可信度分析方法,该方法通过描述评估过程是否科学严谨,分析评估过程可信度并给出评估结果的可信度结果,本质是一种主观评价方法。评估可信度直接关系到评估结论的使用,只有建立一种效能评估可信度客观度量方法,才能确保效能评估的真正价值。因此,本文研究评估可信度的客观度量方法,解决目前实际工程应用中的问题,以弥补效能评估中的不足。

1 效能评估与模式分类的关系

效能评估流程主要包括评估指标体系构建、指标数据采集、评估模型构建及评估结果分析等[8],如图1所示。在指标体系构建时,要求所选取的每个指标值能描述同类系统不同对象间的区别;在指标数据采集时,通过试验采集相应的指标数据;在评估模型构建时,根据评估工作的需要,建立科学合理的评估模型;在评估结果分析时,通过分析评估结果指导评估工作前面环节的完善。

图1 效能评估主要流程

模式分类是指对表征事物或现象的各种形式信息进行处理,以对事物或现象进行描述、辨认、分类和解释的过程[9]。模式是模式分类系统中的基本元素,根据研究对象的不同,将具有不同特征的对象看作不同的模式,很多问题可以采用模式分类的方法解决,例如故障诊断[10-12]、图像检测[13]等。典型模式分类流程包括数据采集、特征选择或抽取、分类器设计以及分类结果分析[9],如图2所示。

图2 典型模式分类流程

效能评估中的指标选择其实是选择不同的特征,这与模式分类中的特征选择或提取的本质是一样的。如果将不同的效能等级看作不同的模式,那么对被评估对象的效能评估过程也是一种模式分类的过程。因此,为了研究效能评估可信度,本文从模式分类的角度研究评估可信度问题。

2 评估模型可信度

2.1 模型性能评价方法

通过上面的分析可以看出,评估模型实际上可以看作是一个分类模型。对分类模型的性能评价常用的指标是分类准确率、运算速度、成本等,在对效能评估模型性能分析时由于运算速度、成本等本身并不影响分类结果的正确性,因此这里仅考虑模型的分类准确率。

一般在二分类问题中,评价模型分类性能的直观方法是根据正负样本分类结果绘制ROC曲线和AUC曲线[14-15]。在多分类模型中,无正负样本之分,但是仍然可以通过计算分类准确率描述分类模型的性能。多分类模型中,模型对不同类别样本的分类能力是不同的,因此需要分别计算模型对每类样本的分类准确率。第i类样本的分类准确率PTi的计算公式为

(1)

式中:NTi表示i类样本被正确划分的个数;Ni表示i类样本的总个数。

2.2 评估模型可信度

上面从分类的角度给出了评估模型性能评价方法。在评估系统中,模型的可信度代表着评估者对评估模型的认可程度,度量的是一种人主观想法的表现,不同的人对同一模型的认可程度不同,但是人的主观判断是基于客观数据的推断,因此只有基于客观数据通过科学的数学方法得出的可信度才更准确,同时也能够避免不同人对同一模型认可程度不同的问题。

在不确定性理论中,可信度是建立在可能性及必要性测度上的。假设某一事件A发生的可能性测度为Ppos(A),事件A发生的必要性测度为Pnec(A),那么事件A发生的可信度为

C(A)=λPpos(A)+(1-λ)Pnec(A)

0≤λ≤1

(2)

式中:λ为可能性和必要性平衡系数,通常可以认为可能性与必要性同等重要,此时λ=1/2。

本文借鉴不确定性理论中可信度的概念,讨论评估模型的可能性及必要性测度进而确定评估模型的可信度。事件A定义为通过评估模型将应属于A类的样本划分为A类,则事件A发生的可能性测度Ppos(A)定义为事件A发生的概率,即

(3)

式中:PTA表示事件A发生的概率;NTA表示A类样本被正确分类个数;NA表示A类样本总数。

事件A发生的必要性定义为不属于A类的样本被划分到A类的不可能性,于是事件A发生的必要性测度Pnec(A)定义为

(4)

式中:NFA表示不属于A类的样本被错误分为A类的个数;N表示样本总数。

由式(2)～式(4)可以得到事件A发生的可信度为

C(A)=λPpos(A)+(1-λ)Pnec(A)=

(5)

3 单样本分类置信度

对一待测样本,通过分类模型进行分类后,在不考虑分类结果是否正确的情况下,该样本被划分为某类的可信性程度称为单样本分类置信度。单样本分类置信度仅代表模型将样本分类的结果和其相似样本分类结果一致性的度量,与分类结果是否正确无关。例如,样本x1通过某评估模型得到的评估分类结果为y1,模型在对样本x1评估时,经过计算认为x1属于y1的置信度为95%,此时不管分类结果是否正确,样本的评估分类结果置信度就是95%。

关于分类置信度的计算,文献[16-17]给出了一种最近邻分类器的分类置信度计算方法。文献[16]同时给出了SVM分类器分类置信度计算方法。综合各种分类算法的主要思想可知,分类器是通过样本间的距离将进行分类的,这种距离包括同类样本距离与异类样本距离,因此可以通过距离度量样本分类置信度。另外,从高维空间的角度分析,样本在高维空间的分布影响着分类的结果,对单个待测样本来讲,单样本与邻域样本中的同类样本分布关系和异类样本分布关系都影响其分类结果,这些关系包括样本数量和样本空间距离。影响样本分类置信度的因素如图3所示。

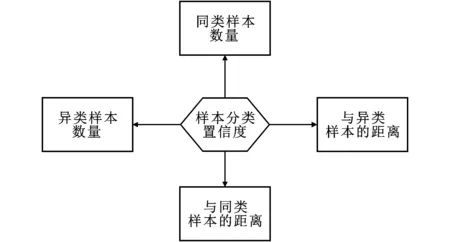
图3 影响样本分类置信度的因素

基于此,本文提出一种新的满足多数分类算法的单样本分类置信度计算方法。

定义1 设ms(x)为测试样本中与待测样本x同类的邻域样本个数,m(x)为测试样本中待测样本x的邻域样本总数,Ds(x)为待测样本x与邻域样本中所有同类样本的欧氏距离和,Dd(x)为待测样本x与邻域样本中异类样本的欧氏距离和。定义待测样本x的分类置信度为

(6)

特别规定:当待测样本邻域内无异类样本时Dd(x)=0。显然,该置信度取值范围是0～1。

4 效能评估综合可信度度量方法

以上分析了评估模型可信度及待测样本置信度,对于待评估的对象,其评估可信度应包括被评估对象样本数据的可信度、模型可信度及样本分类置信度等3个方面。试验数据的可信度主要受试验活动中的不确定性影响,下面讨论试验数据的不确定性对样本数据可信度的影响及处理方法,以及如何将试验数据可信度、评估模型可信度及单样本分类置信度3个方面进行综合,得到最终评估可信度。

4.1 不确定性数据的处理

通常采用随机变量、模糊变量以及区间变量描述试验过程中的不确定性。对于随机变量和模糊变量可以直接计算不确定性测度,进而确定试验数据的可信度,或者将随机变量及模糊变量转化为区间数据再进行处理。文献[18]给出了模糊变量及随机变量的不确定性测度计算方法,本文不再讨论。本文重点研究包含区间变量的评估可信度度量问题。设xi=(xi1,xi2,…,xin)为某装备的试验样本,假设样本分量xi1的值是区间值,即xi1取值范围是a～b。在对样本xi进行效能评估时可以分别采用区间上限及区间下限进行计算,此时计算结果会出现2种情况。一是采用区间上限和区间下限得到的评估分类结果一致,此时区间数据不影响被评估对象的效能等级划分,但是影响效能评估的可信度;二是采用区间上限及区间下限时得到的评估结果不同。进一步假设当取区间上限b时,评估结果为y1,当取区间的下限a时,评估结果为y2,此时需要分别计算该样本属于效能等级y1与y2的可信度。在已知xi1在a～b内的概率密度函数的情况下,假设通过判断xi1取区间中某点c时,样本xi=(xi1,xi2,…,xin)处在分界面上,此时将区间a～b分为a～c和c～b,分别计算a～c及c～b的概率分布值,此时概率分布描述的是仅考虑试验数据时的评估可信度。

4.2 可信度传播模型

设评估系统数学模型为

D=f(X)

(7)

式中:D为评估结果,即效能值;X={x1,x2,…,xn}为评估系统的输入。

可信度传播分为模块间的串联和并联2种情况,可信度传播模型如图4所示。图4a代表的是一种串联情况,其可信度传播模型为

C(D)=C(Y)C[f(X)]

(8)

(a)串联

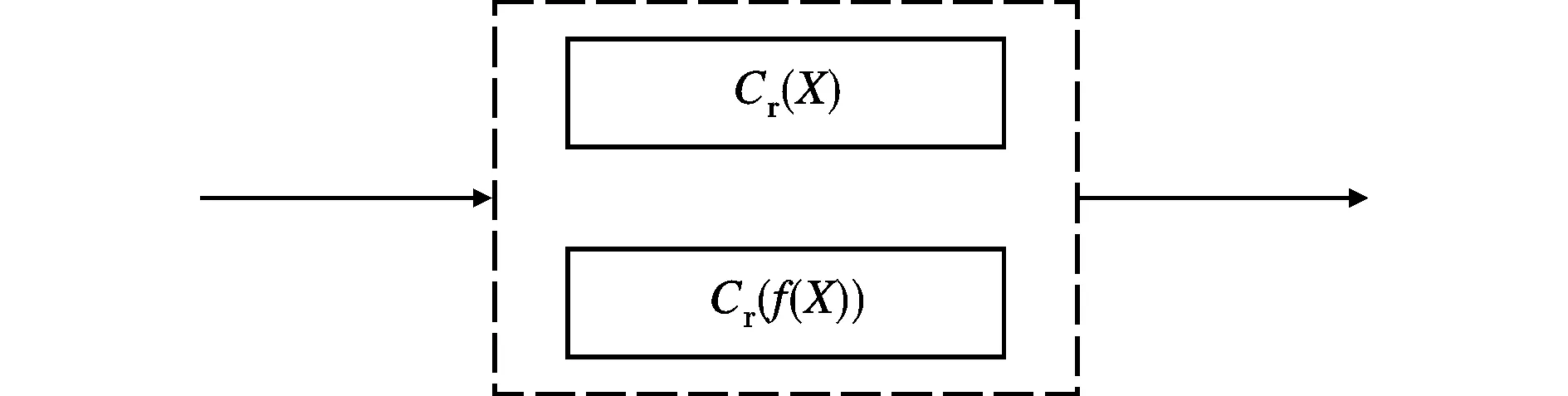
(b)并联图4 可信度传播模型

图4b代表的是一种并联情况,其可信度传播模型为

C(D)=min{C(X),C[f(X)]}

(9)

效能评估可信度是评估数据、评估模型及样本置信度3个因素的累积影响,是一种串联情形。假设试验数据的置信度用Cd(x)表示,模型的可信度用Cm(f)表示,单样本的评估分类的置信度用f(x)表示,那么待评估样本x的综合评估可信度为

C(x)=Cd(x)Cm(f)f(x)

(10)

上面分别讨论了试验数据的不确定性处理方法、评估模型可信度分析方法以及单样本分类置信度计算方法,并给出了一种简单的可信度传播模型。

4.3 综合可信度分析方法原理

从上面的分析可以给出综合效能评估可信度分析方法原理,如图5所示。

图5 评估可信度分析方法原理

从图5可以看出,本文将评估可信度分为评估数据可信度、评估模型可信度以及单样本置信度3个方面。在计算评估数据可信度时,根据所包含的不确定性数据类型,直接计算可信度大小或者转化为区间数据进行处理;在计算评估模型可信度时,将评估模型与模式分类模型建立联系,结合不确定性理论中的可信度概念,将分类性能评价指标转化为可信度指标;在计算单样本分类置信度时,结合现有分类置信度计算的主要思想,综合考虑邻近样本的类别与距离信息,确定待测样本分类置信度。最后,将影响评估可信度的3个方面通过简单的可信度传播模型进行综合,得到最终的评估可信度。

5 实例分析

以雷达抗干扰效能评估为例,选取抗干扰拖引

成功率(P1)、抗假目标欺骗成功率(P2)、发现概率(P3),跟踪误差(E)、抗干扰扇面有效度(θ)以及平局虚假航迹改善因子(I)等6个评估指标。通过仿真试验获取140组数据,将效能等级划分为4个等级(1、2、3、4)得到140个样本的仿真数据,其中部分组数据如表1所示。

选取140组样本中的75组为训练样本、65组为测试样本。将测试样本中效能等级为1的样本集记为S1,共计15个;将效能等级为2的样本集记为S2,共计12个;将效能等级为3的样本集记为S3,共计18个;将效能等级为4的样本集记为S4,共计20个。采用SVM评估模型进行计算,评估程序运行结果界面如图6所示,图中左侧为样本实际分类结果(类标签),右侧是运算错误结果。

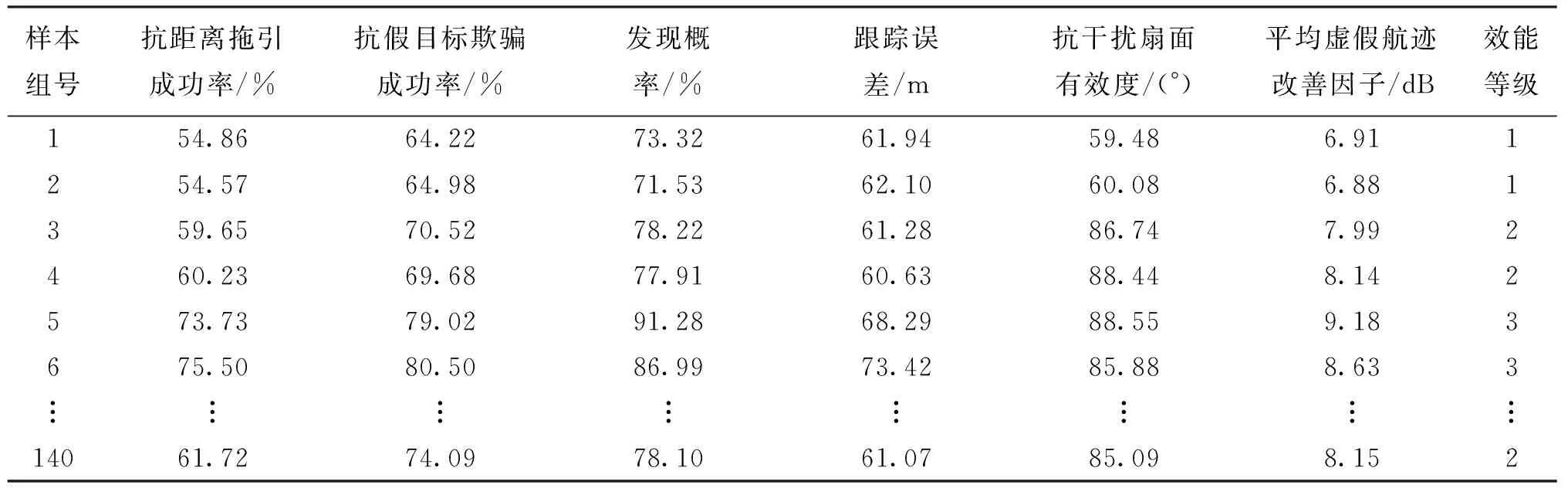
表1 雷达抗干扰效能评估仿真数据

Original Label is:1 Wrongly Predicted Label is 2
Original Label is:1 Wrongly Predicted Label is 2
Original Label is:2 Wrongly Predicted Label is 1
Original Label is:2 Wrongly Predicted Label is 4
Original Label is:3 Wrongly Predicted Label is 2
Original Label is:3 Wrongly Predicted Label is 4
Original Label is:3 Wrongly Predicted Label is 1
Original Label is:4 Wrongly Predicted Label is 2
Original Label is:4 Wrongly Predicted Label is 3
Original Label is:4 Wrongly Predicted Label is 3

图6 评估程序运行结果界面

根据图6的计算结果及式(3)、(4),可得每一类样本分类结果的可能性及必要性分别为

(11)

(12)

根据式(5),取λ=0.5,得到模型对每类样本分类的可信度为

(13)

表2为试验采集的3组待评估装备样本的指标数据,其中部分指标无具体的数据,只能得到其取值的范围。ST2中的θ以及ST3中的I的试验数据是区间值,需要分别考虑区间上限及下限情况,判断其效能等级是否一致。经过分析,ST2中θ取区间上限及下限的效能等级相同。ST3中的指标I取区间下限时,效能等级为3,取区间上限时,效能等级为4,进一步通过区间搜索发现:当ST3中的指标I取值为8.81时,效能等级为3,取值为8.82时,效能等级为4,于是近似认为8.815为ST3样本的效能分界点。假设该参数在区间内取每一点值的概率相同,于是对于样本ST3有:当指标I取值为8.79～8.815时,效能等级为3,其概率大小为0.42;当指标I取值为8.815～8.85时,效能等级为4,其概率大小为0.58。如果想要获取准确的效能等级,需要通过试验进一步确定指标I的精确值。

表2 3组待评估装备试验数据

式(13)给出的模型对每类样本分类可信度在一定程度上描述了评估的可信度。下面进一步分析单样本的置信度。表3给出了测试样本中ST1样本的邻域样本及ST1样本与邻域样本的距离dT1。

由式(6)得到ST1样本的分类置信度为

(14)

记ST2中指标I取区间下限时的样本为ST21,记取区间上限时的样本为ST22,分别计算ST21和ST22的在测试样本中的邻域样本及其与邻域样本的距离dT21、dT22样本,经计算测试样本中ST21和ST22的邻域样本相同,距离信息如表4所示。

由表4及式(6)可以得到T21及T22样本的分类

置信度分别为

(15)

(16)

由式(15)及式(16)的结果可以看出,ST2样本的区间上限和下限结果基本相同,而且效能评估分类结果相同,因此可以忽略指标I的区间数据对ST2样本评估及评估可信度的影响。

对于ST3样本可采用同样的方法进行分析,求得其分类置信度,这里不再赘述。

上面分析了区间数据对评估结果及评估可信度的影响,并得到了模型对每一类样本分类的可信度,同时得到了单样本的置信度。于是,根据串联模块可信度传播模型可以得到样本ST1和ST2的评估可信度为

C(ST1)=C(S2)f(ST1)=0.88×0.68=0.60

(17)

C(ST2)=C(S2)f(ST2)=0.90×0.84=0.76

(18)

式(17)和式(18)表示样本ST1和ST2所代表的装备效能评估结果为等级2和等级3的可信度分别为60%和76%,而3个装备通过蒙特卡洛仿真试验验证的效能等级分别为2、3、4,其可信度分别为0.6～0.68、0.7～0.79以及0.5～0.56。同时,邀请雷达领域4名专家给出的3个装备效能等级分别为2、3、4,其综合可信性分别为0.73、0.86、0.68。

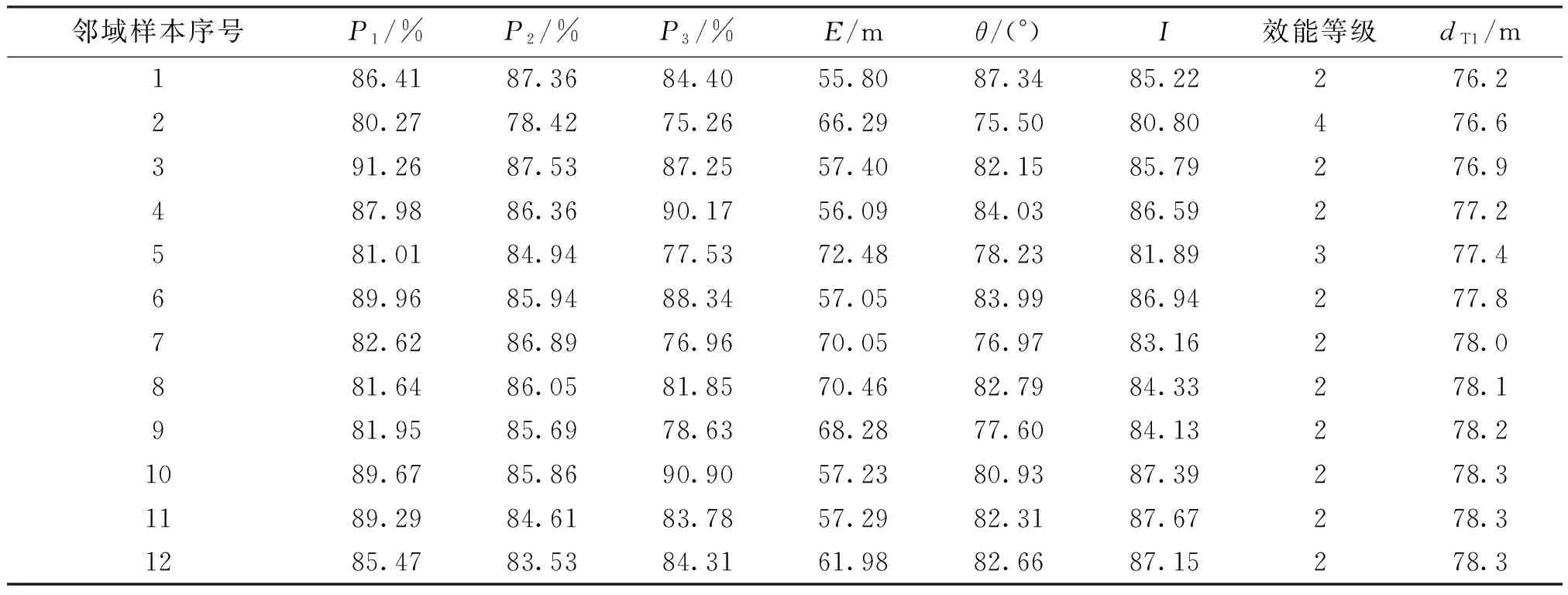
表3 ST1样本的邻域样本及相关数据信息

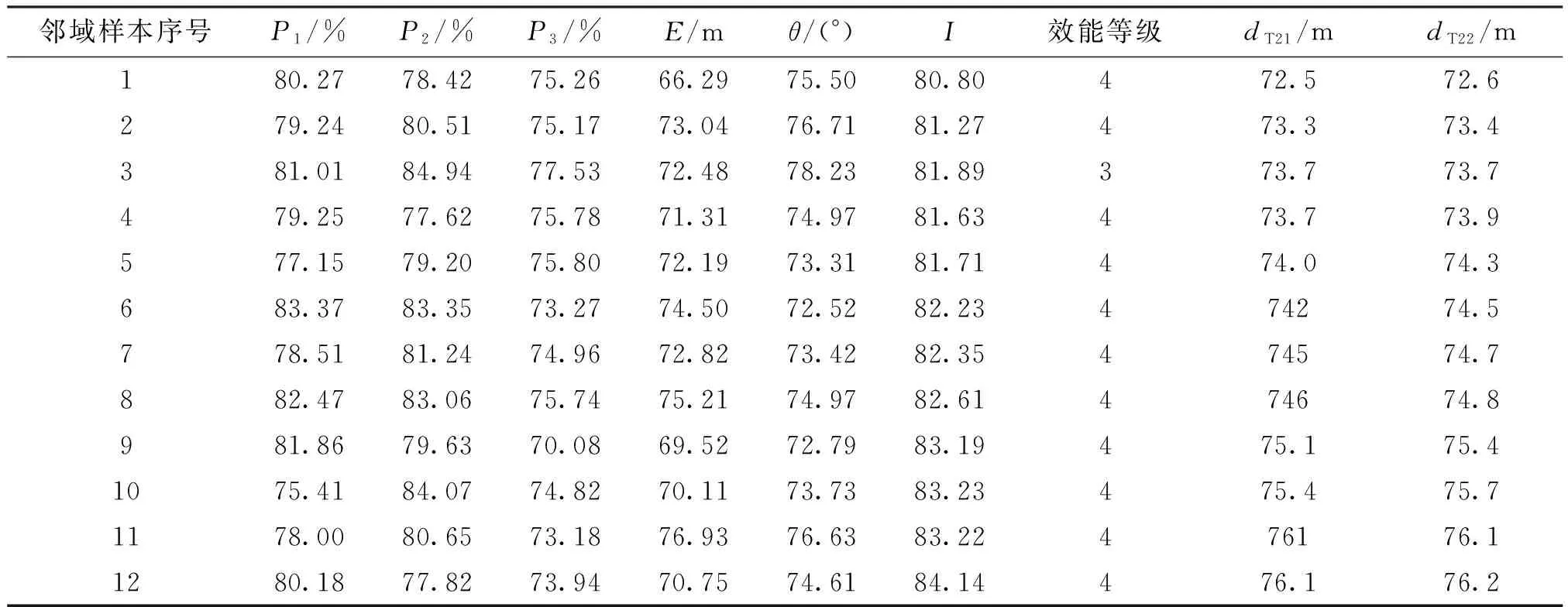
表4 ST2样本的邻域样本及相关数据信息

从上面具体实例可以看出,本文提出的效能评估可信度度量方法并没有利用专家经验知识,避免了不同专家对同一被评估对象评估结果分析的不同,便于编程实现评估结果的自动分析,能够提高计算效率,且计算结果与蒙特卡洛仿真试验结果相符,取蒙特卡洛仿真结果中间值作为可信度基准值,经计算本文方法与专家主观判断结果相比,准确率提高了约10%,证明了本文可信度客观度量方的有效性。

6 结 论

本文为解决评估可信度缺少客观度量方法的难题,在分析现有效能评估与模式分类相关性的基础上,创新性地将模式分类相关理论应用到效能评估中,提出了从试验数据可信度到评估模型可信度,再到单样本分类置信度3个方面客观度量评估可信度的方法。在评估模型可信度分析方面,结合不确定性理论给出了计算评估模型可信度的方法;在单样本分类置信度计算方面,给出了一种适用多数分类算法的相对置信度计算方法;同时本文还讨论了不确定性试验数据对评估可信度的影响及处理方法,并重点研究了区间值数据的处理方法,并给出了一种简单的可信度传播模型,基于可信度传播模型,可得到效能评估综合可信度。最后,以雷达抗干扰效能评估可信性度量为例,验证了本文提出的方法能够在不使用专家经验知识的情况下,客观地度量效能评估可信度,计算结果更加客观、准确,有效地解决了评估可信度难以客观度量的问题,提高了装备试验鉴定效率。

[1] 王秀丽, 张择策, 侯雨伸. 主动配电网多维度静态安全评估 [J]. 西安交通大学学报, 2016, 50(8): 110-116. WANG Xiuli, ZHANG Zece, HOU Yushen. Multidimensional static security assessment for active distribution network [J]. Journal of Xi’an Jiaotong University, 2016, 50(8): 110-116.

[2] CAO X, GU C. Risk analysis of gravity dam instability using credibility theory Monte Carlo simulation model [J]. Springer Plus, 2016, 5(1): 1-14.

[3] 李震, 董鸿鹏, 姜本清. 作战仿真概率模型可信性测试 [J]. 计算机与现代化, 2016(1): 82-86. LI Zhen, DONG H P, JIANG B Q. Credibility test of probability model in warfare simulation system [J]. Computer & Modernization, 2016(1): 82-86.

[4] PAWLIKOWSKI K, JEONG H D J, LEE J S R. On credibility of simulation studies of telecommunication networks [J]. IEEE Communications Magazine, 2002, 40(1): 132-139.

[5] ANDEL T R, YASINSAC A. On the credibility of manet simulations [J]. Computer, 2006, 39(7): 48-54.

[6] 汪连栋, 曾勇虎, 申绪涧. 电子信息系统复杂电磁环境效应研究路线图 [M]. 北京: 国防工业出版社, 2013: 8.

[7] 宋彦学, 张志峰, 齐立辉. 基于元评估的武器装备作战效能评估可信性研究 [J]. 火力与指挥控制, 2009(S1): 128-131. SONG Yanxue, ZHANG Zhifeng, QI Lihui. Research on the creditability of operational effectiveness evaluation with weapon equipment based on meta-evaluation [J]. Fire Control and Command Control, 2009(S1): 128-131.

[8] 黄炎焱. 武器装备作战效能稳健评估方法及其支撑技术研究 [D]. 长沙: 国防科学技术大学, 2006: 22-25.

[9] 姜斌, 黎湘, 王宏强, 等. 模式分类方法研究 [J]. 系统工程与电子技术, 2007, 29(1): 99-102. JIANG Bin, LI Xiang, WANG Hongqiang, et al. Methods for pattern classification [J]. Systems Engineering and Electronics, 2007, 29(1): 99-102.

[10]张西宁, 雷威, 李兵. 主分量分析和隐马尔科夫模型结合的轴承监测诊断方法 [J]. 西安交通大学学报, 2017, 51(6): 1-7. ZHANG Xining, LEI Wei, LI Bing. Bearing fault detection and diagnosis method based on principal component analysis and hidden Markov model [J]. Journal of Xi’an Jiaotong University, 2017, 51(6): 1-7.

[11]WANG T, QI J, XU H, et al. Fault diagnosis method based on FFT-RPCA-SVM for cascaded-multilevel inverter [J]. ISA Transactions, 2016, 60: 156-163.

[12]YIN Z, LIU J, KRUEGER M, et al. Introduction of SVM algorithms and recent applications about fault diagnosis and other aspects [C]∥Proceedings of 2015 IEEE International Conference on Industrial Informatics. Piscataway, NJ, SUA: IEEE, 2015: 550-555.

[13]张鹏, 陈湘军, 阮雅端, 等. 采用稀疏SIFT特征的车型识别方法 [J]. 西安交通大学学报, 2015, 49(12): 137-143.

ZHANG Peng, CHEN Xiangjun, RUAN Yaduan, et al. A vehicle classification technique based on sparse coding [J]. Journal of Xi’an Jiaotong University, 2015, 49(12): 137-143.

[14]张小利. 图像融合及其性能评估若干问题研究 [D]. 长春: 吉林大学, 2016: 115-119.

[15]王颖, 李金, 王磊, 等. 基于机器学习的microRNA预测方法研究进展 [J]. 计算机科学, 2015, 42(2): 7-13. WANG Ying, LI Jin, WANG Lei, et al. Research and progress of microRNA prediction methods on mach in learning [J]. Computer Science, 2015, 42(2): 7-13.

[16]赵行. SVM分类器置信度的研究 [D]. 北京: 北京邮电大学, 2010: 8-20.

[17]薛磊, 杨晓敏, 吴炜, 等. 一种基于KNN与改进SVM的车牌字符识别算法 [J]. 四川大学学报(自然科学版), 2006, 43(5): 1031-1036. XUUE Lei, YANG Xiaomin, WU Wei, et al. An algorithm based on KNN and improved SVM for license plate recognition [J]. Journal of Sichuan University (Natural Science Edition), 2006, 43(5): 1031-1036.

[18]柯宏发, 陈永光, 刘思峰. 电子装备试验数据的不确定性分析方法 [J]. 应用基础与工程科学学报, 2011, 19(4): 653-663. KE Hongfa, CHEN Yongguang, LIU Sifeng. New method of uncertainties analysis for electronic equipment test data [J]. Journal of Basic Science and Engineering, 2011, 19(4): 653-663.