基于Curvelet变换特征的人脸识别算法
2018-02-27杨晋吉李亚文
杨晋吉 李亚文
(华南师范大学计算机学院 广东 广州 510631)
0 引 言
人脸识别技术作为最友好的生物特征识别技术,在国防军事、公共安全、工业和日常生活等方面有着非常广泛的应用,已经得到了广大科学工作者的普遍关注。人脸识别也是模式识别、图像处理、神经网络以及认知科学领域的研究热点和难点[1]。人脸识别主要是将待测的人脸图像与当前人脸库中的图像进行对比,从中找到与之匹配的人脸以达到身份鉴定的目的。目前许多国内外学者对人脸识别进行了深度的研究,总体来说,人脸识别技术目前主要分为以下几类:
1) 基于几何特征的方法。该方法主要是检测出人脸各个关键部位的形状和位置,同时还有这些面部特征之间的关系(比如距离),这些参数就构成了可以表示人脸图像的特征向量。基于几何特征本质上是特征向量之间的匹配,其分量通常包括人脸指定两点间的欧式距离、曲率、角度等。但是该方法从图像中抽取稳定的特征较困难,在表情变化和姿态变化上识别的鲁棒性较差。
2) 基于模板的方法。该方法的关键是利用人脸图像的全局信息或者局部信息,然后选择合适的尺度(如欧几里德距离)与代表人脸信息的标准模板的相关值进行判定。基于模板的方法主要有以下几类:基于相关的方法、特征脸方法(Eigenface[2])、线性判别分析方法(LDA[3])、神经网络方法等。
3) 基于模型的方法。该方法主要是以一种数学模型的变换方法去较好地合并不同姿态、不同角度的人脸信息。其典型方法是Nefian等提出的基于隐马尔可夫模型(HMM[4])的方法,但该方法将同一个人的人脸图像的各种变化看成是同一种状态产生的一系列实现,计算复杂度较高。
近年来,使用变换域去提取人脸特征的方式受到研究人员的广泛关注,而小波变换因其较强的时、频局部化分析能力和多分辨率的特点,被广泛应用于人脸识别当中[5]。然而小波变换的基是各向同性的,仅仅能反映一维信号中奇异点的性质,而无法表达二维图像的“沿”边缘特征,无法最优表示二维图像的奇异曲线,而第二代曲波变换具有对奇异曲线的敏感性而活跃于图像处理领域。李艳萍等[6]提出基于曲波变换和余弦测度人脸识别,周立俭等[7]提出基于Curvelet和LBP的可变光照人脸识别,该方法能够在低分辨率条件下获得较好的识别效果。为了克服小波变换无法准确表示奇异曲线的弱点,本文用Curvelet变换去提取人脸的特征值,利用Curvelet变换后的最优稀疏性去结合稀疏表示分类算法,通过实验本文算法对光照、表情、姿态和遮挡等变化有较好的鲁棒性,同时克服了小波变换无法表达二维奇异曲线的弱点,提高了人脸识别率。
1 曲波变换
1.1 曲波变换理论
Curvelet变换是Candes等于1999年提出的,此时的Curvelet 变换是基于传统结构[8-10], 这种算法结构比较复杂同时具有较高的冗余度。图2表示Curvelet对二维奇异曲线的逼近过程,基的支撑区间为矩形且满足width≈length2,而且这种基还具有很强的方向性,这种关系称之为各向异性尺度关系。对比图1与图2可看出,通过细分后的长条基可以覆盖整个曲线,因此可以看出曲波变换比小波变换对奇异曲线有更优异的表达方式。
曲波变换经过多年的发展目前处于第二代[11],在人脸图像中进行曲波变换则需要使用它的离散形式。本文选取运算速度比较快,算法效率较高的基于Wrapping的快速离散Curvelet变换算法[12],此算法中引入相同间隔的斜率tanθl=l×2-⎣j/2」,l=-2⎣j/2」,…,2⎣j/2」-1,并且定义:
(1)
式中:剪切矩阵Sθl为:
(2)
则离散Curvelet 变换为:
(3)
式中:b∈(k1×2-j,k2×2-j/2)。
基于Wrapping 离散Curvelet 变换算法工作步骤为:
(1) 对人脸图像进行傅立叶变换,可以得到:
(4)
(2) 对于不同角度l和尺度j,产生乘积:
(5)
(3) 对曲波系数的乘积结果进行打包后可以得到:
(6)
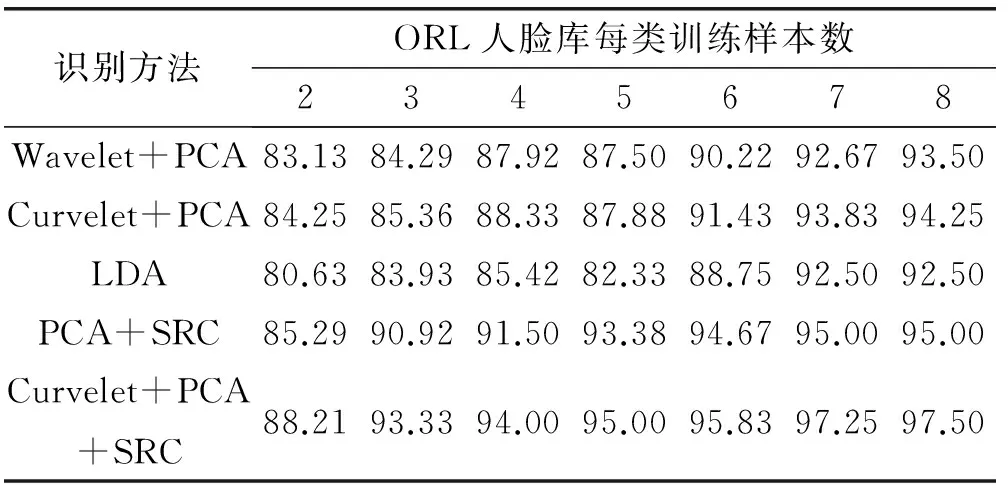
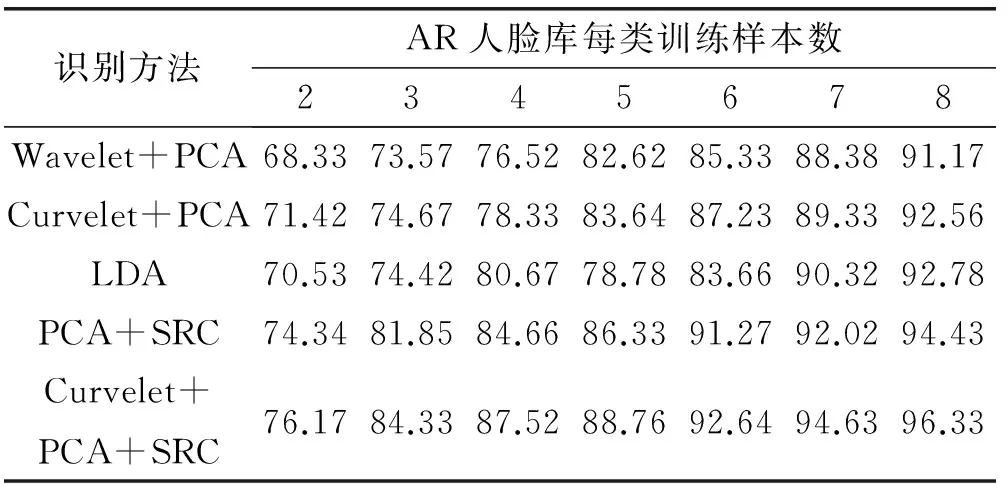
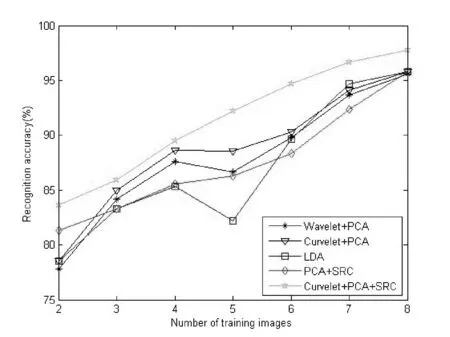
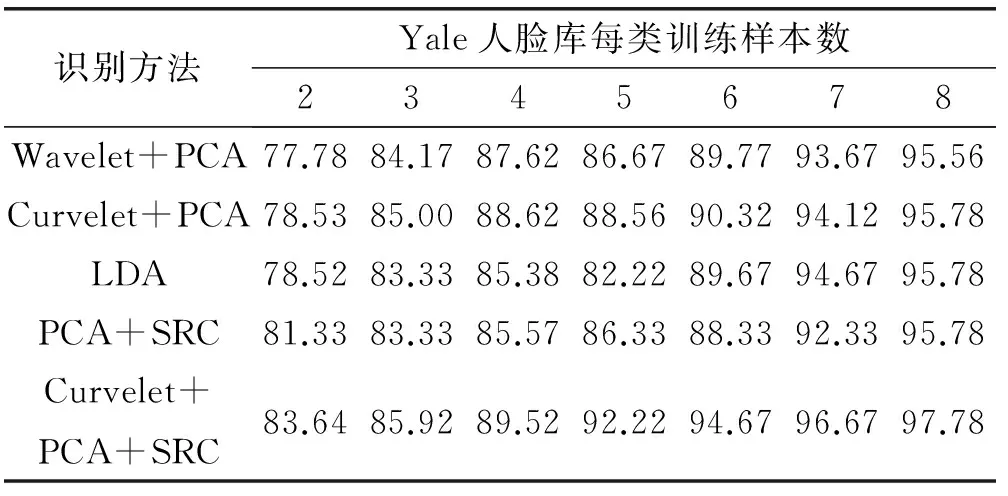
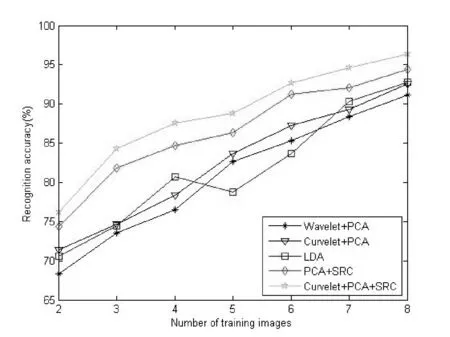
式中:0≤n1 在第二代曲波变换的实现方法上,基本的Wrapping的离散曲波变换主要有如下缺点:人脸的重要图像信息主要位于边缘区域,由于曲波变换时具有平移不变性而导致对分解后的曲波系数的“过扼杀”使边缘区域产生“振铃”效应;曲波变换的基具有“楔形”特性,导致其中的变换因子具有相关性,当曲波变换系数变化时将影响空域中在一条直线上的所有值,导致图像受损。 为了克服该弱点,本实验采用基于第二代曲波的图像加权算法,算法流程如下所示: (1) 使用离散的曲波变换对图像x(i,j)进行分解。 (2) 对分解后的低频和中频曲波系数进行如下非线性变换: (7) 而对于高频曲波系数利用软阈值函数做降噪处理,软阈值函数可以表示如下: (8) (3) 通过曲波反变换获得人脸图像x′(i,j)。 稀疏表示最初常用于信号处理方面,目的主要是用比香农采样定理更低的采样率来表示和压缩信号[13]。当压缩感知理论被Candès[14]首次提出后,稀疏表示理论得到了广泛的应用。近年来Zhou等[15]将稀疏表示和马尔科夫随机场结合起来用来识别部分伪装的人脸;Yang等[16]将Gabor特征加入稀疏表示,不仅提高了人脸的区分能力并且降低了过完备字典的维数。 基于稀疏表示的分类算法(SRC)[17]被成功运用于人脸识别,其核心思想是将测试样本图像表示为训练样本的线性组合,SRC是最经典的针对人脸识别的稀疏表示方法,其基本步骤如下所示: (1) 输入:包含有k个类、n个样本的训练样本集A=[A1,…,Ai,…,Ak]∈Rm×n,测试样本y∈Rm和容错值ε,ε>0。 (2) 归一化列矩阵A使之具有单位l2范数。 (3) 求解最小l1范数: (9) (4) 计算类别i=1,2,…,k的重建误差: (10) (5) 输出重建误差最小的类作为测试样本y的类: identity(y)=argminiri(y) (11) 本文采用Curvelet 变换获取人脸特征,在实现方法上采用改进的Wrappinp快速离散Curvelet 变换加权算法,结合PCA降维后用稀疏表示分类算法SRC进行识别(如图3所示),其主要步骤如下: (1) 图像预处理,主要通过对图像的灰度化和归一化处理来保证提取有效的人脸特征。 (2) 离散Curvelet变换,采用本文改进的曲波变换加权算法对训练集图像和测试集图像进行分解和重构,取得对应的低频子带部分和不同方向和尺度的高频子带部分,对低频系数重构图像(即曲波脸)作为人脸的特征矩阵。 (3) PCA降维,为了降低运算复杂度得到维数低的稀疏特征,则采用PCA方法对训练集和测试集的特征矩阵进行降维。 (4) SRC分类识别,对经过降维后的训练集和测试集特征用稀疏表示分类算法(SRC)进行人脸识别。 图3 本文算法流程图 为了验证本文算法的有效性,分别在ORL、Yale和AR三个人脸数据库进行实验,并与基于Wavelet变换的PCA算法、基于Curvelet变换的PCA 算法、LDA、PCA+SRC进行比较。实验软件平台为MATLAB 2014a,硬件为i5-5200U 处理器,主频为2.20 GHz,4 GB内存,Windows7(64)位操作系统。实验过程中需要用到三个工具箱,分别为Libsvm、CurveLab、PhDtool。 本实验选取了ORL、Yale和AR人脸数据库进行实验。ORL人脸库由剑桥大学AT&T实验室创立,共有40个人一共400幅灰度图像组成,其中包括表情变化,微小姿态变化,20%以内的尺度变化,如图4所示。Yale人脸库由耶鲁大学计算视觉与扼制中心创立,包括15位志愿者的165张图片,包括光照,表情和姿势的改变,如图5所示。AR人脸数据库由西班牙巴塞罗那计算机视觉中心建立,包含116人的3 288幅图像,包括遮挡,表情和姿势的改变,如图6所示。 图4 ORL人脸库样本图像(姿态、表情、尺度变化) 图5 Yale人脸库样本图像(光照、表情变化) 图6 AR人脸库样本图像(遮挡、光照、表情变化) 根据三个人脸数据库各自的特点,本仿真实验在人脸姿态、表情、尺度变化上选择ORL人脸库进行实验,在光照、人脸表情变化上用Yale人脸库进行实验,在人物遮挡、光照、表情变化上用AR人脸库进行实验。第一个实验选用ORL人脸库中的每个人作为一个类别,然后每类训练样本数为x(2~8),表1是各种识别算法在ORL人脸库的识别率。 表1 ORL人脸库在不同算法的识别率比较 从表1实验数据表明,在表情变化,姿态变化,尺度变化的人脸识别中,本文采用的人脸识别算法有比较好的人脸识别效果。 本文算法与传统的基于Wavelet变换的PCA算法、LDA相比较有明显识别性能提高,在训练集的个数依次递增的过程中本文算法识别效果显著。本实验设置了曲波变换和小波变换的对比实验,如图7所示,基于曲波变换的PCA识别算法要比基于小波变换的PCA算法的识别效率高一些。这也验证了小波变换无法准确表示人脸图像奇异曲线的弱点,对含有较多面部轮廓和五官曲线信息的人脸图像无法实现最优的稀疏表示。而本文算法将人脸图像在经过Curvelet变换后与稀疏表示类识别算法结合具有较高识别率,这是因为人脸图像经过Curvelet变换后具有优秀的稀疏性。为了充分证明本文识别算法在姿态变化、光照变换、表情变化上的良好识别率,也在Yale人脸库中进行了相关实验,表2是各种识别算法在Yale人脸库的识别率。 图7 ORL人脸库不同算法识别率(姿态、表情、尺度变化) 识别方法AR人脸库每类训练样本数2345678Wavelet+PCA68.3373.5776.5282.6285.3388.3891.17Curvelet+PCA71.4274.6778.3383.6487.2389.3392.56LDA70.5374.4280.6778.7883.6690.3292.78PCA+SRC74.3481.8584.6686.3391.2792.0294.43Curvelet+PCA+SRC76.1784.3387.5288.7692.6494.6396.33 由表2实验数据表明,在光照变化,表情变化,姿态变化的人脸识别中,本文算法识别效果也普遍高于其他对比算法。从图8可知,经过Curvelet变换后的PCA识别算法识别率略高于基于小波变换的PCA识别算法,可见在某些人脸库中基于小波变换类的识别算法和基于曲波变换类的识别算法的基本识别率相差不是太大。这也从侧面反映了人脸图像经过曲波变换后进行非稀疏表示类识别算法识别人脸效果甚微。而PCA+SRC算法的识别效率低于经过曲波变换的PCA+SRC算法,这是因为包含众多曲线信息的人脸图像经过Curvele变换后拥有最优的稀疏表示,此时结合稀疏表示分类算法识别效果显著。 图8 Yale人脸库不同算法识别率(光照、表情变化) 为了验证本文算法在遮挡、表情变化和光照变化下的有效性,本文采用AR人脸数据库进行测试。AR人脸数据库包括人脸遮挡,人脸表情和姿势的改变。原AR人脸库每个人有26幅不同的人脸图像,为了实验公平性,我们选取每个人的偶数编号图片进行实验并且重新编号,表3是各种识别算法在AR人脸库的识别率。 表3 AR人脸库在不同算法的识别率比较库不同算法识 由表3实验数据表明,在人脸遮挡,光照变化,表情变化的人脸识别中,本文算法识别效果也普遍高于其他对比算法。从图9可知,在遇到人脸遮挡和表情变化的情况下,基于小波变换的PCA和LDA人脸识别算法的效率不及本文算法的识别效率。基于小波变换的PCA识别算法和经过Curvelet变换的PCA识别算法的识别率非常接近。这也验证了之前的结论:经过Curvelet变换与其他非稀疏表示方法结合效果甚微,而经过Curvelet变换对稀疏表示类的人脸识别算法有提升识别率的作用。 图9 AR人脸别率(遮挡、光照、表情变化) 本文提出的基于Curvelet变换特征的人脸识别算法对于人脸识别有较好的识别效果。本文算法既克服了在人脸识别中小波变换无法准确表示奇异曲线的弱点,也增强了在外界干扰因素下的人脸识别效率。算法采用本文改进的Wrappinp快速离散Curvelet 变换加权算法获得人脸的稀疏特征,具备稀疏性的人脸特征通过降维后采用稀疏表示分类算法进行人脸识别。通过在ORL人脸数据库、Yale人脸数据库和AR人脸数据库上的相关对比实验,证明了本文算法在人脸遮挡、姿态变换、表情变换和光照变换等干扰因素的作用下具有较高的人脸识别率和较好的鲁棒性。但是本文算法也在人脸识别阶段经过了多次人脸特征变换,为保证在大数据的情况下有较高的识别率及快速的识别能力也是将来要研究的方向之一。而基于稀疏表示的人脸识别改进算法都要求人脸特征必须在识别分类前严格对齐,这一点限制了稀疏表示识别算法的实际应用场景。 [1] 李昆仑,耿雪菲,曹静媛.鉴别稀疏保持投影的人脸识别算法[J].小型微型计算机系统,2017(2):376-380. [2] Lades M,Vorbruggen J C,Buhmann J,et al.Distortion Invariant Object Recognition in the Dynamic Link Architecture[J].IEEE Transactions on Computers,1993,42(3):300-311. [3] Huang R,Liu Q,Lu H,et al.Solving the small sample size problem of LDA[C]//16 Th International Conference on Pattern Recognition.IEEE Computer Society,2002:30029. [4] Baum L E,Eagon J A.An inequality with applications to statistical estimation for probabilistic functions of Markov processes and to a model for ecology[J].Bulletin of the American Mathematical Society,1967,73(3):360-363. [5] Amira A,Farrell P.An automatic face recognition system based on wavelet transforms[C]//IEEE International Symposium on Circuits and Systems.IEEE,2005:6252-6255 Vol.6. [6] 李艳萍,姜颖,胡金明,等.基于曲波变换和余弦测度的人脸识别方法[J].计算机科学,2016,43(5):294-297. [7] 周立俭,刘万泉,孙洁.基于Curvelet和LBP的可变光照人脸识别[J].计算机工程,2012,38(22):176-178. [8] Mandal T,Majumdar A,Wu Q M J.Face Recognition by Curvelet Based Feature Extraction[M]//Image Analysis and Recognition.Springer Berlin Heidelberg,2007:806-817. [9] Candès E J,Donoho D L.New tight frames of curvele ts and optimal representations of objects with smooth singularities[J].Communications on Pure & Applied Mathematics,2004,57(2):219-266. [10] Lee C S,Pan C Y.An intelligent fuzzy agent for meeting scheduling decision support system[J].Fuzzy Sets and Systems,2004,142(3):467-488. [11] 宋书林,张彦,王宪,等.基于曲波变换和Retinex人脸光照处理算法[J].计算机工程与应用,2013,49(3):171-173. [12] Candes E,Donoho D,Demanet L.Methods for performing fast discrete curvelet transforms of data:US,US 7840625 B2[P].2010. [13] Donoho D.Compressed sensing[J].IEEE Transactions On Information Theory,2006,52(4):289-1306. [14] Candès E J.Compressive sampling[C]//Proceedings of the International Congress of Mathematicians.Madrid,Spain,2006:1433-1452. [15] Zhou Z,Wagner A,Mobahi H,et al.Face recognition with contiguous occlusion using Markov random fields[C]//2009 IEEE 12th International Conference on Computer Vision,2009:1050-1057. [16] Yang M,Zhang L,Shiu S C K,et al.Gabor feature based robust representation and classification for face recognition with Gabor occlusion dictionary[J].Pattern Recognition,2013,46(7):1865-1878. [17] Wright J,Yang A,Ganesh A,et al.Robust face recognition via sparse representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI),2009,31(2):210-227.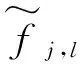
1.2 改进的曲波变换加权算法
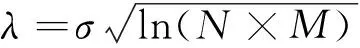
2 基于稀疏表示分类的人脸识别
2.1 稀疏表示分类识别
2.2 本文算法

3 实验结果及分析




4 结 语
