场地波速结构对地表地震动估计影响分析

朱冰清 赵黎明 李恩建 徐诚 李颖楠 姜海

摘要

本文為了得到场地波速结构对地表地震动的影响，选取了1个具有代表性的钻孔，属于Ⅱ类场地，选用天然记录的地震波埃尔森特罗波作为基底入射波，建立一维土层地震危险性分析的计算模型，同时，将两条天然波的地震动水平加速度值调整为50gal、100gal、150gal、200gal、300gal和500gal，并分别调整两次土层顺序，最后利用soil程序对选取的Ⅱ类场地钻孔资料进行场地地震危险性分析，并对得到的结果进行对比分析。

【关键词】工程场地波速结构地震动

地震是地球内部介质局部发生急剧破裂，产生的地震波，从而在一定范围内引起地面震动的现象。地震简直是无法抗御的。但是经过一个多世纪的地震工程研究工作表明，人类虽然无法阻止地震灾害的发生，但是我们可以采取适当的措施，使地震灾害尽可能的减轻。

场地条件作为影响震害的主要因素之一。场地条件一般指局部地质条件，如近地表几十米至几百米内的地基土壤、地下水位等工程地质情况、地形及断层破碎带等。国内外震害经验一致表明场地条件是震害或地震烈度的主要影响因素，且早在1906年旧金山大地震中人们己认识到这种影响。

规范中的场地类别划分方法为20米内场地覆盖土层厚度以及等效剪切波速。一般都认为同一类别土中，在同一地震反应下，对地表地震动特性具有相同或相似的影响。但是土层结构改变后，会对地表地震动有影响。

所以，此论文的主要工作是研究同一场地，在相同的地震反应中，土层结构改变后，对地表地震动加速度、速度、位移峰值和反应谱加速度最大值有多大的影响。选取天然地震动作为基岩输入地震动，选取Ⅱ类场地作为原始土层反应模型，改变土层顺序，共组合了21种不同工况模型，进行了场地地震反应分析。

1 一维土层地震反应分析方法

一维模型是一种半无限弹性均匀基岩空间上覆盖水平成层土体的较为理想的场地力学模型。它是假定土层沿两个水平方向均匀无变化，而仅沿竖向分层变化。虽然一维场地模型是一种较为简单的场地力学模型，但从工程近似的角度来说，基于这一模型的场地地震反应分析方法能够反应局部范围内地面、土层界面及基岩面较平坦的场地对地震动影响的主要特征。因此，对于大多数局部场地或大面积场地，如城市区划场地，采用简单的一维场地力学模型进行土层的地震反应分析己能满足工程应用要求。

本文的主要目的就是应用一维土层地震危险性分析模型，输入典型钻孔地质剖面资料和基底入射波，并应用这一模型计算出场地土的动力参数特性、地表加速度、地震反应谱等特征进行对比分析，为建筑物的抗震设计提供参数。

2 数据的选取

2.1 输入地震动

本文选用埃尔森特罗地震记录作为基底入射波，以反映输入地震动特性对场地地震效应的影响。同时，将埃尔森特罗波地震动峰值水平调整为50gal、100gal、150gal、200gal、300gal、500gal利用程序soil对Ⅱ和Ⅲ类场地进行一维土层地震危险性分析。

2.2 场地钻孔资料

本文分别从Ⅱ类中各选取了一个典型的场地钻孔资料（如表1）。之后变换土层顺序，第一次将原始土层的第1层换到8层，原始土层第8层厚度为2.9m，而第一层为1.85m，因此将原始土层的第8层分为两小层，上半层为原始土层的第1层，厚度为1.85m;下半层为原始土层的第8层，厚度为1.05m。第二次将原始土层的第1层换到4层，原始土层第4层厚度为2.55m，而第一层为1.85m，因此将原始土层的第4层分为两小层，上半层为原始土层的第1层，厚度为1.85m，下半层为原始土层的第4层，厚度为0.7m.

2.3 Ⅱ类场地土的动剪切模量比和阻尼比

根据上述Ⅱ类钻孔资料，一维土层地震反应计算程序中用到的土的动力特性参数如表2所示，参考田启文[1]书中的各类土的动剪切模量比和阻尼比的表，这些参数在运行程序时将作为输入文件data3的数据。

3计算结果与分析

3.1 原始土层地表反应、第一次变动土层地表反应及第二次变动土层地表反应

具体做法：以埃尔森特罗地震波作为基底入射波，原始土层场地钻孔资料为例。

（1）根据已知条件建立并修改输入数据文件DATA.dat、DATAl.dat、DATA2.dat、DATA3.dat、DATA4.dat;

（2）运行执行程序（Rsleibm）得出五个输出文件rtell.dat，rtel2.dat，rtel3.dat，rte14.dat，rtel5.dat，经过查找文件rtell.dat可以得出Amax，Vmax，Dmax的值;

（3）运行ARTELTR程序，得到3个输出文件，分别为Aco-1.dat、Acc-2.dat、Acc-3.dat，其中Acc-1.dat是用来做时程图的文件;

（4）运行RTELTR程序，得到3个输出文件，分别为Res-1、Res-2、Res-3，其中Res-1是用来做反应谱曲线的文件;

（5）对soil程序输出的加速度时程图文件，运用matlab软件进行滤波处理，并计算出速度和位移时程图文件。

（6）最后在Excel表中分别画出各个埃尔森特罗地震波在土层变换前后的加速度、速度和位移时程图以及反应谱曲线对比。

3.2 场地计算结果分析

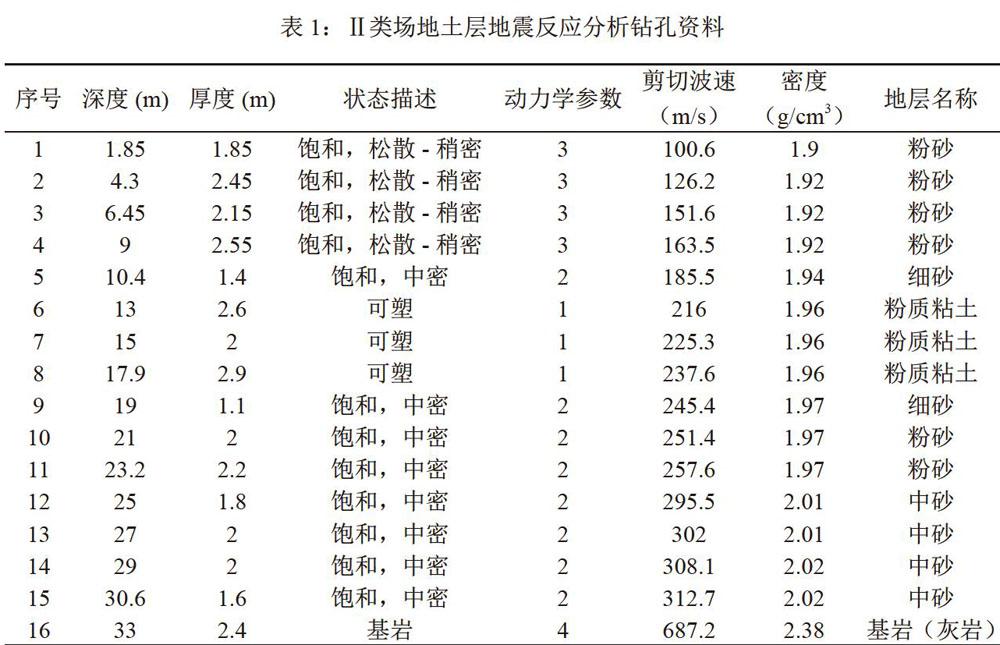
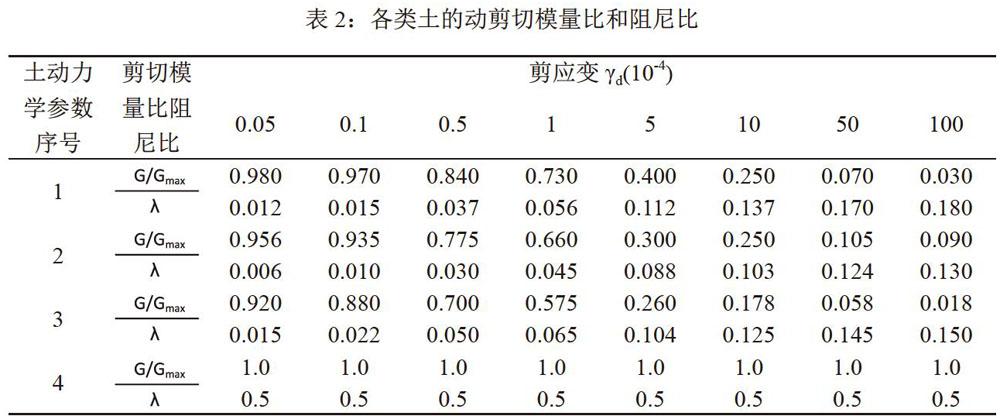
计算时，将Ⅲ类场地的软土层（第一个土层，波速为100.6m/s的粉砂层）分别变换到第八层（波速为237.6m/s的粉质粘土层）和第四层（波速为163.5m/s的粉砂层），即将第一次将软土层变换的深，第二次将软土层变换的浅。在七种不同的埃尔森特罗地震动的输入作用下共进行了21种工况的工程场地地震危险性分析。不同输入加速度水平下的土层变换的反应谱曲线如图1、2所示。

从图1-2的不同输入加速度水平下的土層变换的反应谱曲线中可以看出，变换土层顺序、输入地震动特性以及地震强度的不同，都对Ⅱ类场地的加速度反应峰值Amax、特征周期Tg以及反应谱最大值Samax有一定的影响，并且存在一定的规律性：

（1）从图1-2可知，变换土层前后，反应谱曲线形状相似，大小不一样。

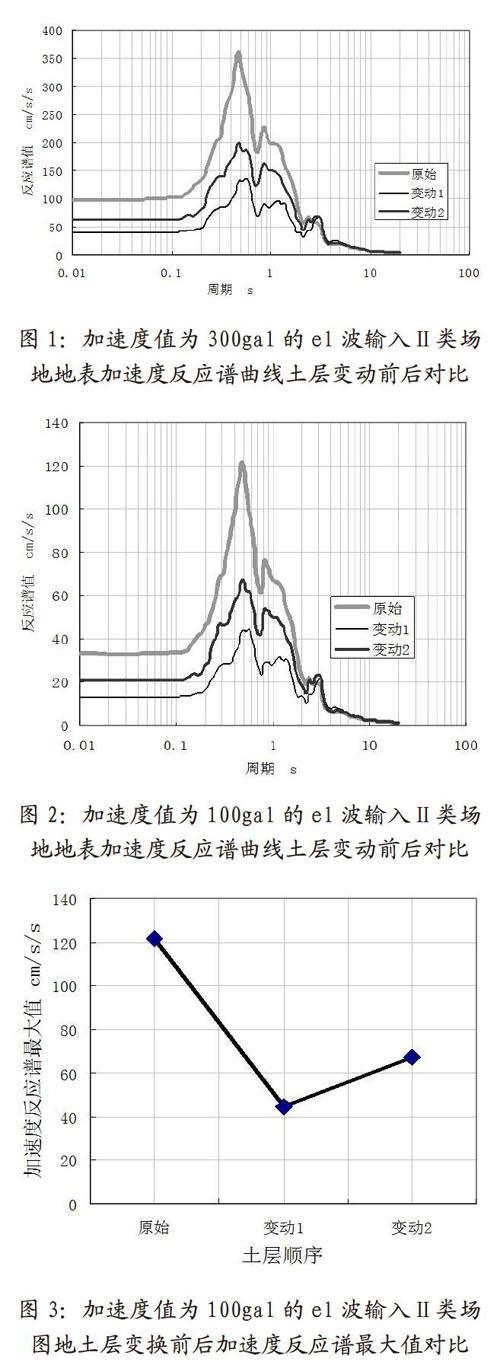
（2）如图3所示，在加速度值为100gal的埃尔森特罗地震动的输入作用下，第一次变换土层顺序与第二次变换土层顺序相比，软土层变换的深的比变换的浅的加速度反应谱最大值小且都比原始土层的加速度反应谱最大值小。通过对比分析，在不同地震动输入作用下土层变换前后反应谱加速度最大值对比，如图4所示，可以看出在同一输入地震动作用下，第一次变换土层顺序与第二次变换土层顺序相比，软土层变换的深的比变换的浅的加速度反应谱最大值小，且随着基底入射波加速度值的增大，加速度反应谱最大值也逐渐增大。

（3）在加速度值为50gal的埃尔森特罗地震动的输入作用下，第一次变换土层顺序与第二次变换土层顺序相比，软土层变换的深的比变换的浅的特征周期值大且都比原始土层的特征周期值大。通过对比分析，在不同地震动输入作用下土层变换前后特征周期值对比，可以看出在同一基底入射波作用下，第一次变换土层顺序与第二次变换土层顺序相比，软土层变换的深的比变换的浅的特征周期值大，且都大于原始土层的特征周期值;随着基底入射波加速度值的增大，特征周期值基本不变。

（4）同一土层，在不同的埃尔森特罗地震动作用下，加速度反应谱最大值所对应的周期相同。

（5）同一埃尔森特罗地震动作用下，土层顺序改变前后，软土层变换的深的土层比软土层变换的浅的土层峰值加速度小，且都小于原始土层的峰值加速度。

（6）同一土层，在不同的埃尔森特罗地震动作用下，随着基底入射波加速度值的增大，峰值加速度逐渐增大。

（7）同一埃尔森特罗地震动作用下，土层顺序改变前后，软土层变换的深的土层与软土层变换的浅的土层峰值速度基本相同，都略小于原始土层的峰值速度。

（8）同一土层，在不同的埃尔森特罗地震动作用下，随着基底入射波加速度值的增大，峰值速度逐渐增大。

（9）同一埃尔森特罗地震动作用下，土层顺序改变前后，土层峰值位移基本相同。

（10）同一土层，在不同的埃尔森特罗地震动作用下，随着基底入射波加速度值的增大，峰值位移逐渐增大。

（11）结构变动后土层的Samax和未变动前土层的Samax，二者之间的比值随着输入el波加速度峰值的增加基本不变。

5 结论

本文以实际场地钻孔资料为基础，挑选了1个典型的场地剖面，以场地波速结构为基准，分别变换了两次土层顺序，选用埃尔森特罗地震波的加速度记录作为基底入射波，并考虑输入地震动强度的影响，调整输入地震动的加速度值，利用soil程序共进行了21种不同工况的数值计算，分析了场地波速结构对地表地震动的影响，并归纳了一些规律。通过上述分析，可得到以下结论：

（1）同一土层结构，输入地震动强度不同，特征周期值不变。

（2）在同一地震动输入作用下，土层结构改变后，反应谱形状相似，大小改变。

（3）同一土层结构，输入的地震动强度越大，Amax、Vmax、Dmax、Samax越大。

参考文献

[1]田启文.工程地震学基b} [M].地震出版社，2009.

[2]吕悦军，彭艳菊，兰景岩，孟小红.场地条件对地震动参数影响的关键问题[J].震灾防御技术，2008.

[3]赵艳，郭明珠，季杨，王文仲，张玫.场地条件对地震动持时的影响[J].震灾防御技术，2007.

[4]陈继华，陈国兴，史国龙.深厚软弱场地地震反应特性研究[J].防灾减灾学报，2004（06）.

[5]陈国兴，陈继华.地震动输入界面的选取对深软场地地震效应的影响[J].世界地震工程，2005（06）.

[6]陈国兴，谢君裴，张克绪.土的动模量和阻尼比的经验估计[J].地震工程与工程振动，1995（15）.

[7]吴世明.土动力学[M].北京：中国建筑工业出版社，2000.

[8]李小军.粘弹塑性模型及土层地震反应分析[D].哈尔滨：国家地震局工程力学研究所，1987.

[9]李小军，彰青等.设计地震动参数确定中的场地影响考虑[J].世界地震工程，2001.

[5]李小军，彭青等.不同类别场地地震动参数的计算分析[J].地震工程与工程振动，2001.

[10]周克森.一维土层非线性地震反映分析方法[J].地震工程与工程振动，1996.