振荡翼型气动及其噪声特性的数值研究

郭艳丽+马尊领+陈二云+杨爱玲

摘 要： 针对低雷诺数下翼型的非定常气动噪声特性，采用计算流体力学（CFD）与Lighthill声类比相结合的方法，分别对俯仰、平振以及俯仰与平振耦合运动的翼型进行了分析，通过自定义程序控制翼型的运动规律，并对其流场及诱导的声场特性进行了数值仿真.结果表明：随着折合频率、振幅的增加，翼型表面升力系数的峰值增大，非定常迟滞效应增强；耦合运动的相位差改变了气动力的响应特性；对于振荡翼型激发的噪声，低频下单极子声源占主要地位；随着声源频率的增大，远场声压指向性逐渐体现出偶极子声源的特性.

关键词： 振荡机翼； 折合频率； 气动噪声； 指向性曲线； Lighthill声类比

中图分类号： O 355 文献标志码： A

Abstract： The combination of computational fluid dynamics（CFD） and Lighthill acoustic analogy was applied to analyze the unsteady aerodynamic noise characteristics of oscillating airfoil at low Reynolds number.The unsteady performance of the airfoil was studied under the conditions of pitching，flapping and the coupling oscillation，respectively.The airfoil movements were controlled using custom program.The results showed that with the increasing of reduced frequency and amplitude，the peak value of lift coefficient in the airfoil surface increased.So did the unsteady hysteresis effect.The phase differences of coupling oscillation changed the aerodynamic characteristics.For the noise excited from oscillating airfoil，it was predominantly the monopole source.With the rising of the sound source frequency，the farfield sound pressure directivity had a trend towards to dipole source.

Keywords： oscillating airfoil； reduced frequency； aerodynamic noise； directivity curve； Lighthill acoustic analogy

隨着微型飞行器和水下航行器的出现，低雷诺数下翼型的气体动力学特性愈发受到关注.这类飞行器的运动通常经历不稳定的状态，如平振和俯仰.研究[1-2]发现，在相同的流场条件下，做振荡运动的翼型要比静态翼型能产生更高的升力，失速迎角也增加，特别是振荡翼型绕流的涡脱落特性及其诱导的气动噪声与静态翼型诱导的噪声有较大区别.因此，关于振荡翼型气动及其诱导的噪声特性的研究对提高飞行器的气动效率和降噪方面都有十分重要的意义.

气动噪声是非定常流动的必然结果，因此，直接求解非定常N-S/Euler方程获得流场与声场解是最符合物理本质的方法.但是，声场的非定常性、声学物理量的小量级及声波传播的特性对数值离散格式、计算网格和边界条件都提出了很高的要求，使得声场直接模拟方法受到极大的制约，应用于工程实际还需时日.因此，基于计算流体力学（CFD）和Lighthill声类比相结合的方法是目前求解气动噪声的主要手段[3].

目前关于振荡翼型气动特性的研究较丰富，但对于振荡翼型气动噪声的研究相对较少.例如：文献[4-6]通过风洞实验对翼型作俯仰振动时的动态失速特性进行了研究；Jung等[7]研究了振荡翼型尾迹区涡脱落特性受来流攻角和相位角的影响特性；史志伟等[8]、姚迪等[9]研究了振荡翼型表面的压力分布和升力系数与翼型振荡频率和振荡幅值之间的关系；杨爱玲等[3]结合非定常流场计算程序与Kirchhoff积分程序对翼型做俯仰运动时诱发的远场噪声进行数值预测，获得了远场观察者的瞬时声压和声场指向性分布.

鉴于上述原因，本文采用CFD和Lighthill声类比相结合的方法，以NACA0012翼型为对象，研究低雷诺数下振荡翼型的气动及其诱导的噪声特性，重点分析该翼型在俯仰、平振以及俯仰平振耦合运动下的噪声水平和指向性分布.

1 计算模型及方法

振荡翼型具有很强的非定常和非线性特点，必须通过求解不可压N-S方程模拟该现象.求解时，控制方程对流项采用二阶迎风离散格式进行离散，以保证计算精度.由于涉及气流分离，因此必须考虑黏性影响.合适的湍流模型是数值计算的关键，目前主要采用k-ω SST湍流模型.该模型充分发挥k-ω模型处理自由流和壁面约束流动的特点，同时借鉴JohnsonKing模型不平衡作用的思想，对于复杂流动具有普遍的适应性[10].

声场计算采用Lighthill声类比.该方法将声的产生和传播分离，也就是说，流动产生的噪声并不影响流体的内能[11].Lighthill声类比方程[12-14]在引入流场均值后可写为

注意到p0、ρ0均为常数，且密度和压力满足a20=（p/ρ）.因此，在等熵流动中湍流噪声熵源项δij[（p-p0）-a02ρa]为零.对于理想流体，涡源项ρvivj为主要声源，黏性源项τij相对较小可忽略，则Tij（x，t）≈ρvivj.由CFD非定常速度场计算结果得到时域声源项，经傅里叶变换后得到频域声源项，在频域内求解上述方程，计算该声源向远场静止无界区内的声辐射问题[15].endprint

图1为NACA0012翼型非定常绕流的计算域网格及局部放大翼型弦长c=50 mm.在亚音速条件下，计算域包括翼型前方和上、下弦长10倍区域，翼型后方12倍弦长区域.由于翼型处于运动中，为了更好地捕捉翼型表面的气动特性并适应网格运动，本文采用分区划分网格，将整个计算域划分为翼型表面的边界层（四边形网格）、边界层外的动网格（三角形网格）和动网格外的四边形网格.计算流场时采用自定义函数控制叶片及其周围的边界层网格按照一定规律运动，网格本身不变形，而边界层外的三角形网格基于弹性变形的网格调整和局部网格重构的方法实现网格的运动与更新.

2.1 俯仰运动

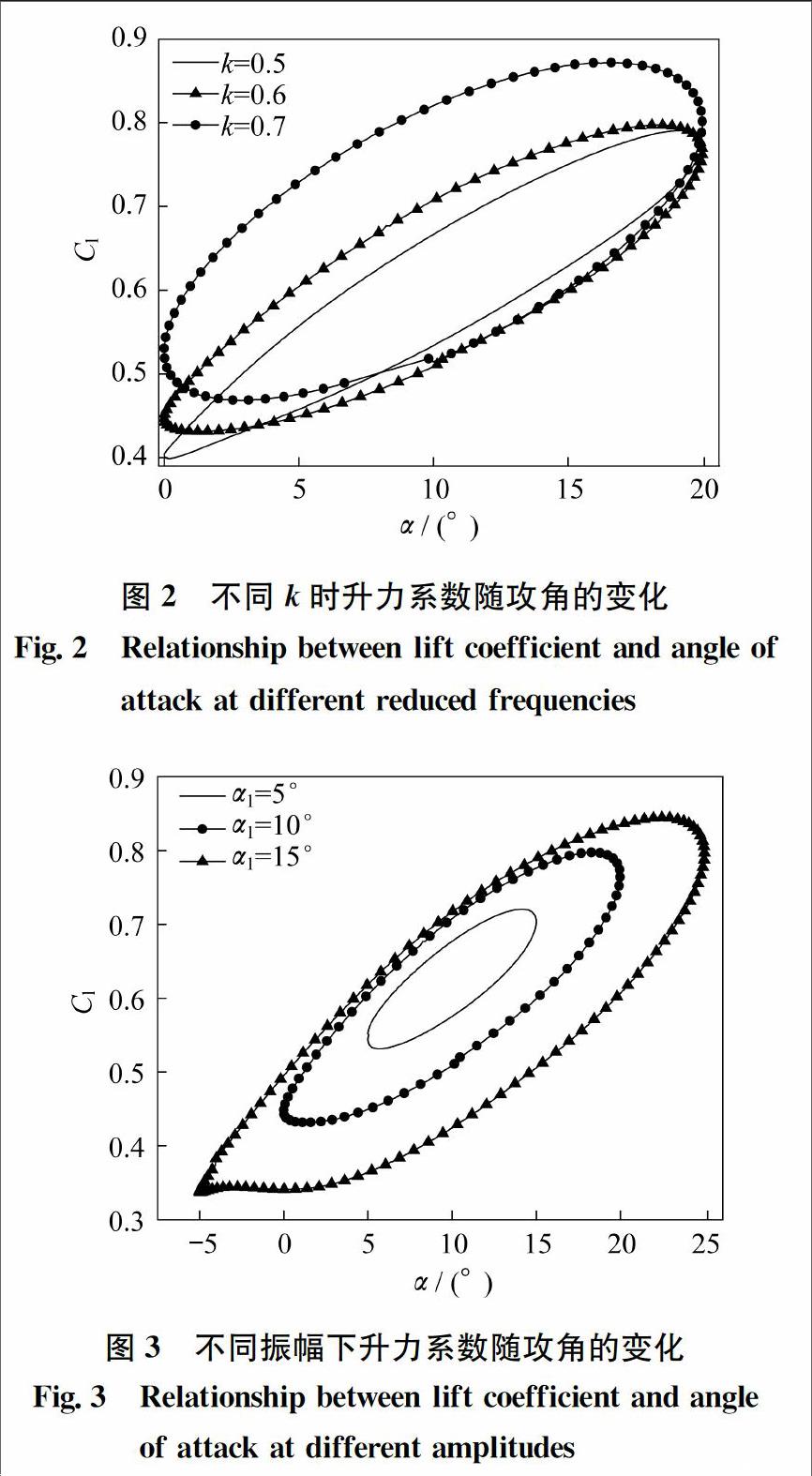
图2为相同振幅（α1=10°）下翼型做不同频率俯仰运动时的升力系数Cl.从图中可看出，随着折合频率升高，翼型表面升力系数峰值随之增加，非定常迟滞效应增强，这表现为升力系数曲线变得更加饱满.这与文献[16]中描述的振荡机翼表面升力系数随频率的变化规律一致.

图3为在相同频率和平均迎角下翼型做不同振动幅值俯仰运动时的升力系数.从图中可看出，随着振动幅值增大，迟滞环面积增加，最大升力系数相应增大，该特性符合振荡翼型表面的气动特性变化规律[17]，表明本文流动计算结果可靠.

翼型振动诱发的声源主要表现为：物体运动所致的对其边界上的流体产生压缩膨胀作用的声源（单极子声源）和物体运动所致的物体表面升力对其边界上的流体产生推力作用的声源（偶极子声源）[13].

本文在计算声场时分别提取振荡翼型表面的声源信息，并在距离翼型前缘点20c的圆周上均匀设置36个监测点.图4为k=0.6、α1=10°时，声源在各频率下的声场指向性曲线，其中：f为声源频率；SPL为声压级.由图中可以看出，低频下翼型表面声源呈单极子特性，此时声场指向性在各个方向是均匀的，这是由于低频时偶极声源的辐射能力比小脉动单极球源要差得多.随着声源频率的增大，远场指向性呈偶极子分布且声压幅值总体呈下降趋势.

2.2 沉浮运动

图5为在Φ=0、y1=5 mm时翼型做不同振动频率沉浮运动时的升力系数.由图中可看出，随着k的增大，迟滞环面积增大，迟滞效应增强.

图6为Φ=0、k=0.6时翼型做不同振动幅值沉浮运动时的升力系数.由图中可知，平动振幅越大，升力系数下降越快，迟滞效应越强.平振与纯俯仰运动相比，翼型表面升力系数的变化趋势发生改变，最大升力系数变大，且迟滞现象更明显，表现为滞后环幅宽变大.这说明k和振幅对平振翼型表面气动力的影响要大于俯仰振荡.

图7为k=0.6、y1=10°时，声源在各频率下的声场指向性曲线.从图中可看出，相同k下平振与俯仰运动对外声场声压指向性的影响相似：低频下声源呈单极子分布，随着声源频率的增大，声压指向性曲线表现为偶极子，且低频下声源平均声压级最大.不同的是，纯平振时中频声源仍具有单极子的特性，且远声场平均声压级小于高频声源.

2.3 俯仰沉浮耦合运动

在k=0.6，平均迎角和平均振幅均为0时，改变相位差Φ，通过计算得到升力系数Cl随攻角和时间的变化规律.图8为不同相位差下升力系數随时间的变化.由图可知，改变相位差Φ使升力系数的脉动幅值发生了变化，在相位差Φ≤90°时，临界攻角随相位差增大而增大，升力系数的脉动幅值随相位差增大而减小.当Φ=0°时升力系数的峰值最大；当Φ=180°时升力系数的峰值最小.这表明翼型耦合振动的相位差改变了叶型的非定常气动力响应特性.

图9为各相位差下远声场的平均声压级指向性曲线.从图中可看出：当相位差Φ=0°时，远场平均声压级明显大于其他相位差下的耦合运动；当

Φ=0°和Φ=180°时，低频声源的平均声压级最大，高频次之，中频最小；当Φ=45°时，声场平均声压级

随声源频率的增大而减小；当Φ=90°时，声场平均声压级随声源频率的增大而增大.由于Φ≤90°时，翼型表面升力系数随时间的变化规律相似，声场特性也类似，即各频率下单极子声源占主导地位.不同的是Φ=180°时，中频噪声呈现出偶极子的特性，且在130°和240°方向上平均声压级较大.

3 结 论

本文选取二维NACA0012翼型，针对低雷诺数下振荡翼型的非定常气动噪声特性，采用CFD与Lighthill声类比相结合的方法，分别对俯仰、平振以及俯仰与平振耦合运动翼型的流场及其诱导的声场特性进行了数值模拟，并对得到的结果进行分析.结果表明：

（1） 随着折合频率和振幅的增大，翼型表面升力系数的峰值增大，迟滞效应也随之增强.

（2） 相同折合频率k下，平振与俯仰运动对外声场声压指向性的影响相似：低频下声源呈单极子分布，随着声源频率的增大，声压指向性曲线逐渐表现为偶极子.

（3） 纯俯仰振荡时，随着声源频率的增大，远场指向性呈偶极子分布，且声压幅值总体呈下降趋势.纯平振时中频声源指向性仍具有单极子的特性，且远声场平均声压级要小于高频声源.

（4） 俯仰与平振耦合振动时，相位角的改变对振荡翼型气动特性的影响更显著.当Φ≤90°时，各频率下单极子声源占主导地位.不同的是Φ=180°时，中频噪声呈现出偶极子的特性，且在130°和240°方向上平均声压级较大.

参考文献：

[1] 陈旭，郝辉，田杰，等.水平轴风力机翼型动态失速特性的数值研究[J].太阳能学报，2003，24（6）：735-740.

[2] 周正，李春.风力机翼型等速上仰动态失速数值模拟[J].能源研究与信息，2013，29（4）：196-200.

[3] 杨爱玲，陈康民.NACA-65-0012振荡机翼远场气动噪声的预测研究[J].上海理工大学学报，2009，31（2）：145-149.endprint

[4] 郑世华，徐永长.有翼航天飞行器高速动态气动特性试验研究[J].流体力学实验与测量，2004，18（3）：13-18.

[5] 李其畅，伍开元，郑世华，等.高速风洞大振幅俯仰动态试验技术研究[J].流体力学实验与测量，2004，18（4）：68-71.

[6] NAKANO T，FUJISAWA N，LEE S.Measurement of tonalnoise characteristics and periodic flow structure around NACA0018 airfoil[J].Experiments in Fluids，2006，40（3）：482-490.

[7] JUNG Y W，PARK S O.Vortexshedding characteristics in the wake of an oscillating airfoil at low Reynolds number[J].Journal of Fluids and Structures，2005，20（3）：451-464.

[8] 史志偉，耿存杰，明晓，等.旋翼翼型俯仰沉浮运动非定常气动特性实验研究[J].实验流体力学，2007，21（3）：18-23.

[9] 姚迪，陈康民，戴韧，等.低雷诺数振荡翼型非定常气动性能研究[J].可再生能源，2009，27（5）：15-18.

[10] 雷延生，周正贵.风力机振荡翼型动态失速特性的CFD研究[J].太阳能学报，2010，31（3）：367-372.

[11] 王东，张学亮，李奇.Helmholtz共振腔气动噪声数值仿真[J].计算机辅助工程，2012，21（6）：5-10.

[12] GOLDSTEIN M E.Aeroacoustics[M].New York：McGrawHill，1976.

[13] 张强.气动声学基础[M].北京：国防工业出版社，2012.

[14] 李强，陈迎春，李亚林.基于混合求解法的二维多段翼气动噪声特性分析[J].民用飞机设计与研究，2013（2）：8-12.

[15] 杨晓宇，高阳，程亚军，等.高速列车气动噪声Lighthill声类比的有限元分析[J].噪声与振动控制，2001（4）：80-84，127.

[16] 陈榴，杨爱玲，戴韧.S826叶型的非定场气动力特性的数值研究[J].流体机械，2007，35（8）：14-18.

[17] 张正秋，邹正平，刘火星.振荡翼型非定常流动数值模拟研究[J].燃气涡轮试验与研究，2009，22（3）：1-8.endprint