锅炉蛇形管弯头模弯成形数值模拟研究
2018-02-26沙万华杨强陆英豪邹洋
沙万华+杨强+陆英豪+邹洋

摘 要: 蛇形管广泛应用于大型电站锅炉的省煤器、过热器、再热器等高温高压组件.对蛇形管弯头在模弯成形过程中的结构、尺寸和残余应力变化进行了数值模拟,并通过试验数据对数值模型进行了验证.研究结果表明:弯头的圆度随弯曲角度增加呈现先上升后减小的趋势,并在45°附近达到峰值;弯头壁厚的最大变化量与弯头变形率呈线性关系,塑性应变和残余应力水平均随弯头变形率的减小而呈现整体降低的趋势;此外,弯头弯制后残余应力在受滚轮挤压侧的内表面较为明显,而在弯头外表面的塑性变形更为显著.
关键词: 蛇形管; 弯头; 模弯成形; 数值模拟
中图分类号: TK 223 文献标志码: A
Abstract: Coiltube is widely used as hightemperature and highpressure components in largescale utility boilers,such as economizer,superheater and reheater,etc.In this paper,numerical simulation study on the changes of the elbow structure,size and residual stress during the die bending process was carried out.The model was validated by the experiments.The results showed that as the bending angle increased,the roundness increased firstly,then reached the peak value at 45°,and decreased at last.The maximum changes of the tube wall thickness were linearly correlated with the deformation rate of the elbow.The elastic strain and residual stress reduced as the elbow deformation rate decreased.In addition,the residual stress existed obviously at the inner surface of elbow endline,while the elastic deformation occurred significantly at the outer surface of the elbow.
Keywords: coiltube; elbow; die bending; numerical simulation
动力锅炉作为典型的高温高压设备,对弯头质量的要求尤其苛刻.随着动力锅炉容量等级不断提升、锅炉受热面结构越来越紧凑、锅炉高温部组件材料等级越来越高,锅炉受热面蛇形管结构中弯头弯曲半径R与管道外径D的比率不断降低,从而对钢管弯头的安全性要求更为严苛.
研究人员曾运用塑性变形理论[1]对钢管弯头中的应力、壁厚、弯头中性层移动、弯矩、钢管截面的收缩率等弯头参数进行了研究,得出了相关解析计算式,但未对弯管工艺方法改变对弯管过程的影响展开研究,因此该方法对模弯的实际加工制造指导性不够.
有学者采用数值模拟方法[2-6]对弯管过程进行了研究.采用实体单元对局部网格细化,将弯模、导向块视作刚性壳单元,对相同壁厚不同外径的小口径1Cr18N9Ti管材进行有限元模拟分析.由于所分析的是R/D=5,弯头、管道原材料壁厚1 mm,D在6~10 mm之间的钢管弯头,与锅炉蛇形管的弯头没有类比性,能否指导锅炉弯管还需进一步研究.
虽然目前关于弯制的数值模拟很多,但均在单个维度上进行,未将模具对弯管的影响、弯管残余应力的分析、弯管壁厚的变化等在一个模型上进行协调系统分析.为此,有必要建立一个模型,以便能多角度反映各种边界条件对弯管质量的影响[7-8].
本文使用计算机辅助(CAE)工具对钢管在弯制中和模弯成形后的一系列结构、尺寸和残余应力变化进行数值模拟,并通过试验数据对数值模型进行验证,进而获取弯头成形相关数据、弯头残余应力数据,从力学上完整分析钢管弯制过程,有利于进一步认识钢管在弯制过程中的变化,更好地控制弯头变形,改进弯管工艺.
1 试验部分
表1为试验用弯头汇总表.将Super 304H、D=48 mm的钢管按照表1下料并弯制弯头.
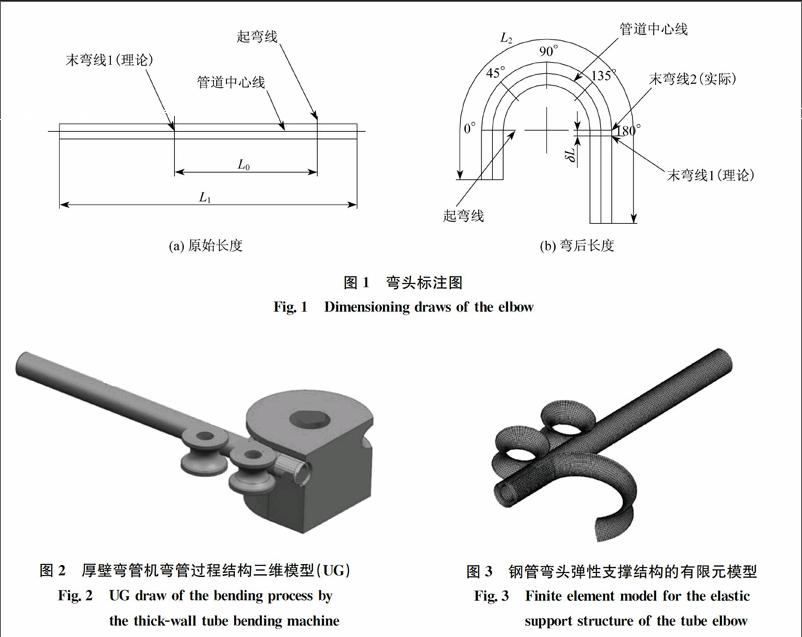
在绕弯式弯头中,弯头被夹块夹持的直段称为该弯头的前直段,弯头的另一直段相应的称为后直段.弯头角度从前直段开始计算,弯头的标注方法如图1所示,其中:L0为备料弧长(理论弧长扣除弯制中的延伸量);L1为下料总长;L2为弯后实际长度(L2=L1+δL),δL为弯制过程中的延伸量.为对试样弯头的壁厚及圆度进行准确检测,本研究对弯头进行分段切割,弯头直段从0°起每隔45°分一段,即每個弯头在0°、45°、90°、135°、180°共5个弯曲角度位置被截断,分成6段.
2 模拟部分
为了研究在厚壁弯管机上弯制的不同R/D弯头的变形及应力状况,需要对实际的弯管过程进行抽象和建模,并对计算数据与实测数据进行分析对比,检验模型的合理性,再运用模型计算结果研究弯管过程中的各种流变规律.图2为厚壁弯管机弯管过程结构三维模型(UG).
为简化模型,提高运算效率,在该模型中,不考虑弯模和滚轮自身的弹性变形,将弯模和滚轮简化为绕自身轴线旋转的刚体;将钢管简化为弹塑性体.弯模三维模型主要建立在与钢管相接触的圆弧面部分,有效降低建模工作量.endprint
为进一步提高运算效率,本研究对实体单元部分采用单点积分.
运用计算机辅助设计(CAD)建立实体模型,将其导入ANSYS软件,建立网格节点
模型,如图2所示.将建好的三维模型导入ANSYS软件进行前处理,包括面的增补、删除多余线形、更改面的法向等工作,使该模型符合CAE建模的需要.
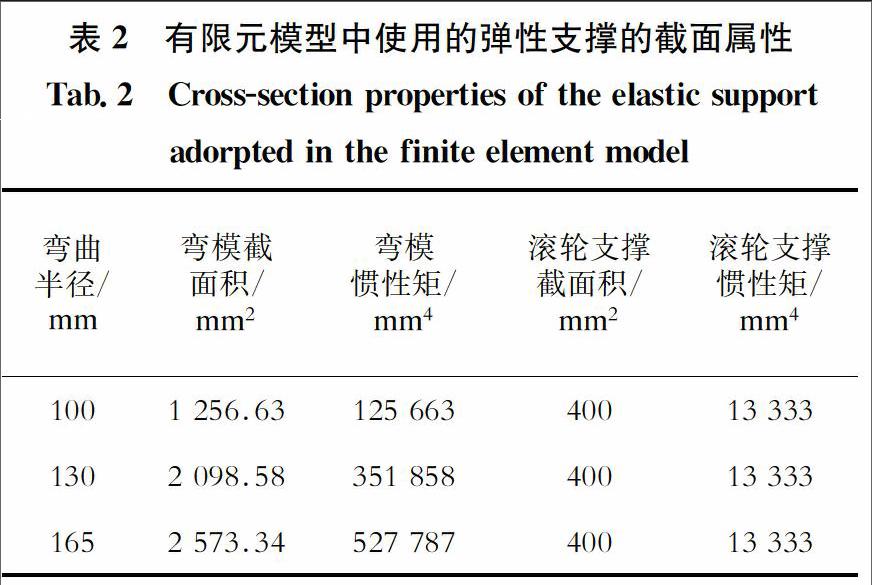
不同弯模在刚度上存在一定差别,为简化建模过程并充分反映弯模自身刚度对弯管过程的影响,将弯模简化成“梁”.在夹块夹紧力的作用下,弯模产生一定的偏转,使得钢管在变形中的边界条件随弯管过程产生一定的变化,同时也考虑滚轮架的支撑变形,使得滚轮架在弯管过程中也会发生一定的变形.各弯模的截面属性如表2所示,最终的有限元模型如图3所示.
本文将钢管设定为弹塑性体、符合双线性规则的硬化材料;接触面之间采用增强型拉格朗日准则;不考虑管模之间动摩擦与静摩擦系数差异.
模型中使用Solid 45、Beam 4和接触单元中的Target 170单元、Contact 174单元,使用Pilot Node控制弯模和滚轮的运动.在使用弹性支撑时,使用耦合函数将梁单元和Pilot Node的自由度进行耦合,对滚轮和滚轮的支撑之间的UY自由度进行耦合,对弯模和弯模的支撑之间的六个方向自由度进行耦合,固定点均建立在耦合点的另一端.表3为滚轮对钢管夹紧进给量的各载荷步边界条件.建模时,前滚轮位置标记为0 mm,加载-5 mm后与后滚轮平齐.
为研究滚轮对钢管的夹紧进给量对钢管弯头成形的影响,本文分别选取了R/D=2.08、2.71
和3.44的模型进行研究.以R/D=2.08为例,滚轮对钢管的夹紧进给量见表3.为了分析滚轮夹緊进给量的影响,还对比了夹紧进给量在标准值上下各偏离1 mm时的模拟结果.
3 结果与分析
3.1 外形及圆度
滚轮对钢管的挤压作用不仅影响钢管中应力、应变的大小及分布,同时也会对钢管的成形造成一定的影响,弯头各横截面圆度也会发生变化.例如,在钢管弯头后半段的管子内侧金属发生压缩变形,金属堆积在钢管内侧,形成“增厚”,如图4所示.模拟试验的结果与实际弯头的形状相互验证,证明了模拟的合理性.
在标准值为0 mm(定义为0方案)、标准值为+1 mm(定义为1方案)和标准值为-1 mm(定义为-1方案)三种滚轮夹紧进给量方案中,钢管的圆度变化也具有一定差异.图5为不同夹紧进给量下的圆度模拟结果.从图中可知,采用标准值(表3)的滚轮夹紧进给量能较好地预测真实弯头的圆度变化.图6为实测钢管圆度随弯曲角度变化的情况.从图中可知,实际弯头的圆度与模拟结果的趋势相同,均呈现先上升后减小的趋势,并在弯头的45°附近达到峰值,且随R/D的增大,弯头各处的圆度差异变小.
3.2 弯头壁厚变化
图7(a)、(b)分别为R/D=2.08弯头和R/D=3.44弯头各个位置处的减薄和增厚程度,弯头的减薄和增厚在钢管弯头中部变化比较平缓.由图7(a)、(b)可知,随着R/D的增大,弯头外侧减薄率和内侧增厚率呈降低趋势.在R/D=2.08 mm时,钢管外侧的壁厚减薄率为15%,内侧壁厚增厚率为10%,而在R/D=3.44弯头中,钢管外侧的减薄率降至10%,内侧壁厚增率降至7%.实测和模拟数据均显示外侧钢管壁厚的减薄量要大于内侧的增厚量.
进一步分析变形量与壁厚变化的关系,结果如图8所示.从图中可知,变形量与壁厚变化大体呈线性变化,且减薄量与增厚量相对变形量的变化并不一致,随R/D的变小(即变形量的增大),弯头内侧壁厚增厚率的增幅要明显大于弯头外侧壁厚减薄率.
3.3 应力分布
残余应力与对应位置的实际变形量并不存在数值上的一一对应关系.残余应力是应力重新分布后的结果,而塑性变形反映了弯管过程的塑性功,与变形过程中材料内部储存的能量有关.
图9、10分别为不同弯曲半径下弯头残余Mises应力及等效塑性应变的分布对比.
由图9中可见,残余应力的峰值在弯头终弯处受滚轮挤压处的钢管内表面较大,在该处的钢管外表面残余应力也较大.由图10中可知,在弯头的后半段钢管外侧受到的拉伸更加明显,塑性应变也更大.此外,塑性变形最大的位置并不是残余应力最大的位置,残余应力在受滚轮挤压的内表面较为明显,而塑性变形显著的地方始终在弯头外侧.
与R/D =2.08的结果相比,R/D =2.71的弯头残余应力的大小和分布产生了变化,残余应力大幅降低.在弯头的后半段,应力分布也发生一定的变化.在滚轮最后挤压的部位均存在应力集中的现象,但是在后半段受滚轮挤压的部分,与
R/D=2.08的结果相比,不仅应力小,而且分布
更加均匀,不存在R/D=2.08结果中的应力集中现象.这与滚轮的挤压作用减弱有关系.考虑到建模过程中增大了弹性支撑的强度,弯模在承受夹块夹紧力的情况下变形更小,滚轮在整个弯管过程中起到的作用比较稳定,没有产生条带状的应力集中带.
与R/D=2.71的结果相比,R/D=3.44弯头的残余应力有所增加,这从侧面说明残余应力分布是应力重新分布的结果.不论是R/D=2.71的弯头还是R/D=3.44的弯头,其等效塑性应变指标与R/D=2.08的弯头相比均有显著降低.
4 结 论
本文通过建立弯管过程的数值模型及试验验证,对Super 304H钢管弯头的外形、圆度、延伸率及应力分布进行了研究,得出以下结论:
(1) 本文建立的模弯成形数值模型可以较好地预测弯头的圆度及壁厚的变化趋势.
(2) 弯头的圆度随弯曲角度呈现先上升后减小的趋势,在45°附近达到峰值,且弯头变形量越小(即R/D越大),弯头各处的圆度差别越小.
(3) 弯头壁厚变化量与变形率(即R/D)呈线性关系.随着变形率增大(即R/D减小),壁厚增厚率的增幅明显大于弯头外侧壁厚减薄率.
(4) 残余应力在受滚轮挤压的内表面较为明显,而塑性变形在弯头外表面较显著.随着R/D增大,塑性应变水平和残余应力水平均呈整体下降趋势.
参考文献:
[1] 廖勇刚,余心宏,孙现龙.塑性变形理论在小半径弯管中的应用[J].锻压技术,2006,31(4):115-118.
[2] 张小昂,鄂大辛,何花卉,等.弯管壁厚变形试验及有限元模拟分析[J].现代制造工程,2008(11):56-59.
[3] 任胜乐,赖一楠,张元,等.管材弯曲成形理论与技术研究进展[J].哈尔滨理工大学学报,2011,16(6):31-35.
[4] 李君君,闻百灵,宋海波.弯管应力分析研究现状及发展趋势[J].科技风,2009(18):271.
[5] 武世勇,石伟,刘庄.缠绕式弯管工艺对管壁厚度影响的数值分析[J].锻压技术,2002,27(1):35-38.
[6] 龙会国,龙毅.奥氏体钢锅炉管冷加工固溶处理问题分析[J].华中电力,2007,20(4):72-73.
[7] 赵俐敏.几何工艺参数对热推弯管过程影响规律的研究[D].秦皇岛:燕山大学,2007.
[8] 王同海.管材塑性加工技术[M].北京:机械工业出版社,1998.endprint
