激光引信距离测量统计分布特性研究

张 伟， 李玉钊， 汪哲思， 程思敏

（北京遥感设备研究所，北京100854）

0 引言

激光引信具有指向性好、对电磁干扰不敏感、测距精度高等优势，在国内外武器领域得到了广泛使用，例如空空导弹“响尾蛇”AI M-9L导弹等［1］。随着高速模数转换器件和高速处理器的发展，在满足实时性的前提下，采用全数字方法对目标测距时，激光引信能够获得更高的测距动态特性和精度［2］。在激光回波脉冲探测模式中，由于经过目标反射的激光回波信号受目标特性、传输路径等复杂因素的影响，到达激光引信探测器的激光脉冲信号在脉宽、幅值等方面会产生变化［3］。而且激光探测器自身及光电放大电路存在随机噪声，如散粒噪声和热噪声等［4］。在全数字方法测量中，这些不确定性因素对激光引信距离测量产生影响。分析这些影响因素，有助于激光引信系统的优化设计。

本文基于脉冲激光回波的探测电路和信号处理电路模型，通过建立由电压脉冲信号和随机噪声组成的待测电压模型，在不同脉宽和信噪比条件下，利用蒙特卡罗方法研究激光引信峰值测距法的测量统计特性。

1 激光引信系统原理

激光引信一般采用脉冲激光探测体制［5］，其工作原理如图1所示。信号综合处理电路发送同步信号至半导体激光器，驱动激光器经过发射光学系统向空间内发射窄脉冲激光。如果在激光辐照范围内存在目标，则目标对激光信号形成反射。接收光学系统接收目标的反射激光并将其汇聚到激光探测器上，探测器将激光回波信号S1转换为电流信号S2，经过跨阻放大电路和主放大电路形成电压脉冲信号S3，便于后续的信号读取与测量。

后续信号综合处理电路根据电压脉冲信号和同步信号的时间差Δt来测量目标的距离r，设c为光速，则目标距离r可表示为

图1 激光引信原理示意图

如果按照同步信号的脉冲起始点为计时起始时刻点，按照激光回波脉冲的峰值点为计时终止时刻点，如图2所示。利用测量的系统延时Δt计算目标距离的方法即峰值测距法［6］。本文的研究工作将基于峰值测距法展开。

图2 激光引信峰值测距法示意图

2 信号模型

经过放大，形成的电压脉冲信号S3是激光回波脉冲信号S1的放大信号，并在时域具有相同的波形分布特征。电路中存在随机噪声，主要是由激光探测器噪声N1和放大电路噪声N2。激光引信探测的信号通道如图3所示。

图3 激光引信探测信号通道示意图

信号综合处理电路接收到的信号为待测电压S4，其中包含电压脉冲信号和噪声，表达式为

式中：u（t）为待测电压；us（t）为激光回波信号对应的无噪声信号；un（t）为光电探测信号通道中等效噪声电压。

经过目标反射的激光回波信号比较复杂，一般体现在幅值、脉宽等方面的变化。根据实测数据，可以近似地认为电压脉冲信号S3在时域上是服从重尾函数分布形式［7］，其特点是上升沿陡、下降沿缓，电压脉冲信号可表示为

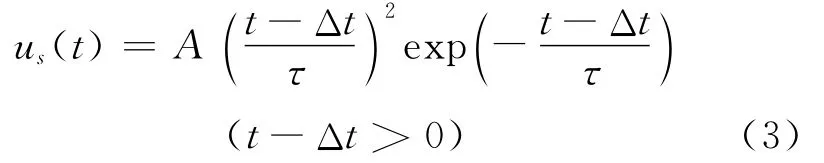
式中：A为与脉冲峰值有关的参数；τ为脉宽；Δt为探测系统时延。当t-Δt=2τ时，重尾函数取峰值，以us-p表示电压脉冲信号的峰值，则有

随机等效噪声电压信号的概率密度函数可用的高斯函数表示为［8］

式中：σn为等效噪声电压概率密度标准差；un为等效噪声电压值。则待测电压的信噪比为us-p/σn。

3 激光引信的峰值测距仿真与分析

对于确定的电压信号和随机噪声分布，利用蒙特卡罗仿真方法可以研究电压脉冲信号的脉宽、待测信号信噪比等因素对激光引信峰值测距的影响［9］。设激光引信仿真初始设置参数：τ=10 ns，Δt=40 ns，r=6 m，us-p=200 mV，σn=10 mV，SNR=50。仿真某次待测电压的波形图如图4所示。可见，待测电压的峰值已不明显，如果取最大值为峰值时，可能已经偏离电压脉冲信号的峰值，对应的计时终止时刻也会发生偏移，造成激光引信的距离测量误差。

图4 待测电压示意图

蒙特拉罗仿真次数为10 000次，单次仿真的时间分辨率为0.5 ns，对应的目标距离分辨率为0.075 m。相应的计时起始时刻点均为0，计时终止时刻点为待测电压的最大值点。在同一条件下，经过蒙特卡罗仿真，将10 000次的计时终止时刻点作为统计样本，画出直方图，得到激光引信峰值测距法的测量统计特性。其中，单位统计区间为0.5 ns。最后对直方图进行高斯拟合，使结果表示清晰。

3.1 不同电压脉冲信号脉宽

设置初始参数：Δt=40 ns，r=6 m，us-p=200 mV，σn=10 mV。脉宽分别设置为4，6，8，10，12，14 ns。针对不同脉宽，经过蒙特卡罗仿真，得到对计时终止时刻点的统计直方图的高斯拟合如图5所示，统计均值和方差如表1所示。

图5 不同脉冲宽度的测量统计直方图拟合

表1 不同脉宽条件的测量统计均值和标准差

由图5和表1可以得出两个结论。一、如式（3）所示，仿真的计时起始时刻设置为同步信号的上升沿，所以在脉宽不同的情况下，发射脉冲信号和回波脉冲信号的峰值位置也不同。脉宽越窄，峰值时刻位置越提前，这部分测量误差属于系统误差，在特定系统中，通过补偿可以消除。当脉宽相差2 ns时，计时终止时刻理论上应相差4 ns，与表1中相邻统计均值之差基本吻合。当脉宽越大时，统计均值仍然呈现出稍微增大的趋势，但不明显，可以忽略不计。二、脉宽越大，计时终止时刻的统计标准差越大，统计分布越分散，表明测距精度下降。当脉宽为4 ns时，测距数据的统计标准差为0.143 m，而当脉宽为14 ns时，测距数据的统计标准差为0.443 m，变化较明显。因此，在激光引信系统设计时，减小发射信号的脉宽有利于提高系统的测距精度。

3.2 不同的待测电压信号的信噪比

电压信号的脉冲峰值和随机噪声共同决定待测电压的信噪比。仿真初始设置参数：τ=10 ns，Δt=40 ns，r=6 m，us-p=200 mV。仿真过程中改变等效噪声电压概率密度标准差来改变信噪比。等效噪声电压概率密度标准差分别设置为4，8，12，16，20 mV，相应的信噪比分别为50.0，25.0，16.7，12.5，10.0。针对不同信噪比，蒙特卡罗仿真得到对计时终止时刻点的统计直方图的高斯拟合如图6所示，统计均值和方差如表2所示。当电压信号脉宽τ=10 ns时，理论上计时终止时刻的补偿值为-20 ns。

图6 不同信噪比条件的测量统计直方图拟合

表2 不同信噪比条件的测量统计均值和标准差

由图6和表2也可以得出两个结论。一、随着系统信噪比的下降，计时终止时刻点的统计均值逐渐远离补偿前的值，但变化不大。信噪比从50降至10时，统计均值的变化量为0.41 ns，对应的测距变化量为0.06 m，可以忽略不计。二、随着系统信噪比的提高，计时终止时刻点的统计标准差逐渐减小，统计分布越集中，测距精度越高。信噪比为10时，测距值的统计标准差的为0.46 m，而当信噪比为50时，测距值的统计标准差的为0.21 m。提高激光引信探测系统的信噪比，有利于提高测距精度。

4 结论

通过建立激光回波脉冲探测模型，利用蒙特卡洛方法，仿真激光引信峰值测距法测量的统计分布特性。结果表明，脉冲宽度和信噪比能显著影响测量的统计分布，当仿真初始设置参数为τ=10 ns，Δt=40 ns，r=6 m，u s-p=200 mV 时，脉宽越小，信噪比越大，测量的统计分布越集中。减小激光引信发射信号脉宽，提高探测系统信噪比，有利于改善激光引信的测距精度。