基于ARM的小型化SINS/GNSS组合导航系统设计*
2018-02-21李小博卢宝锋王新龙陈文海
陈 沣,李小博,卢宝锋,王新龙,陈文海
(西安现代控制技术研究所,西安 710065)
0 引言
随着现代无人机小型化、轻量化,对于导航系统的体积、重量要求越来越严格。目前应用于无人机组合导航系统主要是由捷联惯性导航系统(SINS)、卫星导航系统(GNSS)等进行组合导航。由于SINS误差随时间发散,长时间导航系统需要于GNSS进行组合。
ARM是有英国ARM公司设计的一系列32位RISC微处理器的总称,在数据处理能力上已经可以满足组合导航的运算速度要求,在成本上相对DSP有显著的优势。
在惯性导航系统的选择方面,为了在性能不受影响的情况下达到体积最小、重量最轻,选用分立的MEMS陀螺/加速度计成为了最优方案。
1 SINS/GNSS系统软硬件设计
组合导航系统的硬件部分由惯性测量组件、卫星定位仪、计算采集部分等组成。其中MEMS陀螺选用3个AD公司的单轴陀螺ADXRS642,零位稳定性约为180°/h;MEMS加速度计选用两个AD公司的双轴AD22293,零位重复性误差约为5 mg。陀螺以及加速度计的空间布置方式保证载体系前上右3个方向均至少与一个器件的敏感轴重合。MEMS陀螺、加速度计输出的模拟量由AD7689进行采样,通过SPI总线与处理器芯片通信。处理器芯片选用意法半导体的STM32F401RE,最高主频84 MHz,具有浮点运算单元(FPU)。GNSS芯片选用瑞士ublox公司的NEO-M8N芯片,输出频率最高10 Hz,通过TTL电平与处理器芯片的USART接口通信。整个系统实现体积小于90 mm×50 mm×10 mm,重量小于120 g。
组合导航系统的软件部分由驱动软件、ARM架构软件及算法软件组成。处理器间隔0.5 ms对AD7689采样的结果进行一次采集,间隔10 ms进行一次惯性导航解算与卡尔曼滤波时间更新;收到GNSS发出的速度、位置信息,在下一个10 ms解算周期加入卡尔曼滤波量测更新,对姿态角、位置、速度进行反馈矫正。
2 惯性导航算法
由于MEMS器件采用印制电路板焊接方式保持的垂直度,MEMS陀螺和加速度计对应3个敏感轴的安装误差较大,需要用标定方法进行补偿。在不同温度下MEMS陀螺和加速度计的刻度系数与零位也不同,在这里近似认为是线性变化。
令载体坐标系为b(前上右),导航坐标系为n(北天东),惯性坐标系为i。载体系下比力为:
fb=KaUaccg
(1)
式中:Ka为相应温度区间的加速度计刻度系数3×3矩阵,经过预先标定得到[1];g为重力加速度;Uacc为AD测得的3个加速度计电压扣除相应温度区间零位的值。
载体系下角速率为:
(2)
式中:Kω为相应温度区间的陀螺刻度系数3×3矩阵,经过预先标定得到[2];Ugy为AD测得的3个陀螺电压扣除相应温度区间零位的值。
载体系下比力fb转到导航系下为fn,扣除重力加速度g值可以得到导航系、载体系下加速度an、ab。
则导航系下速度迭代可以表示为:
Vn(t)=Vn(t-dt)+dt·an
(3)
式中:dt为惯性导航解算周期。
大地系下纬度、经度、高度迭代如下:
(4)
式中:Rm为子午圈曲率半径;Rn为卯酉圈曲率半径;Vn、Vu、Ve分别为北天东速度。
导航系相对惯性系的旋转角速率为:
(5)
式中:ωie地球自转角速率。
载体系相对导航系旋转角速率在载体系下投影为:
(6)
令
(7)
(8)
姿态四元数迭代可以表示为[4]:
(9)
将上式泰勒展开即可以得到相应阶数的姿态四元数离散迭代方式。通过姿态四元数又可以得到相应时刻的姿态转换矩阵进而得到姿态角[3-4]。
3 组合导航方案设计
卫星导航芯片间隔约100 ms输出载体位置、速度。令卫星导航芯片输出的位置、速度分别为Psat、Vsat。
线性条件下,系统的状态方程和量测方程的简化形式为[7]:
(10)
Zk=HkXk+Vk
(11)
式中:Xk为k时刻系统状态;Zk为k时刻测量值;Φk/k-1为tk-1时刻至tk时刻的一步转移阵;Γk-1为系统噪声驱动阵;Hk为量测阵;Vk为量测噪声序列;Wk-1为系统噪声序列
(12)

时间更新迭代方程为:
状态一步预测[5]:
(13)
一步预测均方误差:
(14)
式中,Q为系统噪声协方差阵[6]。
量测更新迭代方程为:
(15)
式中:ZK为k时刻量测值,LSINS、VSINS分别为惯性导航解算得到的位置、速度,LSAT、VSAT分别为卫星导航芯片输出的位置、速度。
滤波增益[5]:
(16)
状态估计[5]:
(17)
均方误差[5]:
(18)
式中R为量测噪声协方差阵[6]。
由于在缺乏水平机动的情况下,航向角观测性较差[7],故组合导航在平直运动时利用卫星导航相对地面的速度航向纠正航向角。算法采用序贯卡尔曼滤波方式设计。
令航迹角Yyaw与航向角ψyaw误差为Δψ
Δψ=Yyaw-ψyaw
(19)
Yyaw由GNSS水平速度得到,ψyaw由惯性导航解算得到,Δψ定义域取为[-π,π)。
引入航向量测量[8]:
Zyawk=Δψk
(20)
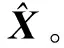
4 组合导航系统车载实验分析
为了验证组合导航总体性能,2017年10月进行了跑车实验。跑车路线为近似直线路线、中途无停顿。共有两组有效数据进行评估。车载高精度惯性导航系统的姿态角误差小于0.02°/h。车载GPS位置精度优于10 m、速度精度优于0.5 m/s。将车载导航系统的输出与文中所述导航系统输出进行比较,误差统计表格如表1所示。
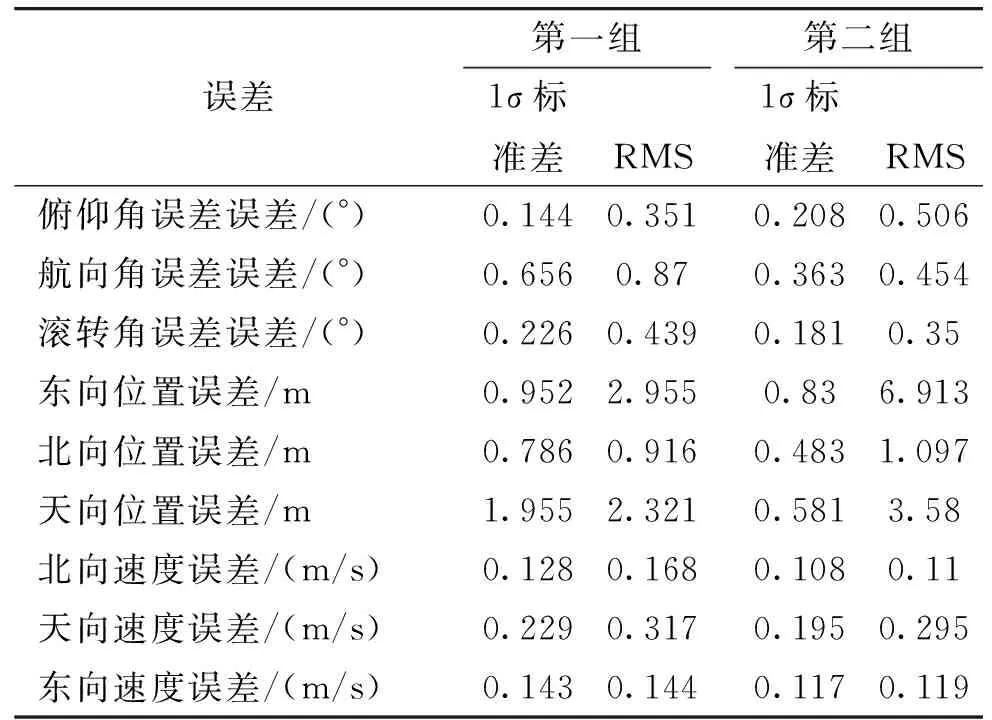
表1 误差统计表格
姿态角误差统计结果包括了初始安装误差、初始对准误差。取两组中较差的RMS统计值,滚转角、俯仰角误差约为0.5°,航向角误差约为0.9°。
得到的误差曲线如下:
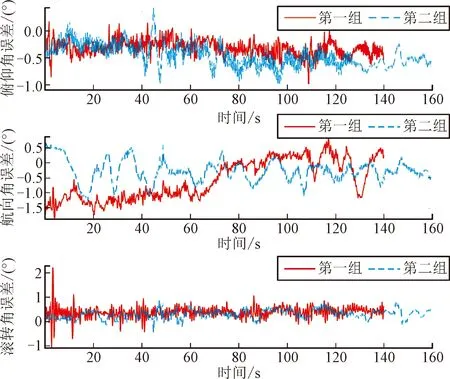
图1 姿态误差曲线
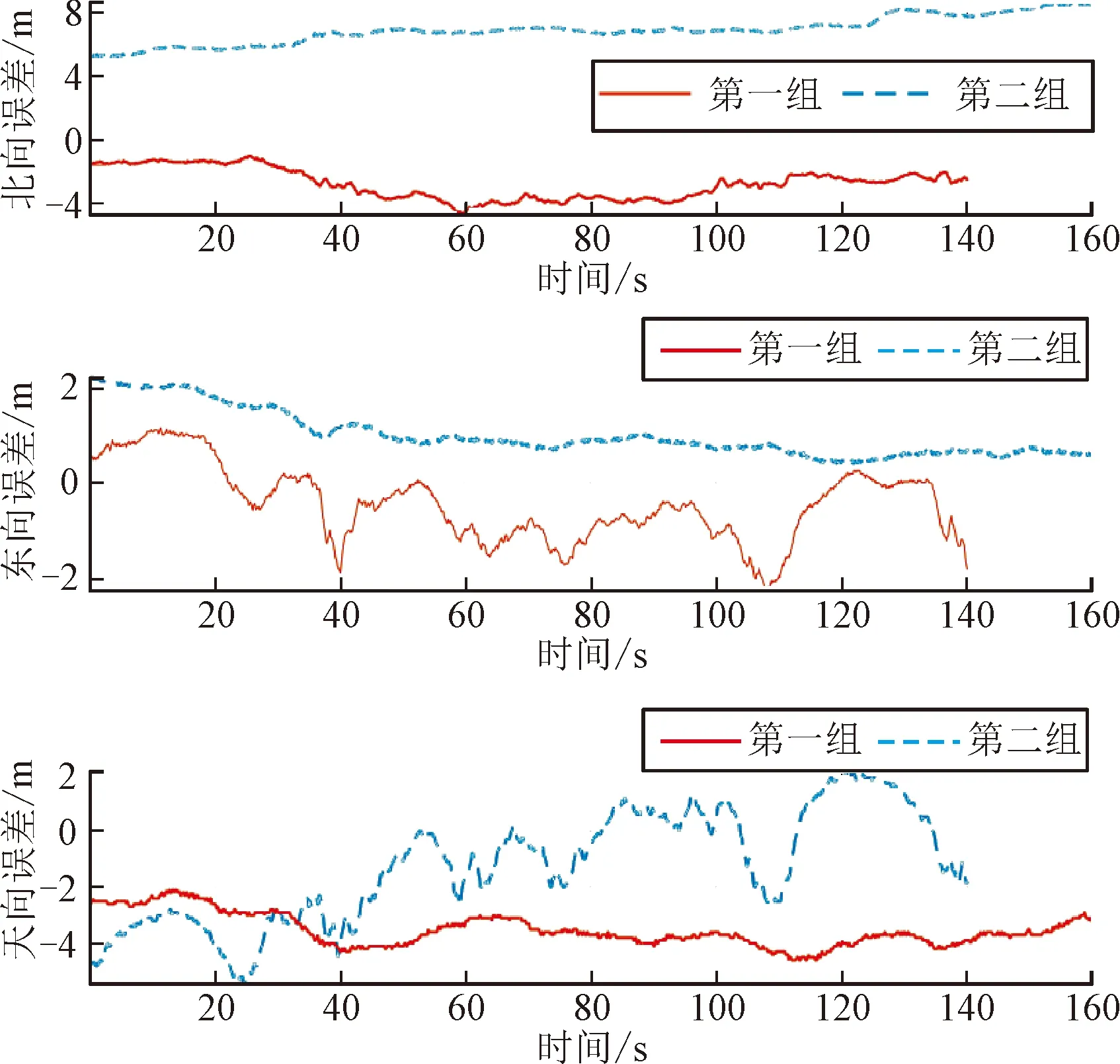
图2 位置误差曲线
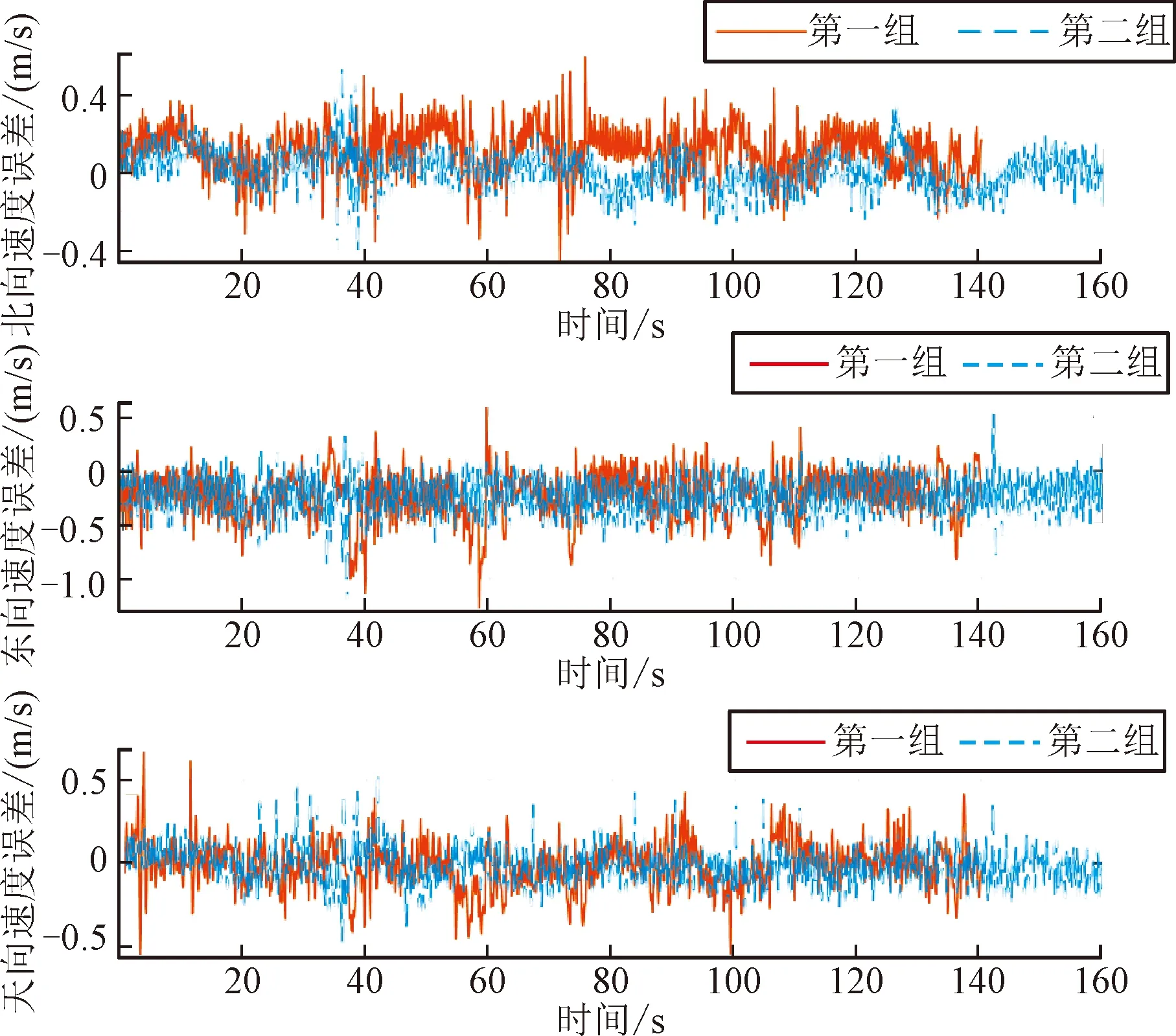
图3 速度误差曲线
由位置、速度统计数据及曲线可以看出,组合导航系统位置、速度精度应优于或等于车载GPS精度。
由于所用陀螺零位漂移达到0.05°/s,160 s漂移约为8°。从姿态角误差曲线来看,误差基本保持在1°以内,误差保持收敛状态。航向误差由于其观测性差,当载体近似匀速直线运动时仍然会发散。加入航向量测后,航向角误差成功收敛到1°以内。
5 结论
利用低成本、小型化MEMS IMU器件进行惯导解算,与微小型GNSS芯片低频率输出的位置、速度信息进行卡尔曼滤波松组合,可使姿态角、位置、速度误差保持在较小范围内。实验结果表明,在微小型无人机等对空间、重量要求严格的应用中,该设计具有显著意义。
