新课程理念下优化数学课堂教学的探索

2018-02-18王信金

中学课程辅导·教师教育（中） 2018年12期

王信金

【摘要】新课程理念强调学生是学习的主体，学习活动是学生在已有的知识和经验的基础上主动构建的过程，教师的角色也要由以往单一的讲授者转变为的组织者、引导者、合作者。只有转变教师教育观念，提高课堂教学质量和效率，才能真正实现由应试教育向素质教育的转变。

【关键词】新课程理念数学课堂教学

【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711（2018）12-019-02

一、激发学科情感，形成内在动力

数学学科的历史发展和许多科学家的体验表明：数学学习不仅包括对知识的掌握，而且更离不开丰富的情感基础。

笔者在教学中出示过这样一道题：如果正n边形的一个内角等于外角的3倍，那么这是正边形。

实践表明，只要教师能转变观念，就能从教材中挖掘出蕴含着的丰富的情感来，调动学生参与数学教学的积极性，就会形成内在的学习动力。

二、突出数学应用，培养应用意识

数学知识来源于自然界和人们的实际需要。事实上，数学科学的许多重要理论，都是因应用而产生、为应用而发展起来的。而学生所学的数学知识呈现的只是整理加工过的严密、抽象、精炼的数学结论，与现实生活脱节。我们教学工作的一项重要任务，就是让学生亲自参与“知识再发现”的过程，经历探索过程的磨砺，为数学应用做好必要的准备。

例如有一道几何作图题：已知△ABC，作出这个三角形的内切圆。

笔者将其改为：现有一块三角形的铁板，要将它裁成面积最大的一个圆，应怎样设计。

两道题叙述不同，但内涵相同。

显然改动前的那一道题被“纯数学化”了，这类题目给人一种错觉：数学就是数学，现实就是现实，数学中没有现实。而改动后的题目给出一种现实环境，以解决现实困难为目的。这无疑对激发学生学习兴趣，培养学生应用数学的意识很有好处。

从发展应用能力、培养学生的创造精神这个角度，教师应注意设计一些非常规、与教材有较多联系、学生能够理解和喜欢的“数学问题”。

三、引导自主探索，提高操作能力

在数学教学中要依据学生的年龄特点和认知水平，设计探索性和开放性的问题，给学生提供自主探索的机会，使学生理解数学问题是怎样提出的，数学的知识是怎样形成的，数学理论是怎样发展的，从中领悟到数学中的辨证关系。如：教学“三角形内角和定理”，先由学生作图，并测量三个角大小，并做出猜想;然后，让学生动手把三角形的三个角剪下来拼在一起，发现三个角组成一个平角，再次验证猜想得到的结论：“三角形三个内角的和等于180°”。同时，使学生认识到：尽管全班45位同学画了45个各不相同的三角形，测量结果和拼接结果都得出了“三角形三个内角和等于180°”的结论，但客观實际的三角形有无限多，画不完亦量不完，45个存在的关系绝不能断定就是所有三角形内角和的结论，更何况这些测量的过程存在误差，只有经过逻辑证明才能认定。最后引导学生：由于拼接的过程实际就是角的移动过程，因而联想到作平行线的方法分割平角，从而完成本题的证明。

四、启发创造诱因，培养创新思维

在日常教学中，根据学生的特点和认知水平，经常性地选择一些发散性强的数学知识或问题，采取适当的启发，让学生主动地去探索数学真理，形成创造气氛。

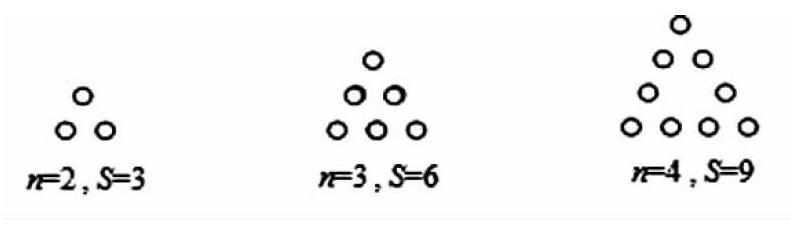
例如：下列各个图是由若干盆花组成的形如三角形的图案，每条边（包括两个顶点）有n（n>1）盆花，每个图案花盆的总数是S。按此规律推断，S与n的关系式是。

本题是一道用归纳、递推的思想求数列通项的开放性试题。但初中生未系统学习过有关数列的知识，怎样才能启发学生的创造思维，培养学生创新的能力呢？笔者编拟了3道“爬坡式”题组，用探索、联想、拓广的方法，激发学生的创造力。

（1）探索邻近的两个图形或数据有什么样的关系？

（2）想象它具有什么性质，推断s与n（当n分别为2、3、4）时的关系表达式。

（3）根据这些推测和猜想再设计：当n=5时，请画出图形并求s的值。验证当n=5时，s=3（5-1）的正确性;进而推广到当每条边有n盆花时s=3（n-1）这一普遍性的规律。

从而发现和解决该种类型题的一些新思想和新方法。这一过程看来虽很简单，但其中已经闪现了丰富的想象活动并蕴含着创新的因素。当然，在启发时应注意要把握好“度”，预防启而不及或太过。

五、寻找思维途径，拓宽解题思路

爱因斯坦曾经说过：“提出一个问题往往比解决一个问题更重要，而提出新的问题，却需要有创造性的想象力。”。教师在课堂上不仅重视如何解决具体的数学问题，要更加重视教会学生如何发现问题和提出问题。而引导学生多进行一题多解，一题多变，一法多用的训练，是拓宽学生的解题思路，培养学生解决问题的最优意识的方法之一。

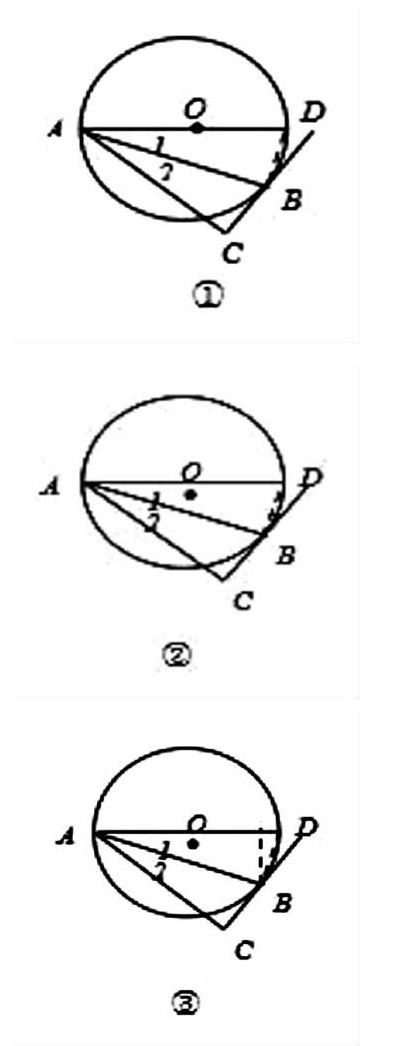
例如：如图，已知AD是直径，AB是弦，BC是切线，AC垂直于BC，求证：∠1=∠2.

这是一道一题多解的训练题，一些教师出示题目后，就开始讲解本题的多种解法，这样的结果就会造成许多学生不明白为什么会有怎么多解题方法。其症结所在就是：教师只注重问题的解决，而在教学中未能充分暴露其寻找解题途径的过程。

前面讲到的：提出一个问题往往比解决一个问题更重要。这句话里其实包含这样的一个意思——如何根据题目的特征，提出可能的解题方案。

教学中可根据题目特征，引导学生从不同的角度去分析思考，得到一题多解的思路。

思路一：由于∠1、∠2是圆周角，BC是切线，当然有弦切角。问题提出——能否利用弦切角与圆周角的关系，利用第三个量过渡，证明两角相等？

解决问题：连结BD得∠1=∠3，再利用∠1、∠3和∠4、∠2互余得∠3=∠2，则∠1=∠2

思路二：由于∠1、∠2是分别是△ABD与△ABC的内角。问题提出——能否利用利用三角形相似的性质，证明两角相等？

解决问题：连结BD，∠ABC=∠D，∠C=∠ABD，则△ABD∽△ABC，得∠1=∠2.

思路三：在几何证明中常利用三角形全等的性质证明两个角相等，而本题中△ABC为直角三角形，问题提出——能否构造两个全等的直角三角形，证明两角相等？

解决问题：作BE⊥AD，连结BD，证明△ABE≌△ABC，得∠1=∠2.

从本题的分析过程来看，教师能够引导学生从各个角度、各个方面、各种联系去认识问题，激活学生的思维，增强他们的问题意识，从而达到拓宽学生解题思路的目的。

数学的许多发现都是在不断地尝试、失败、总结、提升中实现的。要允许学生按自己的经验对题目的理解，以及所选择的方法和途径进行解题。如果“失败”了，教师应及时指出失败的原因。只有在不断的错误与失败中总结经验，提高认识，最终才能尝到成功的乐趣。