基于蚁群算法的黄河金三角旅游路线规划研究

杨晓敏

摘  要： 选择一条合适的旅游路线对于旅游者非常重要。蚁群算法运用到黄河金三角旅游路线的规划中，选取黄河金三角的11个景点，把选取的景点转换为经纬度，然后用蚁群算法进行路径优化。通过对蚁群算法的参数的调整和算法的改进，用Matlab进行仿真实验，并进行了仿真分析，结果表明，蚁群算法能很快收敛并得到最优路径。

关键词： 旅游路线; 路径优化; 蚁群算法; Matlab

中图分类号：TP391.9          文献标志码：A     文章编号：1006-8228（2018）12-61-03

Abstract： Choosing a suitable tourist route is very important for tourists. In this paper， ant colony algorithm is applied to the planning of the Yellow River Golden Triangle tourist route， 11 scenic spots in the Yellow River Golden Triangle are selected， and the selected scenic spots are converted into latitude and longitude， then the ant colony algorithm is used for path optimization. Through the adjustment of the parameters of ant colony algorithm and the improvement of the algorithm， simulation experiment is carried out with MATLAB， and the simulation analysis is carried out. The results show that the ant colony algorithm can converge quickly and get the optimal route.

Key words： tourist route; path optimization; ant colony algorithm; MATLAB

0 引言

我国国民经济迅速发展，人们生活水平普遍提高，休闲方式发生了巨大改变，我国的旅游业处于蓬勃发展的阶段。由于我国小长假增多，所以短期旅游线路受到广大人民群众的欢迎，如何规划一条最佳旅游路线，是行业内的研究热点。

旅游路线的规划本质是组合优化问题，也是一个NP难题，组合优化问题很难求出最优解，所以我们试图找到一种近似最优解，经过研究发现蚁群算法具有这种特性，所以把蚁群算法应用到旅游路线的规划中，帮助我们找到近似最优解[1-2]。

1 蚁群算法的优点

蚁群算法是20世纪90年代初由意大利学者M.Dorig等人提出的一种模拟进化算法，蚁群算法是一种生物仿生算法，仿照蚂蚁的走路行为，建立相应的数学模型，从而把相应的算法与实际应用结合，使实际问题得到解决。算法的基本思想是蚂蚁在觅食的过程中会留下信息素，那么在设计算法的时候给了一个信息素参数，根据信息素的浓度来判断选择某条路径的概率。蚁群算法有它本身的缺点，比如收敛速度慢、容易停滞，为了解决蚁群算法的缺陷，很多学者都提出了相应的改进算法，德国学者Thomastuzle和Holerhoos提出的最大最小系統，在解决TSP问题时效果要优于一般的算法，还有一些学者把蚁群算法和一些其他的仿生算法相结合，比如意大利学者Fabio Abbattista等人提出了遗传算法和蚁群算法相结合的组合优化算法[3]。蚁群算法的优点如下：

⑴ 算法模拟蚂蚁的行为，是一种无控制中心，并且为分布式的控制方式。

⑵ 算法的机制属于正反馈机制。

⑶ 算法的稳定性较好，可以应用于众多的实际问题。

⑷ 是一种多主体协作的智能算法。

⑸ 易与其他算法融合，解决相应的实际问题。

2 蚁群算法的数学模型

蚁群算法主要通过蚂蚁留下的信息素的数量来判断该段路段的重要程度，残留的信息素与蚂蚁选择该路断的可能性呈线性相关，留下的信息素越多，选择的可能性就赵大[4-5]。

蚁群算法的数学模型，关键是状态转移概率，用pijk来给示蚂蚁k从城市i转移到城市j的状态转移概率，j是尚未访问的城市，则状态转移概率pijk如式⑴所示。

式中，allowedk={0，1，…，n-1}表示蚂蚁k下一步允许选择的城市。α表征信息素重要程度的参数，β表征启发式因子重要程度的参数[6]。为每只蚂蚁设置一个禁忌表，主要用来记录蚂蚁走过的城市，不允许在本次循环中重复经过，循环结束后禁忌表清空，下次重新记录。

每完成一次循环，对信息素进行更新，如式⑵和式⑶所示。

3 蚁群算法在旅游路线规划中的应用

蚁群算法用于解决NP难题，与旅游路线的规划相契合，因此把蚁群算法应用到旅游路线的规划中。本次仿真实验选取黄河金三角的11个景点，分别位于山西省、陕西省、河南省。通过百度地图得到了11个景点的经纬度，11个景点的经纬度如表1所示。

算法的基本步骤如下：

⑴ 初始化算法的相关变量。

⑵ 将m只蚂蚁放到n个城市上。

⑶ 蚂蚁按照式⑴的概率函数选择下一城市。

⑷ 记录本次迭代的最佳路线。

⑸ 更新信息素。

⑹ 把禁忌表清零。

3.1 参数的设置与仿真结果的关系

⑴ 蚂蚁数量m值对仿真结果的影响

研究m值不同， Alpha=0.5、Beta=1、Rho=0.1、NC_max=200、Q=100迭代次数的变化情况。

当m=31时，得到的路径为8—5—6—4—1—9—10—11—2—3—7，在第2次迭代时收敛，最短距离为288.4376。

当m=21时，得到的路径为5—6—4—1—9—10—11—2—3—7—8，在第5次迭代时收敛，最短距离为288.4376。

当m=11时，得到的路径为5—6—4—1—9—10—11—2—3—7—8，在第六次迭代时收敛，最短距离为288.4376。

从以上仿真结果可以看出，蚂蚁数量影响算法的收敛速度，但是如果蚂蚁数量远远大于31时，效果将不明显，所以选择合适的蚂蚁数量是非常必要的。同时还可以发现由于实际中晋城所处的地理位置，所以在遍历时有时做为起点，有时做为终点。

⑵ 研究Beta值对仿真结果的影响

研究当Beta值不同，m=31、Alpha=0.5、Rho=0.1、NC_max=200、Q=100迭代次数的变化情况。

当Beta=1，在第4代的时候收敛。

当Beta=5，在第7代的时候收敛。

当Beta=10，在第3代的时候收敛。

实验结果表明，Beta值和收敛次数之间没有线性关系，要根据经验值取得最佳值。

3.2 仿真

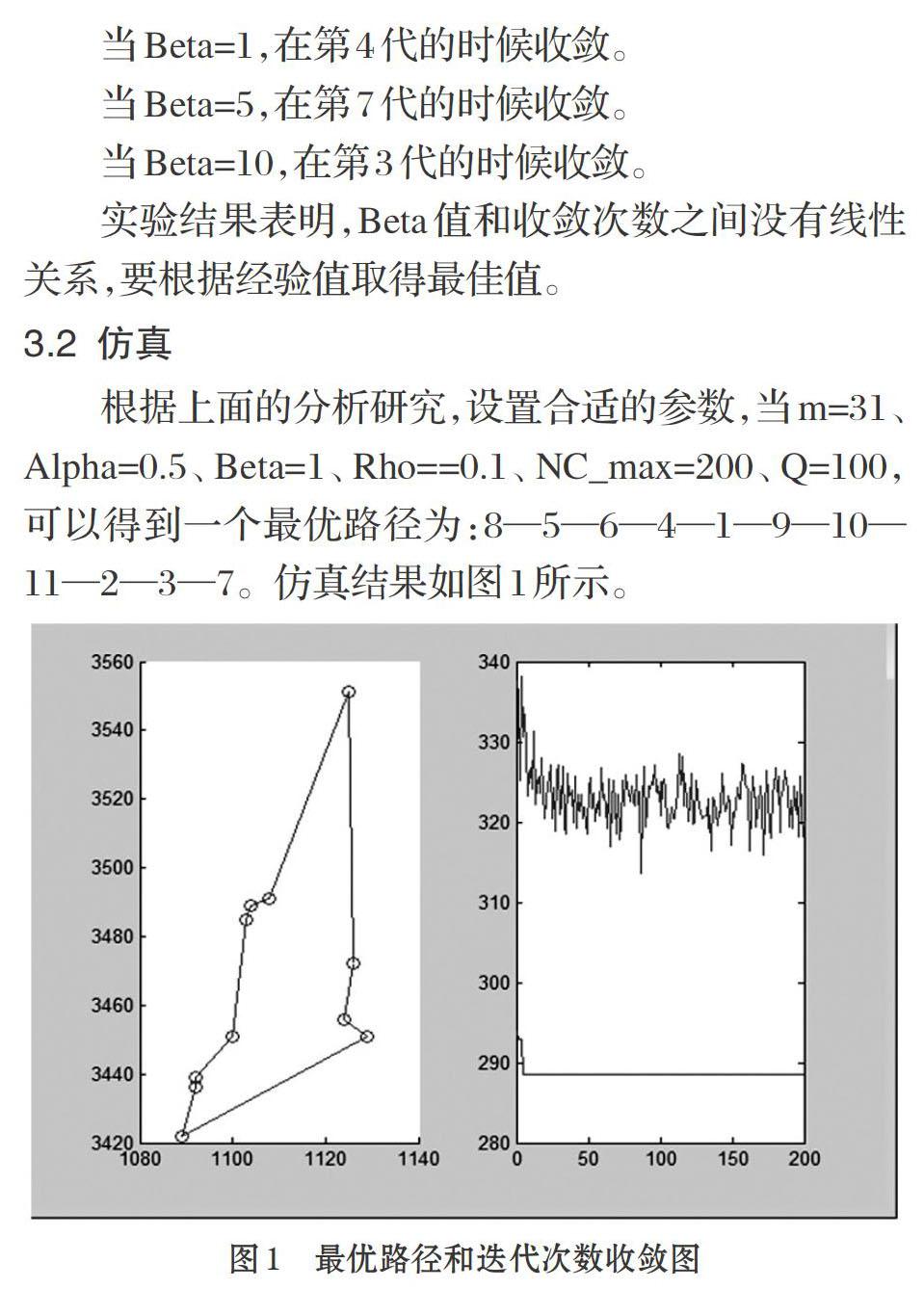
根据上面的分析研究，设置合适的参数，当m=31、Alpha=0.5、Beta=1、Rho==0.1、NC_max=200、Q=100，可以得到一个最优路径为：8—5—6—4—1—9—10—11—2—3—7。仿真结果如图1所示。

3.3 仿真分析

通过仿真实验可以看出，算法在第5次迭代的时侯就已经收敛，得到的路径为8—5—6—4—1—9—10—11—2—3—7，最短路径为288.4376，通过分析可知，路径基本按照省份呈三个集群，分别是景点8、5、6、4属于山西省，景点1、9、10、11属于陕西省，景点3，2、7属于河南省，基本符合实际。

4 结论

本文研究了蚁群算法在旅游路线规划中的应用，并研究了算法参数对仿真结果的影响，发现蚂蚁个数对收敛速度的影响较大，在一定范围内呈线性增长，而Beta值对算法的收敛没有呈现线性的关系，需要根据经驗得到合适的参数。通过仿真实验表明，算法具有较好的收敛性，能快速找到最优路径。不足之处是没有考虑实际道路对整个路线规划的影响，后续研究应该把实际道路抽象成权值和费用两个参数加入到算法的仿真中，可以得到更符合实际的结果。

参考文献（References）：

[1] 李进立，韦程东，刘广会，王一茸.旅游路线规划问题[J].广西示范学院学报，2016.3：30-37

[2] 吴小芳，龚丹丹.大岭山森林公园特色旅游路线设计及系统开发[J].福建林业科技，2015（2）：174-178

[3] 金飞虎，洪炳熔，高庆吉.基于蚁群算法的自由飞行空间机器人路径规划[J].机器人，2002.24（6）：526-529

[4] 魏平，熊伟清.用于一般函数优化的蚁群算法[J].宁波大学学报（理工版），2001.14（4）：52-55

[5] 闫登福.基于距离可达矩阵的自驾游路线优化研究[D].东北大学，2012.

[6] Dennis Huisman， Albert P. M. Wagelmans. A solution approach for dynamic vehicle and crew scheduling[J]. European Journal of Operational Research Volume： 172， Issue： 2， July 16，2006：453-471