初中数学教学中创新思维的培养探究

广州市番禺区石碁第四中学 冯锦洪

一、夯实“四基”，培养创新思维

创新思维的培养充分体现在数学的“四基”教学中。“四基”即基本数学知识、基本数学技能、基本数学思想方法、基本数学活动经验。“四基”教学和创新思维是互相联系的，谁也离不开谁，否则就会成为无源之水，无本之木。在一次数学辅导培优活动中，让学生做一道题：

已知：a，bcd均为实数，且c＞b＞a, 求：的最小值。

大部分同学都是根据绝对值的定义，用分类讨论法打开绝对值符号求解。就在大家肯定这种解法的正确性但理解和推导过程都非常复杂时，一位同学对大家说：“我的解法比你们的更简单易懂！”

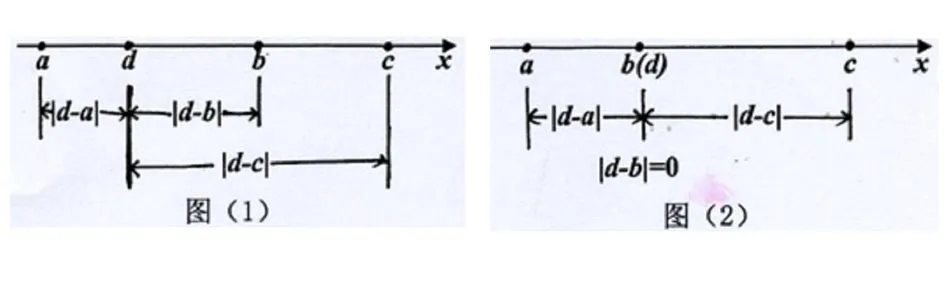
这是多么简捷、新颖，简直妙极了！充分体现了创新思维。

二、变式教学，培养创新思维

在数学教学中务必善于发掘教材基本题，在此基础上综合、变化、拓展、改造、深化，形成系列问题让学生探索，这对提高学生分析和解决问题的能力，发展智力等都起到事半功倍的作用。

三、运用构造法，培养创新思维

构造法是指从已知到未知的转化过程中，对已有知识和方法采取分解、组合、变化、类比、限定、推广等手段进行思维的再创造，构造出新的“数”与“形”来解题。

通过联想，利用均衡、对称、和谐进行构造，见解独到，不循常规，是培养创新思维的好途径。解答并不需要很多的基础知识，但让我们更感兴趣的是那些富有创造性的思想方法——构造法。

四、一题多解，培养创新思维

培养发散思维应着眼于研究未知事物，打破思维定势，拓宽视野、增广见识、开发智力、启迪创新思维的目的。现通过例题的一题多解，培养创新思维。

由此可知思维沿三条主线创新思考。

法1：如图（1），延长BC到D，使CD=AC，过A、C、D三点作圆，连AD，证AB是⊙ACD的切线。

法2：如图（2），延长AB到D，使BD=AB，过A、C、D三点作圆，交CB的延长线于E，证BE=BC+AC；又在BE上截取BF=BC，连DF，则再证。

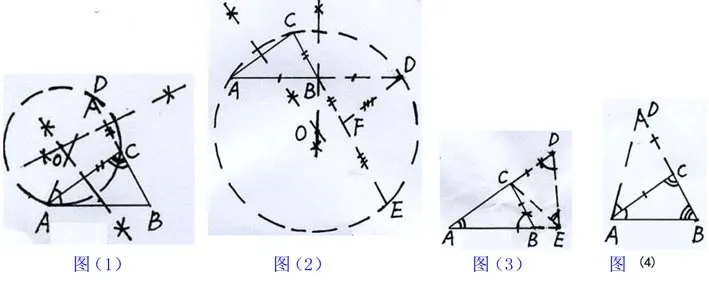
法4：如图（4），延长BC到D，使CD=AC，连AD，证明

法6：如图（6），以AB为直径作⊙O，又以B为圆心，BC为半径作⊙B交⊙O于D，交AC（或其延长线）于E，连AD、BD、BE，证AE=BE。

此外还可用平行线分线段成比例定理，或借助反映三角形边角关系的正弦定理和余弦定理。

另外，思维可由结论 ∠C= 2∠A出发逆向展开创新。

思路一：如图（7），由 ∠C= 2∠A想到作∠C的平分线，证明。

思路二：如图（8），由 ∠C= 2∠A想到在∠C内（或∠A上）作∠BCD（或∠BAD）=∠A（或=∠C），再证CD（或AC）是∠ACB（或∠BAD）的平分线。

由上可知，培养创新思维，学生必须具备扎实的基础知识，了解知识点间的联系和区别，熟悉各种知识的应用；教师要指导学生对已学知识进行总结，帮助他们沟通各知识系统间的联系，把知识点形成网络，随时调取所需知识进行创新。

五、精心设悬，培养创新思维

悬念是事物对人们心理造成的关切心情。教学中要根据学生的心理特点和思维规律，精心设置悬念，激发学生的学习兴趣，培养学生锲而不舍的创新精神。

设置悬念常有几种方式：

1、辨析谬误。错误往往是正确的先导，教学中要针对学生常犯的错误，设置悬念，寻求解决问题的“良药”并“对症下药”。

灵巧别致的悬念可以收到“一石激起千重浪”的良好效果，它扣击了学生的心扉，诱发强烈的求知欲，燃点创新思维的美妙火花，为课堂教学营造良好的艺术境界！

六、结语

创新是时代的主题，是中华民族伟大复兴的基石。这就迫切需要广大数学教师在教学中，注重培养学生主动探索、敢于实践、善于发现的科学精神，将创新的教材，创新的教法有机地结合起来，把培养学生的创新能力真正落到实处，使课堂真正成为著名教育家陶行知所说的“处处是创造之地，天天是创造之时，人人是创造之人”的创新摇篮，培养创新思维才能硕果累累。