提高学生解决问题方法的策略

广东省梅州市平远县黄畲中心小学 张祖坚

在新课程标准实验教材编写中，把“应用题”改为“解决问题”，这样做去掉脱离实际和机械模仿的内容。同时，也扩展了“解决问题”的实践特点体现了学生的创新探索精神和实践能力的教育理念。我在多年的数学教学工作中摸索总结出如下几种提高学生解决问题方法的策略：

一、运用分析法解决问题的策略

在数学解决问题中，分析法是从解决问题的结论或需求问题出发，一步一步地探索下去，最后达到题中设置的已知条件。即推理方向是：问题→已知。分析法的特点是：从问题入手，寻找解决问题的所需条件就是把研究的对象分解成它的各个组成部分，然后分别研究每一个组成部分，从而获得对研究对象的本质认识的思维方法，从“结论”探求“需知”，逐步靠拢“已知”，其逐步推理实际上是要寻找结论的充分条件。

例如，某农场有两个果园共30公亩，第一个果园收苹果3500箱，第二个果园收苹果2800箱，每箱苹果重100千克。平均每公亩收苹果多少千克？

图解分析法如下：

综合算式是：（3500+2800）×100÷30=2100（千克）

二、运用综合法解决问题的策略

在数学解决问题中，综合法是从数学题的已知条件出发经过逐步的逻辑推理，最后达到特证结论或需求问题。即推理方向是：已知→问题。而综合法的特点是：把认识对象的各个部分联系起来加以研究，从“已知”推出“可知”，逐步推向“未知”，其逐步推理实际上是要寻找已知的必要条件。

例如，AB两地相距600千米，甲乙两车从两地同时相向而行，10小后两车相遇，已知甲车开出后2小时行了50千米，乙车的速度是每小时多少千米?

1.文字综合法

①已知甲车开出后2小时行了50千米，求甲车的行驶速度。（50÷2=25千米/小时）②甲车相遇时10小时行驶了多少千米？（25×10=250千米）③相遇时乙车行驶了多少千米？（600－250=350千米）

④求乙车的速度。（350÷10=35千米）

根据上面的分析结果，综合算式是：（600－25×10）÷10=35（千米）

2.图解综合法如下

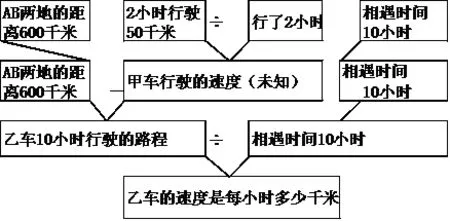
现在就可以引导学生根据图解分析的顺序列出综合算式：

（600－50÷2×10）÷10=35（千米/小时）

三、运用线段图解决问题的策略

在课堂教学中，我们除了教给学生分析法和综合法让学生去解决问题，还可以教给学生用线段图分析数量关系。用线段图分析数量关系在教学中更形象、具体，通过看图示中所标出的已知数量和未知数量就能推理出数量之间的关系，列出算式。在教学分数乘法和除法与行程问题的解决问题时，引导学生用线段图去分析数量关系，可以让学生结合题型去利用线段图分析、解决问题，学生也学得得心应手，用得轻松愉快。

四、运用代数知识解决问题的策略

在课堂教学中，培养学生的代数意识，为列方程解决问题打下坚实的基础。方程知识是“数与代数”知识的重要内容，用字母表示数则是掌握方程知识的基础，培养学生良好的代数意识非常重要。教师要充分认识到“用字母表示数”这部分知识的重要性。在课堂教学中，培养学生寻找等量关系的习惯，为列方程解决问题创造条件。能否正确列出方程的关键是能否正确找出等量关系。但是要正确找出等量关系并不容易，需老师长期引导和潜移默化教给学生一些寻找等量关系的方法。要求学生经过长期的训练，学生找等量关系的能力就会明显提高，就算遇到一些稍复杂的问题，也会一步步地分析，找出不同的等量关系，进而寻求解决问题的方法，要求学生记住一些常见的等量关系式。如“单位‘1’的量×分率=分率对应的量”“速度和×相遇时间=同时行的路程”以及一些面积和周长计算公式等等。在解决问题的过程中，激励学生用方程和算术等多种方法解决问题。这样不仅体现了课标提出的“算法多样化”，让学生在对比中提高分析和解决实际问题的能力。

例如，我在教学甲乙两车同时从相距500千米的两地相对开出，4小时后没有相遇，还相距20千米，已知甲车每小时行65千米，乙车每小时行多少千米？

在教学这道题时，让学生用算术方法解答，结果全班学生列出的算式有4种之多，但是只有少数学生列出了正确的算式。我就要求学生自己找等量关系，列方程解答，结果绝大多部分学生列出了正确的方程，求得了正确结果。当我问学生前后为什么会有这样呢？让学生说出思维方法：算术方法要“倒着”思考，而列方程是“顺着”想的，所以觉得要简单些。这就是我们经常说的“逆向思维”与“顺向思维”问题。列方程解决问题多数情况下是“顺向思维”，更符合学生的思维习惯，便于问题的解决。

在小学课堂教学中，解决问题的策略很多。对于小学生来说，一要基础，形象具体，适用面宽；二要适宜小学生学习，与他们的数学知识、生活经验相接近，与他们的思维发展水平相接近，带有趣味性。让学生能在愉快的课堂教学中，轻松获得知识，就能在学习的道路上不断奋发进取。