壁面温度分布的高超声速平板边界层稳定性分析及转捩预测

刘 璐, 曹 伟

(天津大学 力学系, 天津 300072)

0 引 言

高超声速飞行器是航空航天技术领域研究和发展的重点，有许多关键问题亟待解决，其中之一就是如何准确预测高超声速边界层的转捩位置[1-2]，因其直接影响到气动力、气动热计算的准确性，这是高超声速飞行器设计的基础。

在航空工业领域，eN方法被认为是预测转捩位置的最有效方法，其中，N值往往结合实验和飞行数据给出。但高超声速风洞实验存在诸多难点，且早期eN方法忽略了多种因素影响，如今正在逐步完善[3-4]。Chen等[5]对Ma=3.5条件下尖锥和平板模型的转捩现象进行了研究，发现绝热壁条件下测量得到的N=10的转捩预测位置与线性理论结果吻合良好。Malik[6]也用eN方法对Ma=3.5条件下尖锥转捩位置进行了研究，并将N值调整为5，这与一般公认的N=9～11相差甚远。苏彩虹等[7]指出了传统eN方法的不足并进行了改进，建议N值取为3.5。

在高超声速飞行器边界层稳定性分析以及转捩预测相关研究中，壁面一般采用绝热或等温条件。在不同壁面条件下，贾文利[8]研究了考虑真实气体效应对高超声速钝锥边界层稳定性及转捩位置的影响。研究发现：对于绝热壁条件，转捩位置随马赫数增大而推后；对于等温壁条件，在相同壁面温度下，转捩位置随马赫数增大而提前；在相同马赫数下，随着壁面温度降低，第一模态更加稳定，且壁面温度条件对稳定性产生影响，进而影响转捩位置；壁面温度冷却对第二模态扰动具有不稳定效应[9]。1984年，Mack[10]指出：与不可压缩流动边界层相比，超声速边界层存在多个不稳定模态；当马赫数大于4时，第二模态最不稳定。在来流马赫数Ma=8条件下，Stetson等[11-12]以半锥角7°的尖锥为模型，研究了壁面温度等对锥体稳定性的影响，得到了与Mack一致的结论；将通过水冷系统冷却的尖锥与非冷却尖锥的数据进行对比，发现冷壁使转捩雷诺数减小、转捩位置提前。苏彩虹等[13]在零迎角小钝度球头锥边界层转捩问题的研究中指出：虽然第二模态增长率远大于第一模态，但其增长区范围短，并不总是对转捩起决定性作用；壁面温度条件对转捩位置影响较大，对于等温壁情况，转捩由二维的第二模态主导，而绝热壁情况则由三维的第一模态主导。曹伟[14]通过对平板边界层转捩的研究发现，无论等温壁或绝热壁，在来流马赫数为8、10、12时，转捩均由第二模态主导。因此，转捩究竟由何种模态主导，仍有待深入研究。

Kendall[15]曾对超声速和高超声速边界层转捩进行了系统研究，发现距离尖锥尖端由近及远的4个热电偶测得温度各不相同，表明实际壁面温度既非等温亦非绝热。壁面温度条件直接影响基本流剖面、扰动演化特性、流动稳定性和转捩位置，只有得到符合实际流动的壁面温度，边界层稳定性分析和转捩预测才能得到符合实际的结果。因此，壁面采取何种条件也是值得研究的问题。

实际飞行中，等温壁面条件只适用于飞行初始阶段。随后，由于边界层内气动加热，壁面温度逐渐升高，沿流向各站位温度不再相等。长时间飞行后，壁面温度趋于定常；但由于壁面存在传热，绝热条件并不严格满足，壁面温度沿流向仍有一个分布。如何得到不同时刻壁面温度分布，并将其作为壁面温度条件用以预测转捩，是相关研究的关键所在。

针对薄壁超声速流动(Ma=3～10)，文献[16]提出了对流换热系数计算公式，并根据实际飞行器材料热物性，得到了任一时刻壁面温度分布。本文利用此方法得出壁面温度分布，通过直接数值模拟计算出基本流场，并分析其稳定性；采用eN方法预测转捩发生位置，与等温和绝热壁面温度条件的稳定性分析以及转捩预测结果进行对比；研究了求取某一时刻壁面等效温度作为等温壁面条件的壁温、并以之代替壁面温度分布条件进行稳定性分析和转捩预测的可行性。

1 数值方法

1.1 基本流的计算

其中，x、y分别为流向及法向坐标，U为流向速度，α、ω分别为流向波数和无量纲圆频率(下文简称频率)。

采用两种方法计算了Ma=4.5条件下、t=6.63s时刻的基本流：第一种方法是壁面采用对流换热公式，通过直接数值模拟从初始时刻计算到t=6.63s时刻的基本流；第二种方法是求得t=6.63s时刻壁面温度分布后，以之作为壁面边界条件，通过直接数值模拟得到定常的基本流。图1为两种方法得到的基本流对比(x= 0.6m处的法向速度、温度剖面、中性曲线和N值曲线的对比)，可以看出两者吻合很好。由于第二种方法更为省时，本文采用该方法得到基本流并进行稳定性分析。其详细计算方法为：

(a) 速度

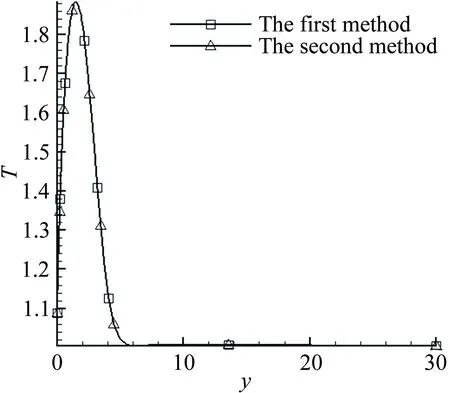
(b) 温度

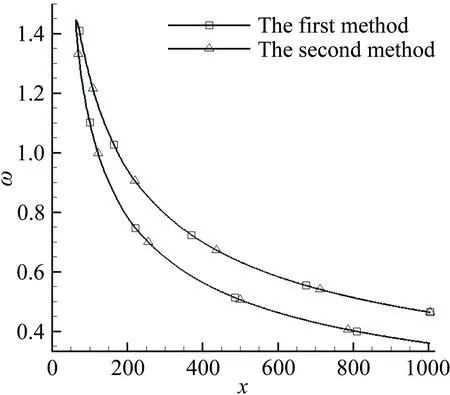
(c) 中性曲线

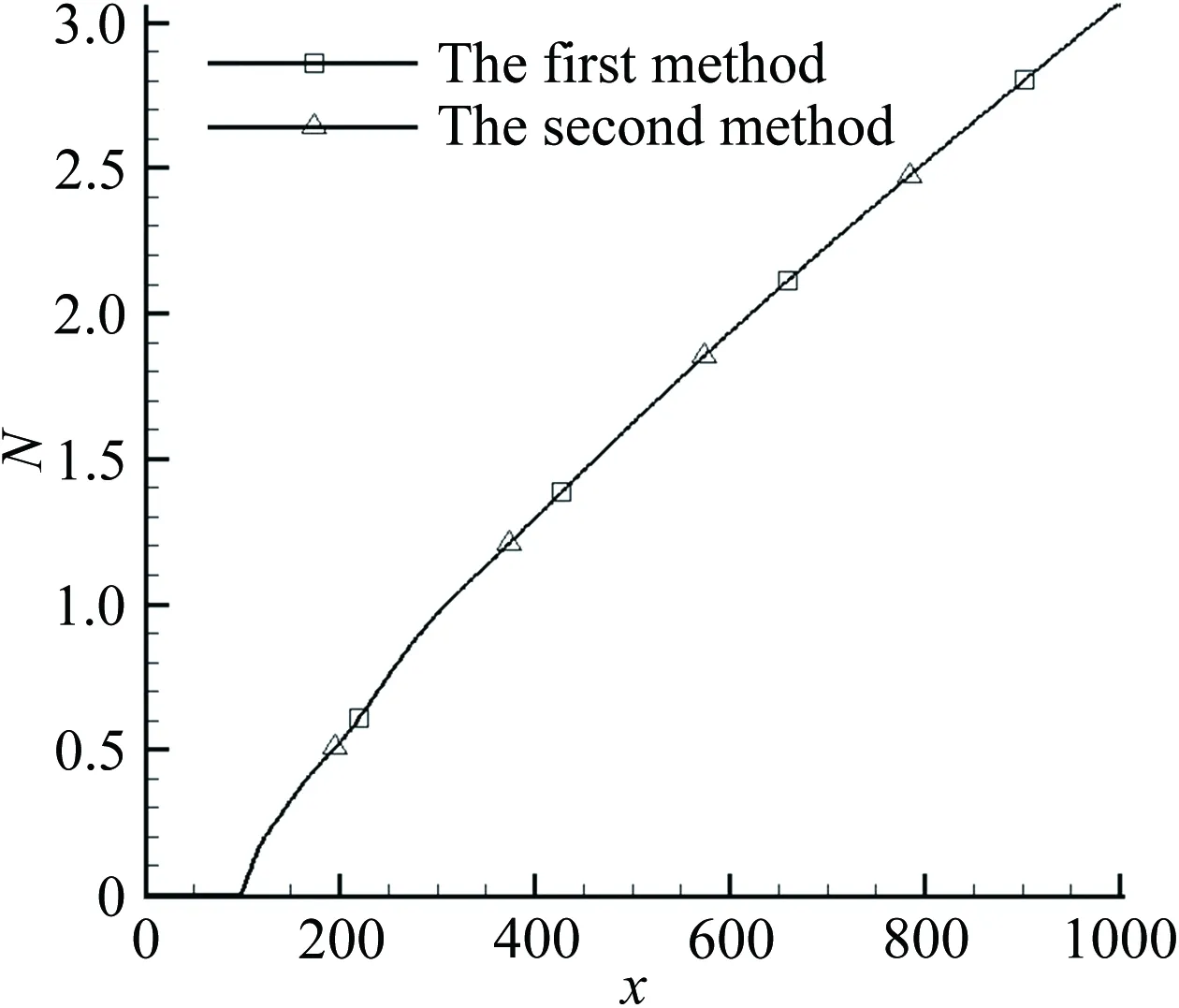
(d) N值曲线

Fig.1Comparisonofthebaseflowcomputedbytwodifferentcalculationmethods

用埃克特[17]参考焓方法求得平板上不同流向位置的对流换热系数：

(1)

其中，hx为局部对流换热系数，Pr=0.72，Tw、Hw为壁面温度、壁面焓，Tr、Hr为恢复温度、恢复焓。Tr、Hr可由经验公式获得。ρ*、μ*为参考焓H*下的密度和粘性系数。

对于超声速流动，固壁与气体间的局部对流换热满足传热公式：

qw=hx(Tw-Tr)

(2)

qw为热流密度。将式(1)代入式(2)，可得热流密度为：

(3)

平板壁面温度增加量ΔT用集总参数法求得：

(4)

壁面温度Tw可由来流温度与壁面温度增加量对时间的积分相加得出[16]：

(5)

c、ρ为金属平板的比热容、密度，δ为平板厚度的1/2，三者取值分别为520J/(kg·K)、4.7×103kg/m3和1mm。t表示在流场中经过的时间，S、m分别表示所计算平板模型的面积和质量。

图2给出了马赫数为4.5、6.0和7.0时、4个不同时刻(120、300、400和600s)的壁面温度分布，以及等温壁面温度(取来流温度)和绝热壁面温度沿流向的分布曲线。可以看出：等温和绝热的壁面温度沿流向不变；4个不同时刻的壁面温度，越靠近前缘温度越高。在t=120s时刻，Ma=4.5时，前缘温度接近绝热温度，Ma=6.0和7.0时，前缘温度达到绝热温度；对于其他3个时刻，前缘温度都已达到绝热温度。在4个时刻，温度都沿流向逐渐降低，且随时间增加，逐步向绝热温度分布线一侧靠近。

将式(5)得到的壁面温度作为直接数值模拟的壁面温度条件，分别计算马赫数为4.5、6.0和7.0时、不同时刻(120、300、400和600s)壁面温度分布的基本流场。等温和绝热的基本流场可直接由数值模拟(或相似性解)方法求得。

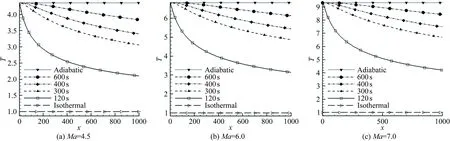
图2 不同壁面温度条件下的温度分布曲线

1.2 转捩预测方法

小扰动的演化可以用线性稳定性理论来研究，而eN方法就是基于线性稳定性理论的转捩预测方法[18-19]。根据线性稳定性理论，小扰动部分可以写为行波形式：

φ′=φ(y)ei(αx+βz-ωt)

(6)

其中，φ=(U,V,W，T,p)，V、W分别为法向及展向速度，φ′为对应的扰动量，z为展向坐标，β为展向波数。对于时间模式，α和β为实数，ω为复数，ω的虚部对应于扰动幅值沿时间的增长率；对于空间模式，β和ω为实数，α为复数，α虚部的相反数为扰动幅值沿流向的增长率。

eN方法中的N为幅值放大因子，定义为：

(7)

其中，A为小扰动幅值，A0为扰动初始幅值。对于高超声速情况，目前还没有系统的实验给出大小合适的N值作为转捩判据。因此，根据文献[7]和[20]，取扰动初始幅值为0.3‰，以幅值达到1.5%作为转捩开始位置，代入式(7)求得N≈4。

对于第二模态，其展向波数β=0，下文给出的N值曲线为不同频率扰动波增长曲线的包络线；对于第一模态考虑的是三维波，由于展向波数β不为0，因此，对不同展向波数、不同频率的扰动波增长率进行积分，找出这些扰动波最早达到e4的N值曲线。

2 壁温沿流向分布对基本流、流动稳定性及转捩位置预测的影响

2.1 不同壁面温度条件对基本流剖面的影响

图3给出了Ma=6.0、x=4m处、3种不同壁面温度条件(等温、绝热、壁面温度分布)下的法向速度剖面。可以看出：在不同壁面温度条件下，边界层中的速度不同，其中，等温壁面温度条件下，边界层中的速度最大，速度边界层最薄；绝热壁面温度条件下，边界层中的速度最小，速度边界层最厚。壁面温度分布条件下，边界层中的速度居中；在计算的4个时刻，边界层内同一法向位置的速度随时间增加而减小，边界层厚度增大。

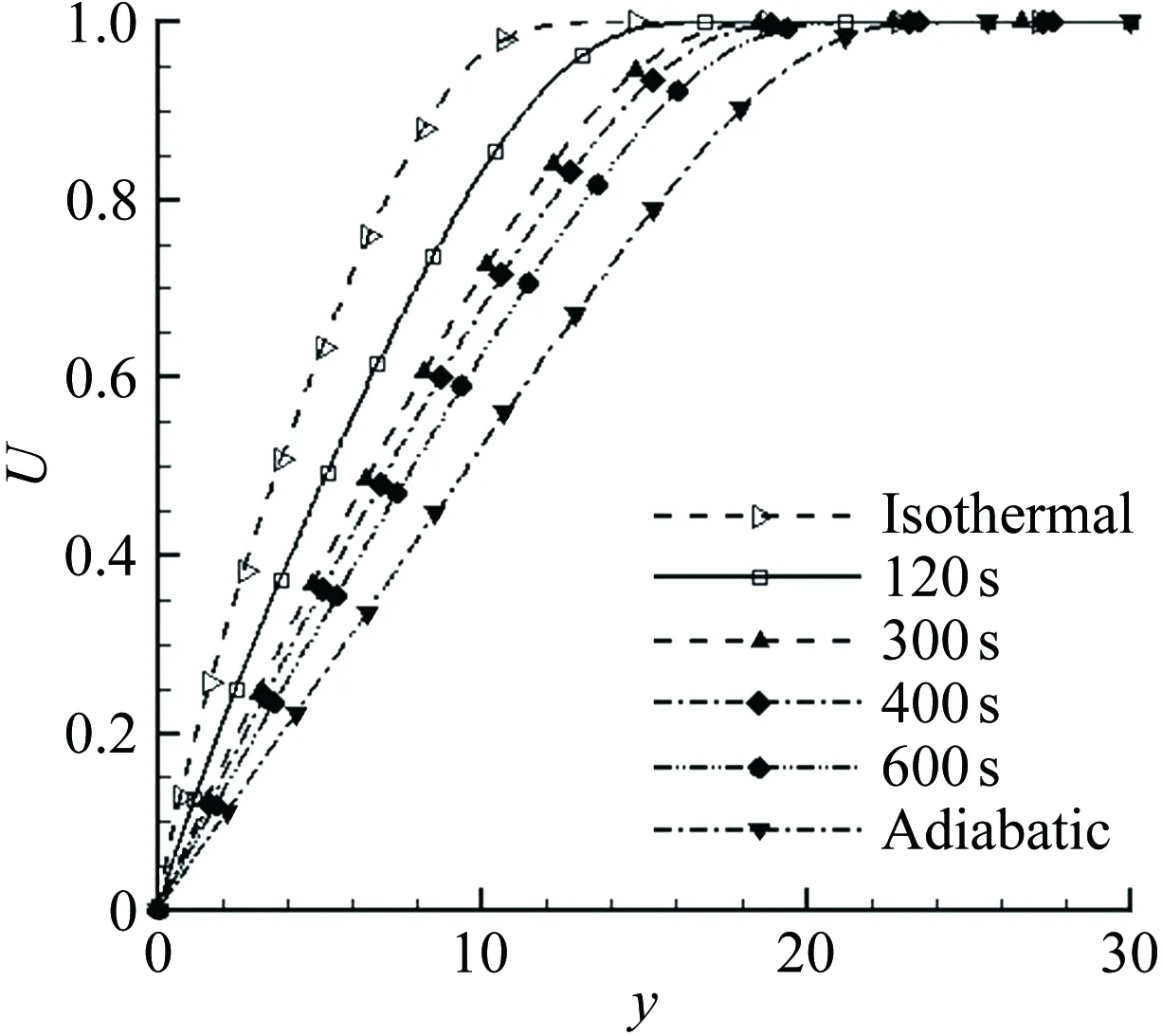
图3 不同壁面温度条件下的速度剖面

图4给出了Ma=6.0、x=4m处、3种不同壁面温度条件下的法向温度剖面。与法向速度剖面类比，可以得到相似结论：绝热壁温度最高，等温壁温度最低；温度分布条件边界层内同一法向位置的壁面温度随时间增加而升高，并逐渐接近绝热壁面条件的温度剖面。

Ma=4.5和7.0时的影响规律与此相同，从略。

图4 不同壁面温度条件下的温度剖面

2.2 不同壁面温度条件流动稳定性及转捩预测的结果比较

图5分别给出了马赫数为4.5、6.0、7.0时、不同壁面温度条件下(壁面温度分布的壁面条件以120s时刻代表，下文同)二维的第一和第二模态的中性曲线对比。图中，横坐标为中性曲线上的点到平板前缘的距离，即流向坐标；纵坐标为不稳定波的频率(图6同)。可以看出，在相同流向位置，基本流的壁面温度条件不同，中性曲线对应的不稳定区间频率范围不同。其中，绝热壁面中性曲线对应的不稳定区间频率较小，不稳定区出现的临界位置离平板前缘距离较远；等温壁面中性曲线对应的不稳定区间频率较大，范围也比较大，不稳定区出现的临界位置离平板前缘较近；壁面温度分布条件的中性曲线对应的不稳定区间频率在等温和绝热壁面温度条件之间，不稳定区出现的临界位置也在等温和绝热壁面温度条件之间。

图6分别给出了壁面温度分布条件下、马赫数为4.5、6.0和7.0时、4个时刻二维的第一和第二模态的中性曲线比较结果。可以看出，不同时刻壁面温度分布条件的中性曲线相同流向位置对应的不稳定区间范围也不同，随着时间增加，不稳定区间向低频方向移动，越来越靠近绝热一侧。马赫数越高，随着时间增加，第一模态越早出现。时间越靠后，第一模态越靠近平板前缘，不稳定区间也越大。

由图5、6可以看出，在绝热壁面条件下，中性曲线第一模态的不稳定区间比其他条件下更大，即壁面加热使第一模态的不稳定区间变大；随马赫数增大，第二模态不稳定区间逐渐与第一模态接近，直至重叠；在等温壁面条件下，没有找到第一模态的中性曲线。

以马赫数4.5的情况为例，给出不同壁面温度条件下、x=0.6m处、三维的第一模态和二维的第二模态增长率随频率的变化曲线，如图7所示。可以看出，第一模态增长区随时间增加而增大，在绝热壁面温度条件下的增长区最大。在等温壁面温度条件下，已很难找到第一模态增长率随频率的变化曲线；第二模态的增长区随时间的增加而减小。在等温壁面温度条件下的增长区最大。无论何种壁面条件，第二模态的最大增长率都大于第一模态的最大增长率，并且绝热壁面温度条件下第二模态的最大增长率与第一模态的最大增长率之比最小，对于等温壁则相反。可以得出如下结论：第一模态在绝热边界层中最不稳定；第二模态在等温边界层中最不稳定；在壁面温度分布条件下，时间越长，第一模态越不稳定，第二模态越稳定。

图5 不同壁面温度条件下的中性曲线

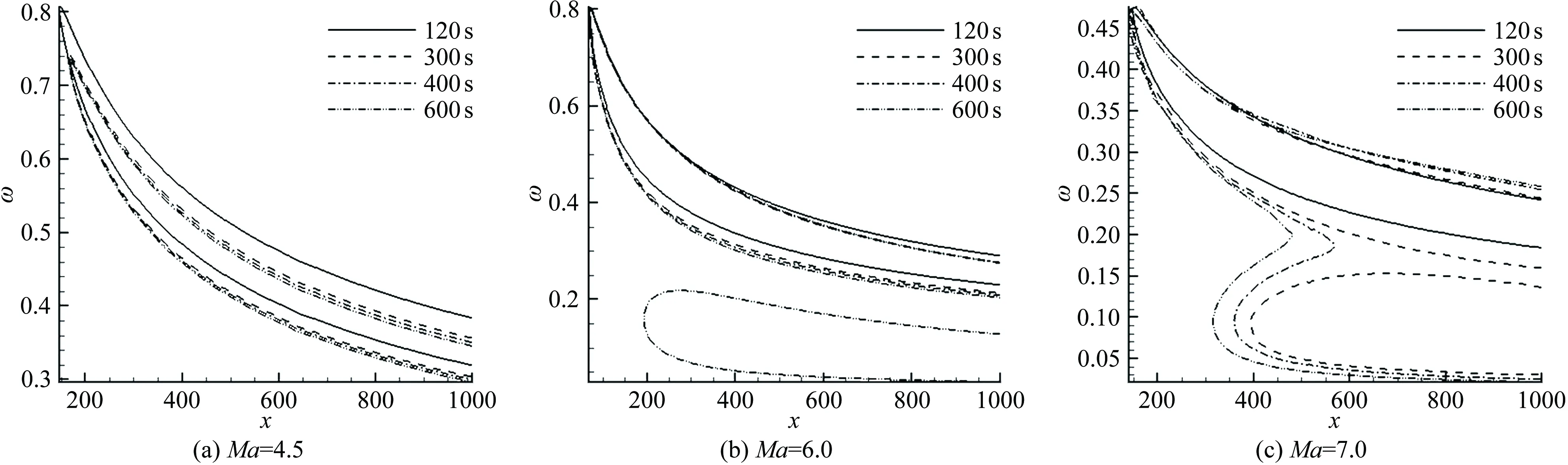
图6 壁面温度分布条件下不同时刻的中性曲线

(b) 第二模态

Fig.7Variationofgrowthratewithfrequencyunderdifferentwalltemperatureconditions

即壁面冷却使得第二模态更加不稳定、第一模态更加稳定。Ma=6.0和7.0的规律与此相同，从略。

图8、9分别展示了Ma=4.5、6.0和7.0时、不同壁面温度条件下N值曲线对比，以及壁面温度分布条件下不同时刻的N值曲线对比。同时，图中给出了三维的第一模态幅值放大倍数大于等于e4的情况。在Ma=4.5、6.0和7.0时，等温壁面温度条件下的转捩位置比绝热和壁面温度分布条件下的更靠近平板前缘，由第二模态主导转捩，且马赫数越大，位置越靠前；而在绝热壁面温度条件下，马赫数越大，转捩位置越靠后。Ma=4.5和6.0时，转捩由第一模态主导，Ma=7.0时，转捩由第二模态主导；在壁面温度分布条件下，转捩位置都由第二模态主导，相同马赫数下，随着时间增加，转捩位置越来越靠后；同一时刻，随着马赫数增大，转捩位置提前。Ma=7.0、不同时刻的N值曲线对比则比较特殊，300s之后的N值包络线都出现在300s的N值曲线左侧，转捩位置也都在300s之前，且随着时间增加、温度升高，转捩位置越来越靠前。分析认为：这种情况与400s以及大于400s时第一、二模态的中性曲线的交叉重叠有关。表1列出了不同壁面温度条件的平板边界层转捩位置。

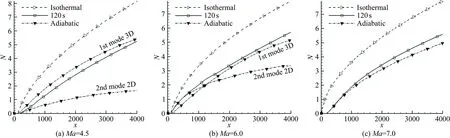
图8 不同壁面温度条件下的N值曲线

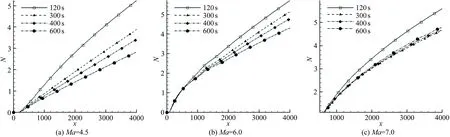
图9 壁面温度分布条件下不同时刻的N值曲线

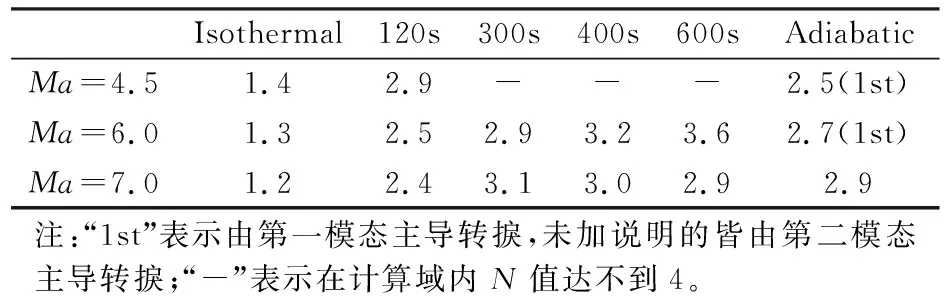
Isothermal120s300s400s600sAdiabaticMa=4.51.42.9---2.5(1st)Ma=6.01.32.52.93.23.62.7(1st)Ma=7.01.22.43.13.02.92.9注:“1st”表示由第一模态主导转捩,未加说明的皆由第二模态主导转捩;“-”表示在计算域内N值达不到4。

从表1可以看出，第二模态主导等温和壁面温度分布边界条件的转捩位置，即壁面温度低的第二模态更不稳定；第一模态在绝热壁面条件、Ma=4.5和6.0的情况下主导转捩，即壁面温度高的第一模态更不稳定，且转捩位置较第二模态明显提前。

对某一时刻，若能通过求取等效温度作为等温条件的壁温，直接求得相似解以代替壁面温度分布的基本流，而后进行稳定性分析及转捩位置预测，这样就可以简化计算、节省计算时间。为此，以Ma=7.0、120和300s时刻的平均温度(将壁面温度积分，再除以流向长度，得到平均温度)为例，分别以3.86和6.05倍的来流温度作为等温条件的壁面温度来计算的基本流，与120和300s壁面温度分布壁面条件的基本流得到的N值包络进行比较，结果发现两者相差较大，如图10所示。

(a) t=120s

(b) t=300s

Fig.10ComparisonofenvelopecurvesofNvaluesfortwobaseflows

选取若干不同温度作为等温壁面条件的壁温，直接求得相似解，将其作为基本流场，与采用温度分布通过直接数值模拟计算出的基本流场，分别进行稳定性分析及转捩位置预测。结果发现，这两种方法得到的N值曲线有较大差异，难以找到一个可以与壁面温度分布等效的壁温。

3 结 论

(1) 对于Ma=4.5、6.0和7.0的超声速、高超声速平板边界层而言，壁面温度越接近绝热壁温度，第一模态越不稳定，第二模态越稳定。在Ma=4.5和6.0的绝热壁面温度条件下，主导转捩的是第一模态，其余情况转捩均由第二模态决定。

(2) 壁面边界条件对转捩位置预测的影响很大。等温壁面条件下的不稳定频率最高，转捩位置较其他情况最靠近平板前缘，且马赫数越大转捩位置越靠前；绝热壁面条件下的不稳定频率最低，马赫数越大，转捩位置越靠后；壁面温度分布条件下，平板的壁面温度越接近绝热壁温度，不稳定区间越向低频方向移动，且转捩位置更靠后。与等温壁面温度条件类似的是，马赫数越大，转捩位置越靠前。需要指出的是，在Ma=7.0条件下，在400s以及大于400s时，第一和二模态发生重叠，故不完全满足上述规律。

(3) 对于壁面温度分布的边界条件，很难找到某一个温度作为等温壁温来代替。根据现有计算结果，仍需利用不同时刻的壁面温度分布作为壁面边界条件，通过直接数值模拟来获得基本流。