基于改进EMD的滚动轴承故障特征提取方法
2018-02-12高彩霞吴彤付子义
高彩霞 吴彤 付子义


摘要:针对滚动轴承早期故障信号微弱、背景噪声强、故障特征难以提取的特点,提出一种基于包络谱灰色关联度改进的经验模态分解(Empirical Mode Decomposition,EMD)特征提取方法。首先,用EMD将原始振动信号分解成若干本征模函数(intrinsic mode function,IMF)分量,计算原始信号及分解后各阶IMF分量的包络谱;然后,用灰色关联度分析计算原始信号包络谱与IMF分量包络谱之间的关联度,以包络谱关联度大小筛选IMF分量进行加权;最后,对加权的IMF分量计算能量、峭度、偏度形成特征集,通过主元分析(Principal Component Analysis,PCA)降维后输入概率神经网络(Probabilistic Neural Network,PNN)进行故障状态识别。该方法利用包络谱灰色关联度有针对性地筛选出对故障特征敏感的IMF分量,相比于单纯利用线性关系大小筛选IMF分量的相关性分析更具针对性。对滚动轴承4种故障状态早期故障信号进行识别,准确率为97.5%,表明该方法是有效的。
关键词:滚动轴承;故障识别;经验模态分解;灰色关联度
Fault State Recognition of Rolling Bearings Based on Envelope Spectrum Gray Correlation Degree Improved EMD, PCA and PNN
GAO Cai xia,WU tong,FU Zi yi
(School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454000, China)
Abstract:Aiming at the characteristics of early failure of rolling bearing with weak fault signal, strong background noise and difficulty in extracting fault features, an improved EMD (empirical mode decomposition) feature extraction method based on the grey relational degree of envelope spectrum is proposed. First, the original vibration signal is decomposed into several intrinsic mode function (IMF) components using EMD to calculate the envelope spectrum of the original signal and its decomposed IMF components; then the grey relational analysis is used to calculate the original degree of correlation between the signal envelope spectrum and the IMF component envelope spectrum by screening the IMF component with the size of the envelope spectral correlation; finally, the energy, kurtosis, and skewness of the weighted IMF component are calculated to form a feature set through the main Principal Component Analysis (PCA) which reduces the dimension and inputs Probabilistic Neural Network (PNN) to identify fault conditions. This method uses the grey correlation degree of the envelope spectrum to screen the IMF components that are sensitive to the fault feature. Compared with the correlation analysis, the IMF component can be screened more specifically by using the linear relationship size. The accuracy of the early fault signal recognition for the four fault states of the actual rolling bearing is 97.5%, which indicates the effectiveness of the method.
Key Words:rolling bearing; fault recognition; empirical mode decomposition; gray relational degree
0 引言
滾动轴承是各类旋转机械中的通用易损部件。据统计,旋转机械故障有30%是由轴承故障引起的,轴承的健康状态与机械能否正常运行息息相关,因此检测和诊断滚动轴承故障和故障位置十分重要。
近年来,EMD 方法被用于轴承的故障特征提取,但是该方法在分解原始信号形成IMF分量后,只有部分分量对故障敏感。如何选择有效的IMF分量是一个难点,故很多学者对IMF选取进行了研究。张志刚等[1]利用灰色关联度与互信息剔除了IMF分量中的虚假分量;崔玲丽等[2]利用相关系数提取主要IMF分量;彭畅等[3]利用度量因子筛选最能表征故障信息的IMF分量并进行信号重构;雷亚国等[4]利用相关系数之间的关系设计敏感度评估算法,选择反应故障特征的IMF分量。
上述研究都是利用IMF与原始信号的相似性或线性关系筛选有效的IMF分量,适应性好但针对性不强。由于滚动轴承在运行过程中采集的信号常常伴随有背景噪声,而背景噪声对故障特征提取影响较大,如果仅仅依靠IMF分量与信号本身的相似性来筛选对故障特征敏感的IMF分量,可能会因为噪音等原因而错误地选择非敏感IMF分量。本文提出一种基于包络谱灰色关联度改进的EMD特征提取方法,运用该方法对滚动轴承4种状态(正常、内圈故障、外圈故障、滚动体故障)进行识别。首先,计算4种状态下轴承原始信号与每个IMF分量的包络谱,分别计算4种状态的原始信号和对应的IMF分量包络谱之间的灰色关联度,得出相应的关联度大小序列,取关联度序列中的前若干个IMF分量,使其关联度大小之和大于0.9,并计算出关联权重系数对IMF分量进行加权,最后计算加权后的IMF分量的能量、峭度、偏度,利用PCA降低故障特征集维数并输入PNN进行故障识别。
1 基于包络谱灰色关联度的EMD方法
1.1 EMD方法原理
经验模态分解方法能根据信号自身的特点把一个复杂的多分量调制信号,按频率由高到低顺序分解成一组单分量调制信号,它不需要预先指定基函数,能自适应选择频带和带宽,具有自适应的多分辨率。
分解过程[5 7]:①确认原信号X(t)的所有局部极大值与极小值点,形成上下包络线并取均值m 1(t),得到信号与局部均值的差:h 1(t)=X(t)-m 1(t)。若h 1(t)满足IMF条件[8],则取h 1(t)为第一个IMF量,若不满足,则使h 1(t)成为新的X(t)。重复上述步骤,直到满足条件得到第一个内禀模态函数c 1(t);②分解出第一个IMF后,将原信号X(t)减去c 1(t),得到剩余的值r 1(t),使其继续重复上述步骤,依次得到第2个、第3个IMF分量,分别记为c 2(t)、c 3(t),一直到最后得到的r n(t)为单调函数。整个处理过程在满足预定的筛选停止准则后停止。
1.2 IMF选取方法
对信号进行EMD分解可以自适应得到一系列不同时间尺度的IMF分量和一个单调函数,使非平稳信号平稳化[9-10]。在利用EMD的故障识别方法中,早期认为前几个IMF分量是有用的,而后面的分量是虚假或是与故障无关的分量,具体选择依靠经验。后来有学者提出利用相关性分析方法分析原始信号与IMF分量的线性关系大小,借此筛选敏感IMF分量。但是相关性分析是分析原始信号与分量的线性关系,对于早期故障信号微弱的滚动轴承故障诊断来说,不免针对性不足。还有学者利用互信息、灰色关联度等手段筛选敏感IMF分量,但是缺点都与相关性分析相似。针对这种情况,本文提出一种基于包络谱灰色关联度的IMF选取方法。
包络谱对轴承故障非常敏感,可以十分清晰地看到因故障冲击所形成的峰值,即在轴承故障的特征频率处会出现谱峰,且与频谱相比包络谱的谱线清晰简单。
灰色关联度是灰色关联分析方法描述系统各因素之间关联程度的量化指标[11 13],是聚类算法的一种。此方法与相关性分析不同之处在于它是分析两组变量之间的变化态势,而不是线性关系。将包络谱与灰色关联度相结合,分析原始信号包络谱与IMF分量包络谱的变化态势,可有针对性地筛选出故障特征敏感的IMF分量。
基于包络谱灰色关联度的IMF选取方法如下:
(1)计算第一种状态原始信号的包络谱数据X o={x o(j)j=1,2,3,···,n},及对应的IMF分量包络谱数据X k={x k(j)k=1,2,3,···,m;j=1,2,3,···,n}。
(2)计算第一种状态下IMF 1,IMF 2,···,IMF m包络谱与原信号包络谱之间的灰色关联度R 1,R 2,···,R m。
计算包络谱之间的关联系数α k(j)为:
其中λ为分辨系数,λ∈(0,1],它的取值与分辨率成反比,本文取0.05以符合数据要求[14]。
对关联系数求平均值得到灰色关联度
{y 1 n} 越大,表明它们的包络谱关联性越大,反之亦然。
(3)灰色关联度由大到小依次排列,得到关联度序列 {y 1 k} 。
(4)計算相邻两个关联度大小的差。
(5)找出对应最大差值的索引作为 k 1。
(6)重复前面5步,找出第2、3、4种状态的索引k 2,k 3,k 4。
(7)比较k 1,k 2,k 3,k 4 大小,取最大值为全局关联IMF分量个数K。
(8)对预测数据进行计算得到关联度序列{ y k} ,取其对应的前K个IMF分量的灰色关联度求和:
预测IMF x(x=1,2,···,K)分量的关联权重系数为:
上述公式中,右上标为轴承状态编号。
应用上述敏感IMF筛选方法选出IMF分量并加权后,即可进入后续步骤。
2 滚动轴承故障特征提取
信号特征参数选择是非常关键的一步,一般从统计特征中选择,包含均值、标准差、方差、偏斜度、峭度、 峰峰值、方根幅值、平均幅值、峰值、 波形指标、峰值指标、脉冲指标、裕度指标等。选择的参数如果太多会形成过高维度的向量组,不方便计算,选择太少又会使故障信息遗漏,所以要对症下药,选择既适合滚动轴承振动信号的特征参数,又能快速便捷地计算特征量。早期学者使用能量信息作为特征参数,基于EMD的内禀模态能量法[15 17]就是其中之一,但是当出现故障因素以外的较大冲击时,故障状态识别会出现误差。所以本文增加两个特征量,分别为信号的峭度与偏度,以辅助能量参数,弥补故障特征信息缺失。
峭度指标是无量纲参数,由于它与轴承的转速、尺寸、负载没有关系,所以具有很好的适应性,而且它对冲击信号特别敏感,适用于表面的点蚀损伤类故障。一般正常轴承的峭度指标接近于3。
而偏度指标反映了振动信号的不对称性,表示信号概率密度函数中心偏离标准正态分布的程度,反映信号幅值分布相对其理想均值的不对称性,除了有急回特性的机械设备外,如果存在某一方向的摩擦或者碰撞,就会造成振动波形的不对称,使偏度指标增大。
采集滚动轴承4种故障状态进行实验,采用基于包络谱灰色关联度的EMD方法,对加权IMF分量提取能量(E)、峭度(K)、偏度(S)特征参数后输入PNN进行状态识别,结果如表1所示。
由表1可以看出,单个能量作为特征参数识别准确率略低,但增加了峭度、偏度两个参数后,识别准确率得到明显提高。
3 主元分析
主元分析是多元统计分析中常用的方法,与基于傅里叶体系下的方法、频域分析方法有着本质区别,它的特点是同时处理多个维度变量数据,从这些数据中发掘出隐藏的统计信息特征,很好地消除不同维度之间的相关性,使多个相关变量转化为少数几个独立变量,即用相对于原始特征集较少维度的新特征集反映原本数据该有的大部分信息。主元分析还能消除故障数据中的噪声和冗余,提高准确性[18 20]。
主元分析法的基本原理是构造原始数据X的线性组合Y:
满足Y 1、Y 2、Y m之间的独立性,Y 1、Y 2、Y m对应的方差依次递减。主要步骤参考文献[18],其中X为提取能量、峭度、偏度后形成的特征集,Y 1,Y 2,···,Y m为形成的主元。根据分析得出的单个主元贡献率,以及前若干个主元累计贡献率选择主元数量。
本文因为采用全局关联IMF分量选择方法,所以会产生较高维度的故障特征集。为了提高故障识别效率以及正确率,采用主元分析降低故障特征集的维度。
4 实验分析
为验证本文故障诊断方法的有效性,采用来自美国凯斯西储大学电气工程与计算机科学系的实验室数据[21],实验装置如图1所示。
图1的左边是实验电机,中间是扭矩传感器,右边是测力计。
实验采用加速度传感器,它放置于电机外壳的驱动端和风扇段,本文采用驱动端数据,采样频率为12kHz,实验对象为SKF6205-2RS深沟球轴承,轴承的故障是由电镀技术加工而成的单点故障,数据的内圈故障特征频率为162.4Hz,外圈故障特征频率为107.5Hz,滚动体故障特征频率为141.4Hz。电机在2马力下取得数据,分别有内环故障数据、外环故障数据、滚动体故障数据以及正常轴承数据,上述4种数据组成本次实验的原始数据。
从原始数据中,选取1 024个数据作为一组。上述4种状态,每种状态选择40组,总共160组数据,其中每个状态随机选择10组作为训练组,其余30组作为测试组。识别流程如图2所示。
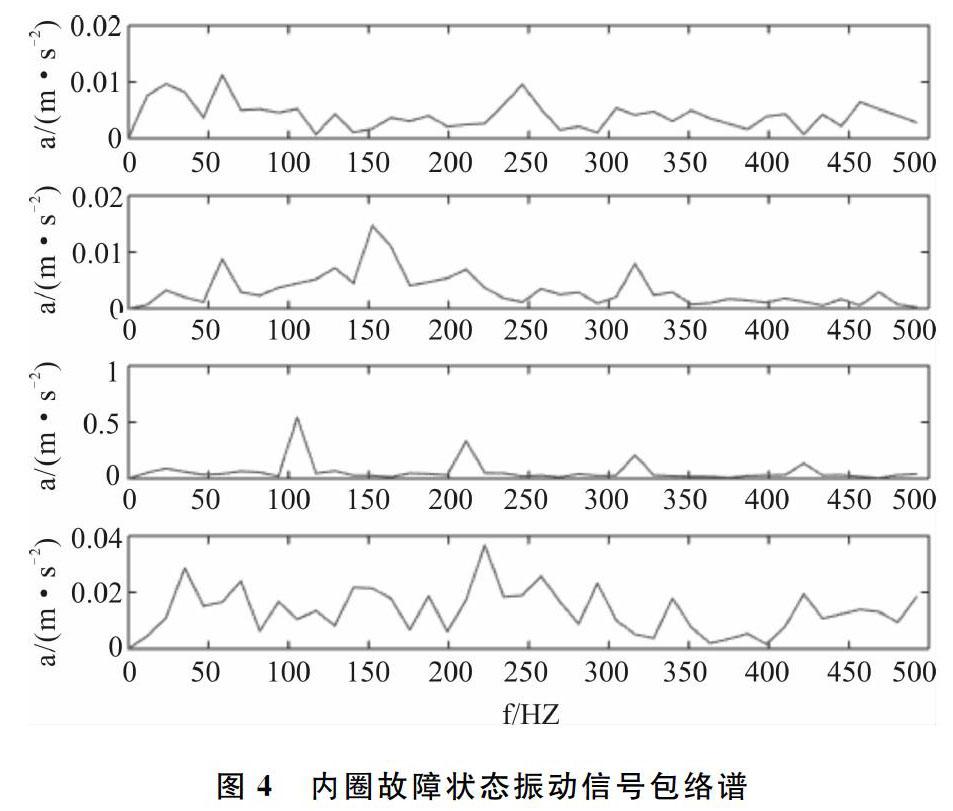
图3、图4依次是正常状态、内圈故障状态、外圈故障状态、滚动体故障状态的原始振动信号与包络谱。从包络谱可以看出,在内圈故障特征频率处有峰值,外圈故障特征频率的峰值更加明显,而滚动体在故障特征频率处却不能明显看出存在峰值。但因为包络谱简洁清晰的特性,在筛选IMF分量时会选取与原始信号相似度高的IMF分量,减少选择无效IMF分量可能性。
图5为外圈故障信号的IMF分量包络谱,以关联度序列排序,其关联度从上到下逐渐降低。可以看出从图5第4个IMF分量包络谱开始,在故障特征频率处已经不能明显看到峰值,说明后续分量已经不适合选择为故障特征敏感的IMF分量。
以包络谱灰色关联度方法筛选IMF分量后,计算其能量、峭度、偏度特征参数形成故障特征数据集,然后进行主元分析,最后输入到PNN中进行状态识别。主元分析见表2。
一般主元分析累计贡献率达到85%就可保留绝大部分原始信息[8]。从表2可以看出,从第5个主元开始,累计贡献率就达到了88.9%以上,满足了对原数据集降维的要求。
将主元分析后的数据依次输入到PNN中进行状态识别,结果如圖6所示。
从图6可以看出,当取一个主元时,正确率93.3%,随着主元的增加,正确率有所提高,在取4、5个主元时达到最大值97.5%。随后在取10个主元后,稳定在95.8%。
再依据表3,综合考虑取4个主元为最终方案,这样既可保证正确率,又能得到更高的效率。
将本文方法与相关性分析方法、灰色关联度方法、互信息方法筛选IMF分量作比较。相关性分析方法选择大于0.3的分量进行重构,灰色关联度方法选择关联度之和大于0.9的分量,互信息方法与灰色关联度一样,最后选择合适的主元,得到表4的结果。
从表4可以看出,运用不同筛选方法后PNN所用时间相差无几,说明它们筛选的IMF分量在数量上基本一致;但正确率却相差很大,说明不同筛选方法所选择的IMF分量不同。包络谱灰色关联度正确率最高,达到97.5%,说明此方法有针对性地选择出了对故障特征敏感的IMF分量。
5 结语
(1)在基于EMD的滚动轴承故障诊断方面,相比于用相关性分析、灰色关联度、互信息等方法筛选IMF分量,运用包络谱灰色关联度来筛选对故障特征敏感的IMF分量更具针对性,效果也更好。
(2)从最后结果来看,本文提出的基于包络谱灰色关联度改进的EMD方法,能够有效提取故障特征并对滚动轴承的4种故障状态进行识别。
参考文献:
[1] 张志刚,石晓辉,施全.基于改进EMD和谱峭度法滚动轴承故障特征提取[J].振动、测试与诊断,2013,33(3):478 482.
[2] 崔玲丽,高立新,张建宇. 基于EMD的复合故障诊断方法[J].北京科技大学学报,2008,30(9):1055 1060.
[3] 彭畅,柏林,谢小亮. 基于 EEMD、度量因子和快速峭度图的滚动轴承故障诊断方法[J].振动与冲击,2012,31(20):143 147.
[4] 雷亚国. 基于改进 Hilbert Huang 变换的机械故障诊断[J].机械工程学报,2011,47(5):72 77.
[5] 郑祖光,刘莉红. 经验模态分析与小波分析及其应用[M].北京:气象出版社,2010.
[6] 冷军发,荆双喜.EMD与同态滤波解调在滚动轴承故障诊断中的应用[J].河南理工大学学报:自然科学版,2014,33(5):612 615.
[7] 席旭刚,武昊,罗志增. 基于EMD自相关的表面肌电信号消噪方法[J].仪器仪表学报,2014,35(11): 2494 2500.
[8] 裴峻峰,毕昆磊,吕苗荣. 基于多特征参数和概率神经网络的滚动轴承故障诊断方法[J].中国机械工程,2014,25(15):2055 2058.
[9] 董振华,李芳,姜愉. EMD以及类EMD方法[J].软件导刊,2014,13(10): 37 39.
[10] 席旭刚,武昊,罗志增. 循环平稳信号EMD去噪分解的局限性研究[J].软件导刊,2014,13(12): 33 35.
[11] 安学利,周建中,刘力.基于熵权理论和信息融合技术的水电机组振动故障诊断[J].电力系统自动化,2008,32(20):78 81.
[12] 张文斌,郭德伟,普亚松.谐波窗分解样本熵与灰色关联度在转子故障识别中的应用[J]. 中国电机工程学报,2013,33(21):132 137.
[13] 卢绪祥,苏一鸣,吴家腾. 基于EMD及灰色关联度的滑动轴承润滑状态故障诊断研究[J].动力工程学报,2016,36(1):42 47.
[14] 申卯兴,薛西锋,张小水.灰色关联分析中分辨系数的选取[J]. 空军工程大学学报:自然科学版,2003,4(1):67 70.
[15] 于德介,程军圣,杨宇.机械故障诊断的Hilbert Huang变换方法[M].北京:科学出版社,2006.
[16] 王錄雁,王强,张梅军.基于EMD的滚动轴承故障灰色诊断方法[J]. 振动与冲击,2014,33(3):197 202.
[17] 向丹,岑健.基于EMD熵特征融合的滚动轴承故障诊断方法[J]. 航空动力学报,2015,30(5):1149 1150.
[18] 梁晴晴,韩华,崔晓钰. 基于主元分析 概率神经网络的制冷系统故障诊断[J].化工学报,2016,67(3):1023 1031.
[19] 欧璐,于德介.基于监督拉普拉斯分值和主元分析的滚动轴承故障诊断[J].机械工程学报,2013,50(5):88 94.
[20] 王宏超,陈进,董广明.基于补偿距离评估 小波核PCA的滚动轴承故障诊断[J].振动与冲击,2013,32(18):87 94.
[21] LOPARO K A.Bearings vibration data set,Case Western Reserve University[EB/OL].http://www.eecs.cwru.edu/laboratory/Bearing/download.htm.
