一类改进Chua系统隐藏吸引子研究
2018-02-12袁运李庶民
袁运 李庶民
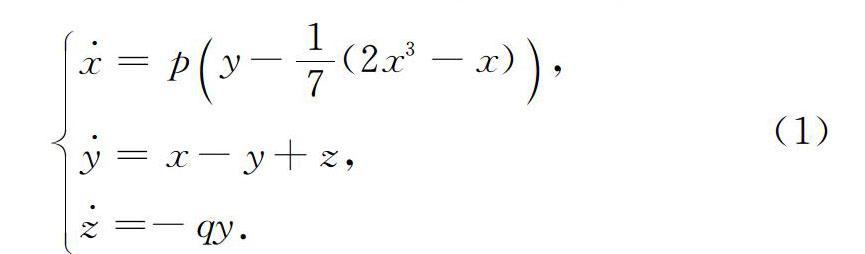


摘要:对一类改进的Chua系统进行定位系统的隐藏吸引子研究。首先,通过对改进的Chua系统平衡点稳定性进行分析,确定系统在一定条件下有一对纯虚特征根。由于存在一对纯虚特征根,系统在平衡点处就会出现Hopf分支。然后,通过描述对原系统进行变换,以引入一系列连续函数序列对系统进行解析数值算法迭代,与定位稳定周期解的谐波线性化方法结合定位原系统的隐藏吸引子。通过MATLAB数学软件进行数值模拟得到系统的Lyapunov指数谱和分岔图,从而为隐藏吸引子的存在性提供依据。运用相关程序在MATLAB的帮助下制作出系统的隐藏吸引子相图,得出在这类改进的Chua系统中存在隐藏吸引子的结论。
关键词:平衡点;改进Chua系统;Hopf分支;解析数值;谐波线性化;隐藏吸引子
Hidden Attractor of a Modified Chua System
YUAN Yun, LI Shu min
(College of Science, Kunming University of Science and Technology, Kunming 650500, China)
Abstract:Firstly, by discussing the stability of the equilibrium point of the improved Chua system, we can determine that the system has a pair of pure imaginary eigenvalues under certain conditions. By describing the transformation of the original system and introducing a series of continuous function sequences to iterate the analytical numerical algorithm of the system, and combining with the harmonic linearization method to locate the stable periodic solution, the hidden attractor of the original system is located. Then, the Lyapunov exponential spectrum and bifurcation diagram of the system is obtained by numerical simulation with MATLAB software, which provides the possibility for the existence of hidden attractor. Then, with the help of Matlab, the phase diagram of hidden attractor is obtained. Finally, it is concluded that hidden attractor exists in this improved Chua system.
Key Words:equilibrium point; modified Chua system; Hopf bifurcation; analytical numerical; harmonic linearization; hidden attractor
0 引言
過去几十年来,动力系统的吸引子是一个热门研究课题。众多学者研究了经典的Lorenz[1]、Chua[2]、Rossler[3]、Chen[4]系统等著名系统的普通吸引子。这类吸引子都是由不稳定平衡点激发的(自激吸引子),在某些动力系统[5 6]中能够从Hopf分支中得到稳定的极限环和混沌吸引子。研究这些吸引子需要用一种标准的数值方法,从平衡点邻域中不稳定流形上的一点出发,经过一段时间的轨道运行得到吸引子并确定它。
Leonov等[7 9]提出隐藏吸引子概念,给出一整套找到隐藏吸引子的新的数值分析方法,并率先发现Chua系统中存在隐藏吸引子,通过数值模拟得到其轨线。这项研究结果昭示了有别于典型吸引子(如Lorenz、Chua、Rossler、Chen系统中的吸引子)的另一类吸引子。这类吸引子的吸引域不包含平衡点邻域,且不能用研究经典吸引子的方法得出这类吸引子。因此,对隐藏吸引子的局部数值计算和分析研究很难。Leonov等[10 13]研究的Chua系统提出并使用了一类特殊的解析数值方法定位隐藏吸引子,并通过数学方法得到隐藏吸引子的几何形态。随着Leonov等人对于隐藏吸引子的研究,一些学者开始在Chua系统基础上进行各类隐藏吸引子存在性研究。
Yassen [14]研究了其中一种改进的Chua系统:
其中, p>0和q>0是系统(1)的系数,x和y表示通过两个电容器的电压,z 表示通过电阻的电流,Yassen主要利用这一系统研究自适应控制和自适应同步。
本文将Yassen的Chua系统(1)作了改进,变为如下更一般的系统:
其中, α,β,μ,ν,l均是正数。当μ=17,ν=2,l=1时,系统(2)就是系统(1)。将α 作为分支参数研究系统(2)的Hopf分支。与系统(1)相比,系统(2)有相对复杂的动力学性质,包括周期轨道和隐藏吸引子。
1 不变性、平衡点与Hopf分支
1.1 对称性与不变性
在坐标变换 (x,y,z)→(-x,-y,-z) 下,系统(2)保持不变,即系统(2)关于原点对称。
1.2 平衡点稳定性分析
当 α,β,μ,ν,l均为正数时,系统(2)有3个平衡点:O(0,0,0),S ±±νν,0,l·νν。
平衡点O和S ±的稳定性如下:
(1)平衡点O 所对应的特征方程如下:
其中, p 1=1-αμ,q 1=β-αμ-lα,r 1=-αβμ ,式(3)可以写为:
由 α,β,μ,ν,l均为正数可知r 1<0,p 1,q 1 不一定大于0。根据Routh-Hurwitz判据可知,平衡点 O(0,0,0)不稳定。
(2)在坐标变换(x,y,z)→(-x,-y,-z)下,系统(2)保持不变,从而系统(2)关于原点对称,因而对于S ±的稳定性只需考虑S +的稳定性即可。
作线性变换x-=x-νν,y-=y,z-=z+l·νν,系统(2)变为:
系统(2)的平衡点S +,其实就是系统(5)的平衡点 O (0,0,0),它所对应的特征方程为:
令 p 2=1+2αμ,q 2=β+2αμ-lα,r 2=2αβμ ,式(6)变为:
由Routh-Hurwitz判据可得到:
引理1 由于p 2>0,r 2>0,若p 2q 2-r 2>0,则方程(7)的特征根具有负实部。
定理1 平衡点S ± 渐进稳定,当且仅当特征方程(7)的根具有负实部。
引理2 若系统(2)出现Hopf分支,则特征方程(7)有一个实根 λ 1=-(2αμ+1),和一对共轭纯虚根λ 2,3=±ωi(ω>0)。
1.3 Hopf分支
由于平衡点 O(0,0,0)不稳定,因此只需讨论从S ±分岔出的周期轨。等式(7)至少有一个负根,若等式(7)有一对共轭纯虚根λ=±ωi(ω>0),代入方程(7)可分离出虚部与实部, ω 满足:
将α作为分支参数,因而临界值α c满足f(λ 1)=f(-(2αμ+1))=0,即
整理后得:
注意到 α>0,得到以下结论:
(1)当2μ=l时,式(9)无正根。
(2)当2μ>l时,式(9)的两个根α 1,α 2同号,且均为负根。
(3)当2μ<l时,式(9)的两个根α 1,α 2异号,且其中一个为正根。
由此可知,当2μ<l时,方程(9)有正根,且
其中Δ=( 2μ-l) 2-8βμ(2μ-l)。
若2μ<l,当α<α c时,方程(7)有一对纯虚根λ=±ωi,从等式(7)中可得:
将λ(α c)=iω代入式(11)中得:
从式(8)的第二个等式可以得到:
所以β>ω 2。若2μ<l成立,则
从而得到定理2。
定理2 若 2μ<l,且α c由式(10)定义,当α经过α c时,系统(2)在平衡点S ± 处经历Hopf分支。
2 隐藏吸引子定位算法
利用文献[7 13]的算法定位系统(2)的隐藏吸引子。
2.1 算法思想
系统如下[15 17]:
其中,Ρ是n×n阶常数矩阵,q和r是n维向量,是转置,ψ(σ)是标量函数,且ψ(0)=0。
定义谐波线性化系数k,使矩阵
具有一对纯虚特征值λ=±ω 0i(ω 0>0),且其余特征值均具有负实部。假设k存在,则原系统(12)变为
其中 φ(σ)=ψ(σ)-kσ。
可引入一个有限的连续函数序列φ 0(σ),φ 1(σ)…φ m(σ),且每相邻两个函数φ j(σ)与φj+1(σ)的差别较小,函数φ 0(σ)的值最小,且φ m(σ)=φ(σ)。
由于函数φ 0(σ)最小,因此对系统进行谐波线性化:
确定一个稳定的非奇异的周期解 x 0(t)。
为确定出原系统(12)的吸引子,随着j的增大对周期解x 0(t)進行逐步演化,记x 0(t)为Α 0的起始振荡吸引子(不包含平衡点的吸引子)。此时可能会存在两种情况:
(1)Α 0的所有点都位于Α 1的吸引域中,Α 1是系统
在 j=1的情形下的振荡吸引子。
(2)当系统(15)过渡到j=1时的系统(16)时,由于不稳定分支破坏周期解而导致Α 0消失。
在第(1)种情况下,把x 0(0)作为初始点计算当j=1时系统(16)的解x 1(t)。如果x 1(t)不会趋近于平衡点,同样也不会趋近于无穷远(要考虑充分大的程序运行区间[0,T]),则x 1(t)进入到吸引子Α 1中。再执行j=2时系统(16)的情况,将x 2(0)=x 1(T)作为初始点,经过充分长的一段运行时间t之后得到当j=2时系统(16)的解x 2(t)。
继续执行以上程序,且逐渐增大j,取x j(0)=xj-1(T)为初始点,可找到当j=m时系统(16)(即原系统(12))的解x j(t),或在运算某一步中不稳定分支破坏周期解。
2.2 稳定周期解定位算法
由于要充分考虑到系统[18 20]中存在非线性项,所以将系统(14)改写为:
其中,Ρ 0是n×n阶常数矩阵,q和r是n维向量,φ(σ)为连续函数且满足φ(0)=0,k为谐波线性化系数,使得Ρ 0有一对纯虚特征根λ=±ω 0i(ω 0>0),其余均有负实部。
通过非退化线性变换,可将系统(17)化简为:
其中 y 3,b 3,c是n-2维向量,b 1,b 2为实数;A是(n-2)×(n-2) 阶矩阵,其余特征根均具有负实部。
系统(17)的变换函数为:
系统(18)的变换函数为:
其中η,θ为实数,Q(p)为n-2次多项式,R(p)为低于n-2次的多项式。设Q(p)与R(p)没有相同的根。由于系统(17)和(18)等价,则变换函数(19)与(20)相等,得到如下关系式:
定义描述函数
定理3[8 9] 若存在一个正数a 0,使a 0满足:
对于充分小的ε>0,则系统(17)具有初始条件x 0(0)=S(y 1(0),y 2(0),y 3(0)) 的周期解x 0(t),其中
y 1(0)=a 0+O(ε),y 2(0)=0,y 3(0)=O n-2(ε),且O n-2(ε)是n-2维向量,其它分量为O(ε)。
定理3保证了通过谐波线性化方法结合迭代算法寻找稳定周期解的可行之处,也保证了定位隐藏吸引子的可能性。
采用上述算法思想[15 17,20]定位系统(2)的隐藏吸引子。首先将系统(2)改写为类似系统(12)的形式:
其中
接着考虑引入谐波线性化系数 k和一个小参数ε ,并把系统(21)改写为如下形式:
其中
并且矩阵 Ρ 0的特征根满足:
λΡ 0 1,2=±iω 0,λ 3=-d<0
通过非退化线性变换 x=Sy ,可将系统(23)转化为如下形式:
其中
A=0-ω 00 ω 000 00-d,b=b 1 b 2 1,u=1 0 -δ
系统(22)的变换函数 W H(p) 可以表示为:
由于系统(22)与系统(23)具有等价性,因此可得到系统(23)的变换函数:
W H(p)=r (Ρ 0-pI)-1q
其中 p是复变量,且初始振荡频率ω 0 由公式lm W H(iω 0)=0决定,谐波线性化系数k由公式k=-( Re W H(iω 0))-1决定,则得到以下关系式:
由于系统(23)是系统(21)通过非退化线性变换x=Sy得到的,因此矩阵S满足:
设矩阵
于是可得:
s 11=1,s 12=0,s 13=-δ
s 21=-(μ+k),s 22=-ω 0α,s 23=δ(d+α(μ+k))α
s 31=-βα,s 32=β(μ+k)ω 0,s 33=βδ(d+α(μ+k))dα
对于充分小的ε,可得到以下初始值:
作为定位隐藏吸引子算法的第一步初始值,由式(25)可得系统(22)与系统(23)的初始值之间的关系为:
再回到系统(2),可以确定其初始值为:
其中a 0可由描述函数Φ(a)确定,描述函数满足Φ(a 0)=0且dΦ(a)da a=a 0≠0。
3 数值模拟
分别取l=1.4,μ=0.25,ν=6和β=300 。利用MATLAB软件可作出相应的相图,最大值法可画出系统的分支图,且Lyapunov指数谱可由Wolf[21]中提到的程序得到。
3.1 由不稳定平衡点出现的吸引子
当取上述参数值时,系统(2)有3个平衡點, 分别为O(0,0,0)和S ±(±0.408 2,0,0.571 5)。前述已得出O(0,0,0)总是不稳定的,通过简单计算,可以看到2μ=0.5<l=1.4,因而可以得到临界值α c=24.839 2在系统(2)中有两个纯虚特征值。平衡点S ±在α∈(0,α c)稳定,且在α>α c上失去稳定性。当α>α c 时,系统(2)将呈现更为复杂的动力学行为。
圖1显示对于系数α系统(2)的Lyapunov指数谱。当 α ∈(10,24.839 2)时,最大的Lyapunov指数总为负值。且由图2中可见,当 α ∈(10,24.839 2)时,从S ±中不能分支出周期轨且S ±总是稳定的。
当 α ∈(24.839 2,50)时,最大的Lyapunov指数接近于零,意味着系统(2)有周期轨。图2显示当 α过渡到α c=24.839 2时,能从S ±中分支出周期轨,且当α ∈(50,80)时,最大的Lyapunov指数总是为正值。这表明随着α值的增大,系统(2)通过分支达到混沌。
注意所有的吸引子都是从平衡点分支而来,因此计算吸引子需要从平衡点的小邻域中的某一初始值去计算。
3.2 隐藏吸引子
在上述的数值模拟中,吸引子是在平衡点S ±的邻域中不稳定流形上的一点出发的。在图(3)中,通过上述算法可以探测出初始值,且由这些初始值出发的轨道不会缩减至 O或S ±。也就是说,吸引子不会在S ±的邻域中不稳定流形上的点开始,即吸引子是隐藏的。
(a)α=20 (b))α=30 (b))α=30
(c)α=65
图3(a)-图3(c)显示随着 α 值的变化隐藏吸引子的不同情况。图3(a)显示S ±稳定,且当 α=20时,隐藏吸引子围绕在S ±周围;图3(b)显示S ±不稳定,且当α=30时,隐藏吸引子围绕在S ±分支出的周期轨周围;图3(c)显示 S ±周围出现混沌,且当α =65时,隐藏吸引子围绕在混沌轨道周围。
从上面的数值结果可见,隐藏吸引子由平衡点分支而来。通过数值模拟能够定位并发现隐藏吸引子,即这个改进的Chua系统中存在隐藏吸引子。
4 结语
通过对改进Chua系统隐藏吸引子研究,可以看出这一系统符合解析数值算法,即引入一对连续的函数序列不断进行迭代,并利用无限逼近的方法逐渐接近原系统进而得到原系统的解。对于系统稳定周期解的定位其实就是对原系统进行非退化变换,得到的系统具有一对纯虚特征根,其余特征值均具有负实部。变换前后的函数对应值相同,并且通过谐波线性化得到稳定周期解,它的初始值必须满足定理3。通过MATLAB画出lyapunov指数谱、分岔图和相图,可以看出隐藏吸引子存在于这一系统中。
本文存在以下不足:对于隐藏吸引子存在于这一系统只是满足解析数值算法,无法在理论上证明出隐藏吸引子与平衡点邻域不相交。因此,针对隐藏吸引子与平衡点邻域不相交的问题是下一步研究的重点。
参考文献:
[1] LORENZ E N. Deterministic nonperiodic flow [J]. Journal of The Atmospheric Sciences, 1962(20):130 141.
[2] ROSSLER O E. An equation for continuous chaos[J]. Physics Letters A, 1976, 57(5): 397 398.
[3] CHUA L O, LIN G N. Canonical realization of chua's circuit family[J]. IEEE Transactions on Circuits & Systems, 1990, 37(7): 885 902.
[4] CHEN G R, UETA T. Yet another chaotic attractor[J]. International Journal Of Bifurcation & Chaos, 1999,9(7):1465 1466.
[5] QI G, CHEN G, DU S, et al. Analysis of a new chaotic system[J]. Physica A Statistical Mechanics & Its Applications, 2012, 352(2): 295 308.
[6] JING Z, YANG J, FENG W. Bifurcation and chaos in neural excitable system[J]. Chaos Solitons & Fractals, 2006, 27(1): 197 215.
[7] KUZNETSOV N V, LEONOV G A, VAGAITSEV V I. Analytical numerical method for attractor localization of generalized chua's system[J]. Ifac Proceedings Volumes, 2010, 43(11): 29 33.
[8] LEONOV G A, VAGAITSEV V I, KUZNETSOV N V. Algorithm for localizing Chua attractors based on the harmonic linearization method[J]. Doklady Mathematics, 2010, 82(1): 663 666.
[9] LEONOV G A, KUZNETSOV N V, KUZNETSOVA O A, et al. Hidden oscillations in dynamical systems[J]. Wseas Transactions On Systems & Control, 2011, 6(2): 54 67.
[10] LEONOV G A, KUZNETSOV N V. Analytical numerical methods for investigation of hidden oscillations in nonlinear control systems[J]. Ifac Proceedings Volumes, 2011, 44(1): 2494 2505.
[11] LEONOV G A, KUZNETSOV N V, VAGAITSEV V I. Localization of hidden Chua attractors[J]. Physics Letters A, 2011,375(23):2230 2233.
[12] LEONOV G A, KUZNETSOV N V, VAGAITSEV V I. Hidden attractor in smooth Chua systems[J]. Physica D Nonlinear Phenomena, 2012, 241(18): 1482 1486.
[13] KUZNETSOV N V, KUZNETSOVA O A, LEONOV G A, et al. Hidden attractor in Chua's circuits[C].8th International Conference on Informatics in Control, Automation and Robotics. 2011: 279 283.
[14] YASSEN M T. Adaptive control and synchronization of a modified Chua's circuit system[J]. Applied Mathematics & Computation, 2003, 135(1): 113 128.
[15] LEONOV G A, KUZNETSOV N V. Hidden oscillations in dynamical systems. 16 hilbert′s problem, Aizerman′s and Kalman′s conjectures, hidden attractors in Chua′s circuits[J]. Journal Of Mathematical Sciences, 2014, 201(5): 645 662.
[16] KUZNETSOV N V, LEONOV G A. Hidden attractors in dynamical systems: systems with no equilibria, multistability and coexisting attractors[J]. IFAC Proceedings Volumes, 2014, 47(3): 5445 5454.
[17] LEONOV G A, KISELEVA M A, KUZNETSOV N V, et al. Discontinuous differential equations: comparison of solution definitions and localization of hidden Chua attractors[J]. Ifac Papersonline, 2015, 48(11): 408 413.
[18] DUDKOWAKI D, JAFARI S, KAPITTANIAK T, et al. Hidden attractors in dynamical systems[J]. Physics Reports, 2016, 637: 1 50.
[19] LEONOV G A, KUZNETSOV N V. Hidden attractors in dynamical systems from hidden oscillations in Hilbert Holmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits[J]. International Journal Of Bifurcation & Chaos, 2013, 23: 1330002.
[20] TESI A, VICINO A. Robust absolute stability of lur'e control systems in parameter space[M]. Pergamon Press, Inc. 1991, 27(1): 147 151.
[21] WOLF A, SWIFT J B, SWINNEY H L, et al. Determining Lyapunov exponents from a time series[J]. Physica D Nonlinear Phenomena, 1985, 16(3): 285 317.
