基于炉膛结渣监测模型的吹灰优化
2018-02-08徐力刚黄亚继岳峻峰
徐力刚 黄亚继 王 健 岳峻峰 邹 磊 杨 钊
(1东南大学能源热转换及其过程测控教育部重点实验室, 南京 210096)(2江苏方天电力技术有限公司, 南京 211102)
作为锅炉的燃烧系统,炉膛内火焰中心温度极高,因而烟气飞灰成分中处于熔融软化状态且黏结性很强的灰粒易黏附在水冷壁管上形成结渣,如不及时清除会导致锅炉传热效果严重下降甚至造成停炉.虽然大型锅炉炉膛配有吹灰器进行清渣,但是由于缺乏炉内实时结渣的直观数据,大多数电厂根据经验制定的按时定量吹灰方式并不合理,或吹灰不足引起受热面传热性能下降,或吹灰次数过多导致蒸汽的浪费以及对受热面造成冲蚀.因此,如何建立炉膛结渣污染监测模型并基于实时监测结果制定合理的吹灰方案,成为大型火电机组需要解决的难题.
目前,国内外学者已在炉膛水冷壁结渣监测方面取得了一定成果.Ma等[1]通过CFD模拟炉膛内结渣的位置并与实测结果进行比对以验证模型,从而进行炉膛结渣位置的预判,但CFD模拟计算时间较长无法做到实时预测,不适用于实时结渣监测.Romeo等[2]通过建立神经网络模型训练大量离线参数预测实际监测结果,而神经网络方法要取得较好的结果需要大量的训练样本.Zhang等[3]和马美倩等[4]采用声学测温的方式获得炉膛出口烟温,从而建立结渣监测模型,在烟气介质变化较小的稳定工况下测量结果较好.俞海淼等[5]将热流计安装在水冷壁上进行结渣监测,而只有在炉膛各个部位都安装热流计监测结果才较为可靠,而热流计维护困难,因此该方法目前实际应用不多.总体来说,上述文献在如何根据实时监测结果从而指导合理吹灰操作方面的研究较少.
为此,本文首先建立炉膛结渣监测模型,通过实例计算分析结渣监测模型的适用性,并指出根据监测结果执行吹灰操作存在的问题.然后提出一种基于单位时间炉膛传热量最大的吹灰优化模型,进行吹灰优化实例计算,并与现有文献中的吹灰优化模型进行对比,最后制定吹灰优化方案.
1 炉膛结渣监测模型
1.1 结渣监测指标
本文采用水冷壁热有效系数ψ作为污染率的特征参数进行建模.污染率的表达式为
(1)
式中,F为结渣污染率;x为水冷壁角系数,即水冷壁占炉墙面积的比例;ψ为水冷壁热有效系数,表示辐射热交换热流量占火焰有效辐射热流量的比例.
从污染率定义可知,当水冷壁结渣越严重,水冷壁接收辐射热量占火焰投射热量份额越小,ψ越小,则F趋向于1;当水冷壁越清洁时,水冷壁接收辐射热量占火焰投射热量份额越大,ψ越大,则F趋向于0.污染率F变化趋势与炉膛水冷壁结渣程度相符,能够作为结渣监测的指标.
1.2 炉膛辐射传热模型
由式(1)可知,污染率F的主要参数是ψ,可以通过炉膛辐射传热模型计算获得.
文献[6-8]在建立炉膛结渣监测模型时均采用了经典热力计算标准[9]中的炉膛辐射传热模型,而此模型的假设条件为火焰中心紧贴水冷壁平面或者不考虑辐射介质对辐射的吸收及散射作用,但随着锅炉容量和体积的增大,炉膛的辐射传热模型需要考虑在传播过程中火焰辐射能的减弱[10],因此本文采用文献[11]的炉膛传热模型.
传热模型中炉膛传热量可以用两平面(水冷壁平面和假想火焰辐射平面)之间辐射换热量、炉墙吸收火焰辐射能量以及炉中烟气放热量来表示,公式如下:
(2)
(3)
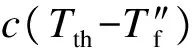
(4)

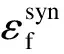
(5)
(6)
式中,εf为炉膛实际火焰黑度;ka为吸收减弱系数,m-1;R为与炉膛截面等面积圆形的半径,m.

(7)
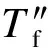
(8)
最后获得水冷壁热有效系数ψ的计算式,即
(9)
(10)
式中,xm为火焰相对高度;Z为本文方便推导求解公式所设过程参数,无实际意义.
1.3 基于烟温软测量的污染率计算方法


(11)
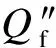



图1 半辐射受热面烟温测点
为简化计算,认为炉膛穿透屏区辐射全部被高温过热器吸收,即忽略穿透高温过热器向后的辐射量,则半辐射受热面的热平衡方程为

(12)
(13)

污染率计算流程图如图2所示.

图2 计算流程图
2 结渣监测计算实例及存在问题
为了研究监测模型对水冷壁实时结渣情况的适用性,本文以某600 MW超临界直流锅炉作为研究对象,锅炉型号为HG-1956/25.4-YM5,是一次中间再热、超临界压力变压运行直流锅炉.此锅炉采用Π型布置,单炉膛、平衡通风、固态排渣,旋流燃烧器采用前后墙布置,对冲燃烧.
从锅炉DCS系统中采集数据进行计算分析,采样间隔为2 min,现场记录实际吹灰操作时间.由于锅炉运行中存在各种扰动且热工参数变化时间较长,因此对采集数据使用最小二乘估计[14]的数据重构预处理方法来剔除坏值,以保证数据的连续准确性,采用多测点取平均值的方法来减少锅炉结构不均匀性所导致的误差.
2.1 实际运行工况结渣污染率计算
取一天(24 h)的数据,采用本文所建立的炉膛结渣监测模型进行实时结渣污染率计算,结果见图3.

图3 稳定负荷下炉膛结渣污染率
如图3所示,大部分时间内污染率的整体变化趋势非常明显.在进行吹灰器吹扫的时间段(8:00—9:20 和17:30—18:50)内,炉膛污染率有明显下降,与炉膛实际结渣减少相符,且吹灰时间80 min与实际程控时间相对应;而在不进行吹灰的时间段(0:00—8:00,9:20—17:30,18:50—24:00)内,污染率整体呈上升趋势,与炉膛实际结渣增加相符.因此可以认为,本文所建立炉膛结渣污染监测模型能够基本满足炉膛结渣监测的要求.
2.2 根据污染率进行吹灰存在的问题
炉膛结渣监测的最终目的是进行吹灰操作,目前文献中采用较多的方式是设定污染率的上下限,即临界污染率[15],当锅炉运行中炉膛实时污染率达到污染率上限时进行吹灰,达到污染率下限时停止吹灰.
根据临界污染率来判定吹灰时机及吹扫时间必须基于实时污染率曲线的稳定和准确性,当污染率曲线无法反映实时结渣情况时会导致吹灰误操作.如图3所示,虽然污染率的整体变化趋势非常明显,但是由于预处理不能完全消除热工参数的稳定和脉冲扰动,污染率数值随时间有小幅度的上下波动,这一情况会影响运行人员对吹灰操作的判断.除此之外,锅炉运行过程复杂多变,炉膛结渣监测模型由于是基于热平衡原理,在负荷变化过快的工况下结渣污染率的变化趋势会受到较大影响.图4为包含快速变负荷工况的结渣监测结果.在负荷较为稳定阶段(0:00—7:50,15:40—24:00),污染率变化趋势较为明显,吹灰时间段(16:20—17:40)内整体下降,不进行吹灰时污染率整体上升;而在快速变负荷阶段(7:50—15:40),炉膛污染率变化较为紊乱,除了在吹灰时间段(8:00—9:20)污染率整体呈下降趋势与结渣变化相符外,其他时间的污染率波动过大,不能反映实际结渣情况.因此,实际计算结果表明,在负荷变化过快情况下由于工质吸热存在滞后时间[13],炉内传热不平衡,炉膛结渣监测模型的适用性较差,污染率曲线不能够指导吹灰操作.

图4 包含变负荷工况下炉膛结渣污染率
根据结渣监测计算结果,锅炉实际运行中污染率曲线的波动不可避免,文献[2,16]也指出即使引入了神经网络等智能算法也只能减缓而无法消除快速变负荷下的污染率变化幅度.所以,仅根据实时污染率和临界污染率来执行吹灰操作的吹灰方案并不合理.
3 吹灰优化方案
目前大多数电厂采用按时定量的吹灰方案,即每天按照固定的时间进行相同时长的吹灰操作,形成一个固定的吹灰周期,但固定吹灰周期的制定只考虑运行人员排班而缺乏数据支撑,所以此方案有较大的弊端;而通过设定临界污染率来判定吹灰时机和吹扫时间的方式过于依赖实时污染率曲线的准确性,在运行工况变化复杂的情况下适用性较差.
基于以上情况,本文将临界污染率与按时定量吹灰周期相结合制定吹灰方案,在根据临界污染率判定吹灰时机和吹扫时间的同时辅以吹灰周期进行校核,从而确保不同工况下吹灰操作的合理进行.
3.1 吹灰优化模型
吹灰时机和吹扫时间需要通过建立吹灰优化模型进行求取,本文提出一种基于单位时间炉膛传热量最大的吹灰优化模型.
如图5(a)所示,结渣时间和吹灰时间综合为一个吹灰周期,其中Qj为结渣时间内的传热量变化曲线,Qc为吹灰时间内的传热量变化曲线,τj,τc分别为结渣和吹灰时长.由于Qj和Qc的变化趋势都是趋于平缓,因此通过合理调整吹灰周期内的τj和τc就可以使得单位时间内炉膛传热量QL最大.

(a) 炉膛传热量变化

(b) 炉膛污染率变化
此外,如图5(b)所示,其中Fj为结渣时的污染率变化,Fc为吹灰时的污染率变化,Qb(阴影部分)为吹灰带来的传热量收益,因为进行吹灰导致的能量损失随吹扫时长的增加而不断变大,所以吹灰获得的传热量收益必须要大于吹灰的能耗损失.因此,以单位时间内炉膛传热量QL最大为目标并加入一些约束条件,求解结渣时长τj和吹灰时长τc相当于一个非线性规划问题,吹灰优化模型为
maxQL=
(14)
(15)
式中,Qs为单位时间吹灰引起的蒸汽、电机及引风机能耗损失;Fmax,Fmin分别为临界污染率上、下限;τcmin,τcmax分别为吹灰程控最小、最大时间.
求解模型中,式(14)为目标函数,式(15)为约束函数,实际计算中需根据具体运行情况设定临界污染率下限Fmin.
3.2 计算实例和结果分析
本文对第2节中锅炉炉膛吹灰优化实例进行计算.由于炉膛污染率计算结果是离散值,不能直接运用于吹灰优化模型,需要进行曲线拟合.根据文献[17-18],Fj和Fc的拟合形式如下:
Fj=A-Be-Cτ
(16)
Fc=De-Eτ
(17)
式中,A,B,C,D和E都是拟合得到的常数,且都大于0.由于锅炉运行过程中热工参数受到的扰动极大,不同工况下计算出的τj,τc会不同,但是在相同负荷和煤种条件下的运行参数较为稳定.因此可以将电厂的运行过程划分成不同的常运行负荷及煤种工况,计算出每个工况下对应的τj,τc以及临界污染率,从而指导吹灰操作.以常运行负荷500 MW为例,为了提高数据拟合结果的拟合优度以及可靠性,采用多组相同运行负荷和煤种工况下污染率数据进行拟合,多组数据的衔接排列方法基于最优拟合优度的思想,方法见图6.

图6 多组污染率衔接排列方法
图7为8组(第1~8组)500 MW下Fj的排列和拟合结果,图8为4组(第a~d组)500 MW下Fc的排列和拟合结果.可以看出,多组污染率经过重新衔接排列后(见图7(a)和图8(a)),其按同一时间计算得到的污染率平均值随时间变化(见图7(b)和图8(b))的拟合结果较好,拟合优度在90%以上,能够较为准确地应用于吹灰优化计算.

(a) 8组结渣污染率随时间变化

(b) 结渣污染率平均值随时间变化及拟合曲线

(a) 4组吹灰污染率随时间变化

(b) 吹灰污染率平均值随时间变化及拟合曲线
为了满足约束要求Fc(τj)=Fj(τj),计算中将Fc拟合式变化为
Fc(τ)=0.824 45e-0.001 78(τ-τj+τm)
(18)
式中,τm是为了限定Fc拟合曲线起始点所设的中间参数,可通过式(15)消去.
将Fj和Fc的拟合结果代入吹灰优化计算模型,进行τj,τc以及Fmax的计算,此工况下设定临界污染率下限Fmin=0.68,τcmin=60 min,τcmax=108 min.通过求解式(14)和(15)的非线性规划问题,得到的计算结果见表1.

表1 吹灰优化计算结果(500 MW)
如表1所示,优化计算结果中吹灰频率提高,吹灰周期(τj+τc)从720 min降低到了279.74 min,单次吹灰时间从80 min减少到60.7 min,而单位时间炉膛传热量提高了67 611.3 kJ/min,相当于提高2.31 kg/min标煤的发热量,优化效果明显.
3.3 不同吹灰优化模型计算结果对比
目前较为常用的受热面吹灰优化模型主要有损失平衡模型[19]、最小损失模型[18]和最大收益模型[18].其中,损失平衡模型和最小损失模型定义实际和理想传热量(清洁时)之差为灰污染导致的热量损失.损失平衡模型认为灰污染损失一定要大于吹灰损失时才有吹灰意义,最小损失模型认为一定存在一个吹灰周期使得单位时间内总损失最小;而最大吹灰收益模型定义吹灰净收益为吹灰获得的传热量收益减去吹灰能量损耗,由于传热量收益增长的趋势会减缓,直到不变,故模型认为必然存在一个时刻使得吹灰操作获得的净收益最大.本文根据这几种模型进行了吹灰优化计算,并与本文吹灰优化计算模型的计算结果进行对比(工况条件与本文优化模型相同),结果见表2.
如表2所示,损失平衡模型和最小损失模型计算出的单位时间炉膛传热量较大,但是这2种模型的吹灰净收益为负,这是由于该模型的对比基准理论传热量(清洁时)在计算中不变,脱离了实际的污染率变化情况,使得一次吹灰的损失超过了获得的传热量收益;最大收益模型计算出的吹灰净收益最大,但是其单位时间炉膛传热量最小,这是由于该模型为了追求最大的吹灰净收益而基于受热面较脏(临界污染率上限较大)的前提,导致受热面可能较长时间处于传热效率较小的情况.此外笔者认为,对于最大收益模型,由于τj越大,炉膛越脏,获得的吹灰收益越大,当传热量收益较长时间达到不变(dQb/dτ=0)时,可能存在计算出的τj,τc时间太长的情况,需要酌情处理.
在混凝土铺盖北部有大块疑似空隙,铺盖中部偏西有小块异常,中部偏东及其南部也分散了数块异常区域;橡胶坝段西线中部有疑似空隙,东线有小面积的两块异常;最后钢筋混凝土防护坡中,南部塌空处往北延伸数米,有大块疑似空隙,距南部边缘20m靠近防护槽部分有异常,此异常以北有范围较大约8m的疑似空隙,防护坡北部各处也分散一些异常,面积较小。
综上所述,本文提出的基于单位时间炉膛传热量最大的吹灰优化模型,综合了上述几种模型的优点,计算结果较适用于锅炉实际吹灰操作.
3.4 吹灰优化方案
为了解决由于炉膛运行工况复杂且变化较快而污染率曲线波动较大不能反映炉膛内实时结渣的问题,本文将临界污染率、结渣时长τj和吹灰时长τc相结合制定吹灰优化方案,如图9所示.图中判断吹灰时间与τj和τc是否相近,可根据电厂具体要求决定,一般至少要达到τj和τc计算时长的2/3才可称为相近.此外,在负荷和煤种变化较小时电厂也可采用固定的τj和τc进行吹灰方案制定以减少运行人员的操作负担.

图9 吹灰优化方案
由于电厂实际炉膛吹灰操作中还需要兼顾主汽和再热蒸汽温度、过热器和再热器减温水流量、负荷标准和排烟标准等电厂指标,电厂实际吹灰方案可在本文制定的优化方案基础上进行修改.
4 结论
1) 提出了一种求解炉膛出口烟温以及炉膛污染率的方法,在炉膛出口烟温软测量计算中考虑了炉膛实时结渣情况.
2) 结渣监测实例计算表明,监测模型适用于负荷较为稳定的工况,而负荷变化过快工况下的监测结果由于波动较大不能作为吹灰操作判据.
3) 提出了一种基于单位时间炉膛传热量最大的吹灰优化模型,实例计算采用相同工况下多组污染率基于最优拟合优度原则进行衔接排列获得拟合曲线,结果表明在锅炉500 MW负荷下优化效果明显,能使炉膛提高相当于2.31 kg/min标煤的发热量.
4) 本文吹灰优化模型与现有文献中优化模型的对比结果表明,本文吹灰计算模型更适用于锅炉实际吹灰操作.
)
[2] Romeo L M, Gareta R. Fouling control in biomass boilers[J].BiomassandBioenergy, 2009,33(5): 854-861. DOI:10.1016/j.biombioe.2009.01.008.
[3] Zhang S P, Shen G Q, An L S, et al. Ash fouling monitoring based on acoustic pyrometry in boiler furnaces[J].AppliedThermalEngineering, 2015,84: 74-81. DOI:10.1016/j.applthermaleng.2015.03.019.
[4] 马美倩, 吕伟为, 沈国清, 等. 基于声学测温与最小二乘支持向量机的锅炉炉膛灰污监测方法[J]. 电力科学与工程, 2012, 28(7): 46-50,70. DOI:10.3969/j.issn.1672-0792.2012.07.009.
Ma Meiqian, Lü Weiwei, Shen Guoqing, et al. Method of furnace fouling monitoring based on acoustic pyrometry and least squares support vector machine[J].ElectricPowerScienceandEngineering, 2012,28(7): 46-50,70. DOI:10.3969/j.issn.1672-0792.2012.07.009. (in Chinese)
[5] 俞海淼, 曹欣玉, 李志, 等. 应用灰污热流计监测燃煤锅炉炉膛灰污结渣的动态过程[J]. 动力工程, 2005, 25(1): 88-91. DOI:10.3321/j.issn:1000-6761.2005.01.018.
Yu Haimiao, Cao Xinyu, Li Zhi, et al. Research on the dynamic process of ash deposition in boilers with heat flux probes[J].ChineseJournalofPowerEngineering, 2005,25(1): 88-91. DOI:10.3321/j.issn:1000-6761.2005.01.018. (in Chinese)
[6] 蒋泓亮, 安连锁, 沈国清. 基于清洁因子模型的炉膛结渣污染监测的研究[J]. 电力科学与工程, 2012, 28(9): 33-37.
Jiang Hongliang, An Liansuo, Shen Guoqing. Boiler slagging pollution monitoring research based on the model of clean factor[J].ElectricPowerScienceandEngineering, 2012,28(9): 33-37. (in Chinese)
[7] 杨祥良, 李庚生, 安连锁, 等. 基于声学测温技术的电站锅炉水冷壁灰污监测方法[J]. 华北电力大学学报, 2010, 37(3): 59-63. DOI:10.3969/j.issn.1007-2691.2010.03.011.
Yang Xiangliang, Li Gengsheng, An Liansuo, et al. A method of furnace water wall slagging monitoring in power plant based on acoustic pyrometry[J].JournalofNorthChinaElectricPowerUniversity, 2010,37(3): 59-63. DOI:10.3969/j.issn.1007-2691.2010.03.011. (in Chinese)
[8] 施永红, 云峰, 魏铁铮. 燃煤电站锅炉受热面积灰结渣在线监测的研究[J]. 电站系统工程, 2010, 26(6): 49-50, 53. DOI:10.3969/j.issn.1005-006X.2010.06.017.
Shi Yonghong, Yun Feng, Wei Tiezheng. Research on ash fouling monitoring of heating surfaces in coal-fired utility boiler[J].PowerSystemEngineering, 2010,26(6): 49-50, 53. DOI:10.3969/j.issn.1005-006X.2010.06.017. (in Chinese)
[9] 北京锅炉厂. 锅炉机组热力计算标准方法 [M].北京: 机械工业出版社, 1976: 28-38.
[10] 周强泰, 赵伶玲. 考虑辐射强度沿截面方向减弱的炉内传热公式[J]. 东南大学学报(自然科学版), 2008, 38(6): 1004-1010. DOI:10.3321/j.issn:1001-0505.2008.06.014.
Zhou Qiangtai, Zhao Lingling. Study on radiation heat transfer in boiler furnaces by taking radiant intensity attenuation in cross section into consideration[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2008,38(6): 1004-1010. DOI:10.3321/j.issn:1001-0505.2008.06.014.(in Chinese)
[11] 周强泰. 锅炉原理 [M]. 3版.北京: 中国电力出版社, 2013:161-176.
[12] 张衍国. 炉内传热原理与计算[M]. 北京: 清华大学出版社, 2008: 103-105.
[13] 阎维平, 朱予东, 谭蓬, 等. 变负荷工况下锅炉对流受热面污染的监测[J]. 动力工程, 2007, 27(1): 58-61, 129. DOI:10.3321/j.issn:1000-6761.2007.01.014.
Yan Weiping, Zhu Yudong, Tan Peng, et al. Ash fouling monitoring of boilers convective heat delivery surfaces during variable load operation[J].JournalofPowerEngineering, 2007,27(1): 58-61, 129. DOI:10.3321/j.issn:1000-6761.2007.01.014. (in Chinese)
[14] 欧宗现. 1 000 MW超超临界机组受热面污染在线监测方法研究[D]. 保定:华北电力大学能源与动力工程学院, 2009.
[15] 欧宗现, 阎维平, 朱予东. 燃煤电站锅炉的吹灰策略研究[J]. 热能动力工程, 2009, 24(3): 342-346.
Ou Zongxian, Yan Weiping, Zhu Yudong. Research on soot-blowing tactics for coal-fred utility boilers[J].JournalofEngineeringforThermalEnergyandPower, 2009,24(3): 342-346. (in Chinese)
[16] 邓喆. 基于声学测温与神经网络的炉膛污染在线监测研究[D]. 保定:华北电力大学能源与动力工程学院, 2012.
[17] 陈宝康, 阎维平, 朱予东, 等. 燃煤电站锅炉对流受热面灰污层增长预测模型的研究[J]. 华北电力大学学报, 2004,31(2): 32-35. DOI:10.3969/j.issn.1007-2691.2004.02.009.
Chen Baokang, Yan Weiping, Zhu Yudong, et al. Prediction of ash fouling on heat transfer surface of coal-fired utility boiler[J].JournalofNorthChinaElectricPowerUniversity, 2004,31(2): 32-35. DOI:10.3969/j.issn.1007-2691.2004.02.009. (in Chinese)
[18] Shi Y H, Wang J C, Liu Z F. On-line monitoring of ash fouling and soot-blowing optimization for convective heat exchanger in coal-fired power plant boiler[J].AppliedThermalEngineering, 2015,78: 39-50. DOI:10.1016/j.applthermaleng.2014.12.002.
