基于IUPF算法与可变参数电池模型的SOC估计方法

刘新天 李 贺 何 耀 郑昕昕 曾国建

(合肥工业大学智能制造技术研究院, 合肥 230009)

锂电池荷电状态(SOC)直接反映电池的剩余容量[1],并在一定程度上反映电动汽车的续航里程[2]．SOC的准确估计对实现电池电量的有效管理和续航里程的准确预估、避免电池过充和过放具有重要意义[3-4]．锂电池在使用过程中表现出较高的非线性,针对这一特性,目前常用的SOC估计算法主要有2类:① 基于卡尔曼滤波思想的方法．基于无迹变换的无迹卡尔曼滤波(UKF)算法,与扩展卡尔曼滤波(EKF)算法相比不需要对系统方程进行线性化,从而能更加真实地反映整个系统的特性,有助于系统精度的提升[5-6]．② 基于粒子滤波思想的算法[7]．相对于卡尔曼系列滤波算法，基于粒子滤波思想算法更适用于非线性系统,但该类算法固有粒子匮乏且计算量较大,在应用中实时响应性能较差．结合2类算法的优缺点,文献[8]在UKF算法的基础上，结合粒子滤波算法产生非线性粒子滤波的建议分布，实现基于无迹卡尔曼粒子滤波(UPF)算法，有较高估算精度．但当系统状态噪声和量测噪声二者所带来影响较大时,上述滤波算法的估计精度难以得到保证．

滤波算法的准确性很大程度上取决于所建立电池模型能否反应电池真实特性,因此建立较为精确的电池模型是提高SOC估算精度的关键．为保证模型的实时有效性,在实际建模过程中,应在保证模型精度的同时尽量减小电池模型复杂度．对常见Thevenin模型、RC模型、PNGV模型和Rint模型[9-11],Thevenin模型具有易进行模型参数辨识实验、物理意义明确等优点,被广泛应用于电池建模中[12]．但传统Thevenin模型中模型参数固定,无法及时反应电池的实时动态特性．针对此问题,文献[13]通过对Thevenin模型中模型参数与SOC关系的分析,在SOC的基础上建立了可变参数Thevenin模型．文献[14-16]阐述了电池的温度特性,为Thevenin模型中模型参数与温度关系的拟合提供了依据．

通过上述对SOC估计研究的分析,本文首先通过对锂电池内阻变化规律的分析,建立受温度T和SOC影响的可变参数Thevenin模型．因锂电池寿命也会导致电池参数的变化,为保证所建立模型的准确及适用性,本文选择同类型同一批次的多个电池单体作为研究对象,在实际建模过程中,暂不考虑电池寿命的影响．然后在所建立电池模型的基础上将系统状态噪声和量测噪声两者引入到UPF算法初始状态中,使采样点中含有此类噪声,进而提出一种基于IUPF算法与可变参数电池模型的SOC估计方法,并对IUPF算法的优势及其对SOC状态的估计过程进行了分析．最后通过实验和仿真验证了所采用模型的有效性和对SOC估计的优越性．

1 电池模型的建立

根据传统Thevenin模型建立受温度T和SOC影响的可变参数Thevenin模型,如图1所示．

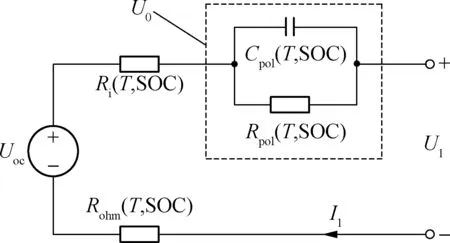
图1 可变参数Thevenin模型

根据图1模型建立如下模型参数方程:

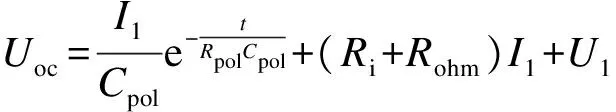
(1)

式中,Uoc,U1分别为开路电压、端电压;Rpol,Cpol分别为极化内阻、极化电容;Rohm,Ri分别为欧姆内阻和其他内阻;I1为充放电电流.Cpol,Rpol,Rohm和Ri均为受SOC和温度T影响的可变参数,为对模型参数进行较好的拟合,选取单节额定容量为9 A·h的锂电池,通过混合动力脉冲特性(HPPC)实验[17],对模型中Rohm,Rpol等参数进行测定．其中，U0为极化电压.

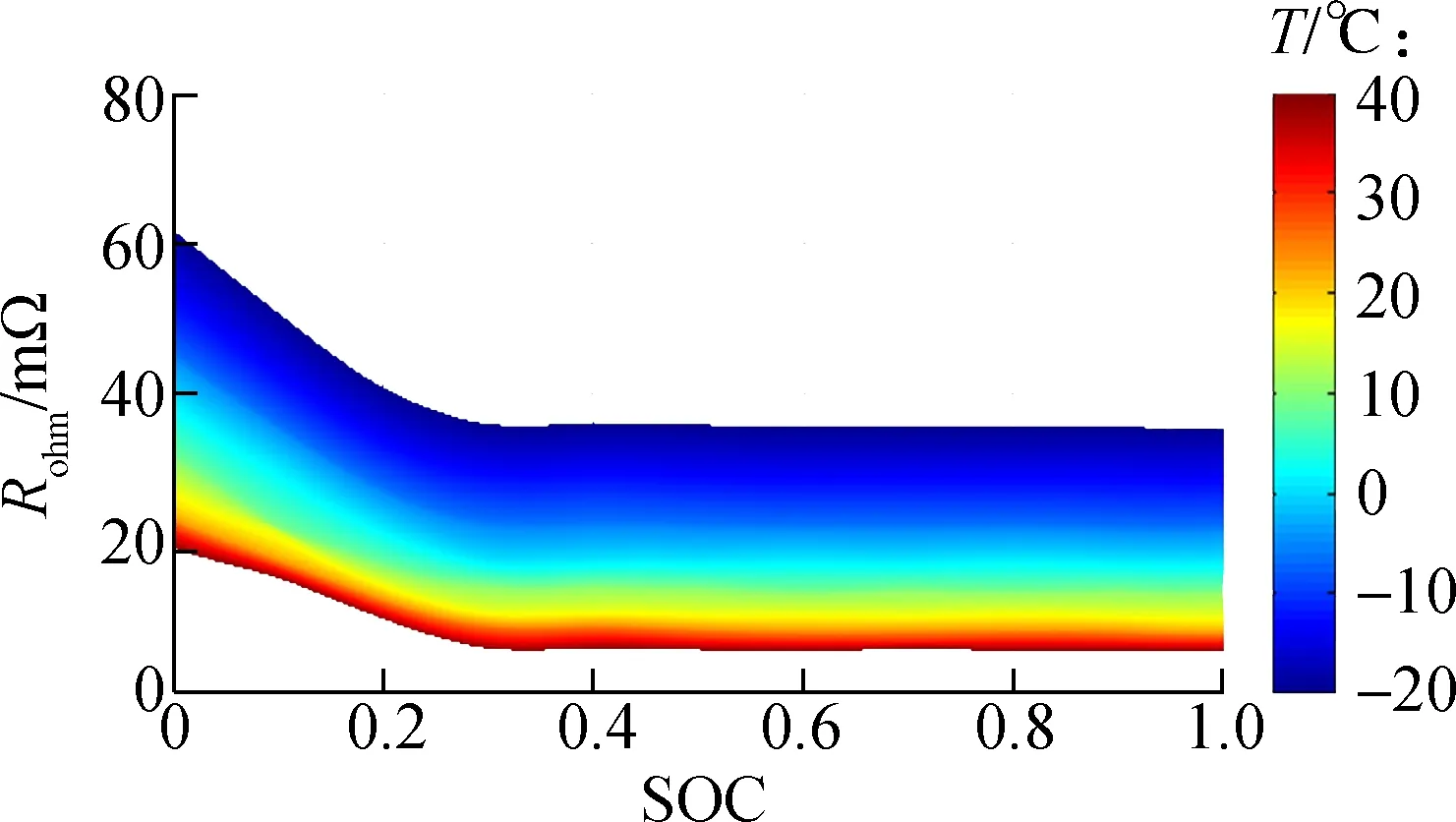
图2给出了通过多次HPPC实验测得的Rohm与SOC,T的关系．通过对图2分析可知:在SOC<0.3时Rohm随温度T和SOC两者同时变化;在SOC>0.3时Rohm只随温度T变化,且在SOC<0.6时Rohm的阻值比SOC>0.6时的阻值略高．为提高模型准确性将SOC分为[0,0.3)、[0.3,0.6)、[0.6,1]三个区域对Rohm进行分析．

图2 测定Rohm与SOC，T的关系

与上述类似,可通过HPPC实验测得Rpol和SOC,T的关系,如图3所示．

图3 测定的Rpol和SOC，T关系

通过对图3的分析可知,Rpol与Rohm具有类似的变化规律,因此也将SOC分为[0,0.3)、[0.3,0.6)、[0.6,1]三个区域来对Rpol进行分析．

2 电池模型参数的辨识

为得到实际各参数与SOC,T的函数关系,利用离散数据拟合的方法对测量得到的不同SOC下各温度点对应的阻值进行拟合．

2.1 Rohm和Rpol的参数辨识

通过上述分析可知,在SOC<0.3时，Rohm,Rpol随T和SOC同时变化,为建立较为精确的电池模型同时又使电池模型不过于复杂,在SOC<0.3时,将SOC和T作为等效内阻模型输入量,采用两水平因子实验设计(DOE)方法进行拟合．中心复合设计(CCD)具有设计简便、系统性强等优势,在DOE应用中最为常见．本文将基于CCD的DOE应用于内阻模型中,把T,SOC作为输入量对内阻进行拟合,拟合的等效内阻模型包含一次项、二次项和交叉项,拟合原理如图4所示．

图4 基于CCD的内阻DOE模型

当SOC>0.3时温度T是影响内阻变化的主要因素,可将温度T作为输入量利用最小二乘法对内阻进行拟合．

通过以上分析,对Rohm,Rpol进行分段拟合,结果如图5所示．

(a) 测定Rohm与SOC的关系

(b) 拟合Rohm与SOC的关系

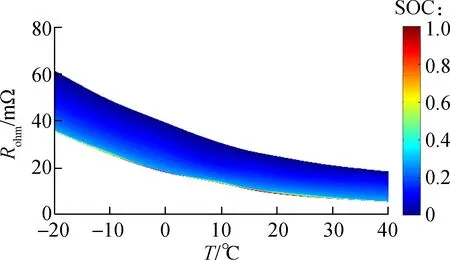
(c) 测定Rohm与温度T的关系

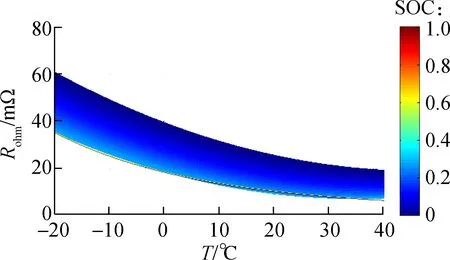
(d) 拟合Rohm与温度T的关系

图5中给出了测定及拟合Rohm与SOC，T的关系,其对应的分段拟合方程为

(2)

式中,a0,a1,…,a5,b0,b1,b2,c0,c1,c2为系数.

表1是同类型同一批次多个电池单体进行多次拟合的均值,在实际应用时应有95%置信度水平的置信区间.因为在实际应用中会有大量的电池,同种电池单体参数基本上都存在差异,分段拟合所得的Rohm与SOC,T关系图如图6所示．

表1 Rohm参数辨识

由上述HPPC实验可知,测得的Rpol与Rohm具有相似的性质,因此本文对Rpol采用类似分段拟合方法进行拟合．对于其他内阻Ri,由于相对于Rohm和Rpol较小,因此在电池建模中将其忽略不计．

2.2 Cpol参数的辨识

电池停止放电3τ时间后,极化电压将衰减95%,通过充放电实验得到典型温度下电池极化过程时间常数τ的测量结果，如表2所示．

表2 典型温度下τ的测量值

通过对测量数据分析，得到如下参数τ的拟合方程:

τ=k1eTk2+k3

(3)

式中,k1,k2,k3为辨识参数,如表3所示．

表3 τ参数辨识

由此可得Cpol表达式为

(4)

3 算法模型

为了表征温度、充放电倍率、容量等对SOC估计的影响,电池SOC状态方程可表示为

(5)

κ=|i(t)|/CN

(6)

式中,SOC(0),SOC(t)分别为0,t时刻的SOC值;η为充放电效率,根据锂电池充放电特性,在不同温度及SOC下锂电池的充放电效率都近似为1[18],因此为了在保证电池模型精度的同时又使模型不至于特别复杂,此处充放电效率取为1;i(τ) 为充放电电流;κ为充放电倍率;CN为常温下电池的标称容量;C(T,κ,t)为电池在不同充放电倍率及温度条件下的可用容量．

根据图1及式(1),建立如下参数方程:

U1(T,SOC)=Uoc-Rohm(T,SOC)I1-U0(T,SOC)

(7)

将式(5)、(7)离散化,可得到如下离散状态空间方程:

(8)

yk+1=h(xk,uk)+wk=

Uoc-Rohm(T,xk)uk-U0(T,xk)+wk

(9)

式中,xk,Δt分别为第k次计算得到的SOC值和采样周期;vk,wk分别为系统状态噪声和量测噪声,两者皆是均值为零、方阵分别为Q和R的不相关的高斯白噪声；yk为观测变量,表征利用电池模型进行第k次计算得到的端电压U1;uk为输入变量,表征第k次计算时电池充放电电流I1．

当系统状态噪声和量测噪声影响较大时,传统滤波算法很难保证其估计精度．针对此问题,本文将系统状态噪声和量测噪声引入到UPF算法初始状态中,使采样点中含有此类噪声．从而在状态预测和更新过程中,系统噪声的影响能够在非线性系统中传输和估计,使滤波信号更好地趋近于真实值,实现基于IUPF算法的SOC估计．根据所建立电池模型的状态空间方程,利用IUPF算法实现SOC状态估计过程.

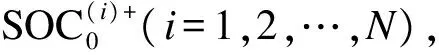
(10)

(11)

(12)

(13)

然后,当k=1,2,…时,IUPF算法的状态具体估算过程如下.

① 粒子Sigma点采样为

(14)

其中状态变量为

(15)

(16)

状态方差为

(17)

② 粒子和估计误差协方差时间更新过程为

(18)

(19)

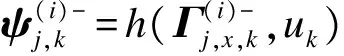
(20)

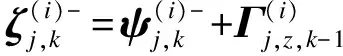
(21)

(22)

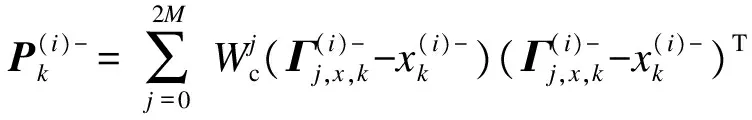
(23)

③ 粒子量测更新过程为

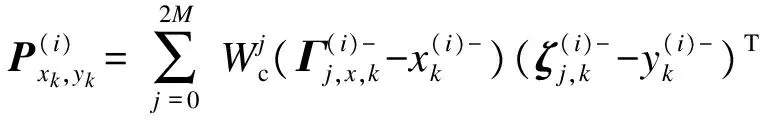
(24)

(25)

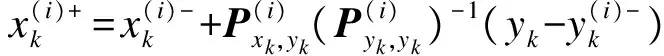
(26)

(27)

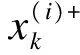
(28)

进行归一化后得到

(29)

3) 更新SOC值,得到

(30)

上述IUPF算法采用多粒子改进的UKF算法,在一定程度上去除了使用单粒子卡尔曼滤波时由于系统非线性及因噪声的非高斯分布而产生的系统误差以及可能存在的发散性;同时将系统状态噪声和量测噪声引入到采样点中,在状态预测和更新过程中,系统噪声的影响就可以在非线性系统中传输和估计．在时间更新、量测更新过程中,状态值考虑过程噪声的影响,测量值考虑量测噪声的影响,使得滤波信号更好地趋近真实值,提高了SOC估计的精度．

4 仿真和实验验证

4.1 电池模型精度的验证

为了对可变参数Thevenin模型的精度进行验证,选取单节额定容量为9 A·h的磷酸铁锂电池分别在-20,-10,0,10,20 ℃环境下进行充放电实验．实验测试平台原理图如图7所示．

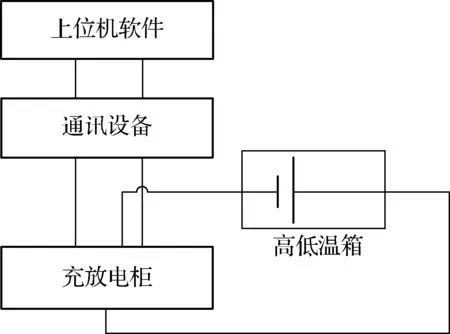
图7 实验测试平台原理图

图7中,高低温箱为Partner高低温箱;充放电柜为恒翼能充放电柜(HT10080C);通讯设备为恒翼能RS-485/232转换器;上位机软件为HYN HighPower Battery Test System;充放电在对电池模型进行参数辨识时,采用了HPPC工况,为充分验证电池模型具有较高的精度,此处放电波形采用USABC实验手册中规定的DST工况波形．经过每个DST工况,电池放出0.45 A·h的电量,20 ℃时20次循环可将电池电量放完．将各温度下可变参数Thevenin模型端电压与实测端电压以及传统Thevenin模型端电压进行比较．

图8给出了多个温度下进行DST工况充放电实验时锂电池端电压变化曲线．通过对图8及多个温度下进行DST工况充放电实验时锂电池的端电压的分析可得:常温下可变参数Thevevnin模型和传统Thevenin模型参数相差不大;而低温环境下模型参数受温度影响较大,故传统Thevenin模型估计精度较差．表4给出了各温度下2种模型端电压的平均绝对误差,其表达式为

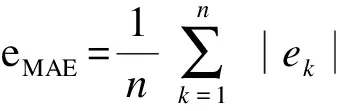
(31)

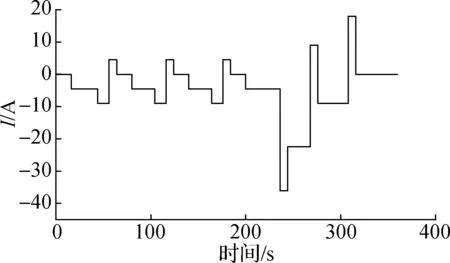
(a) DST工况电流曲线

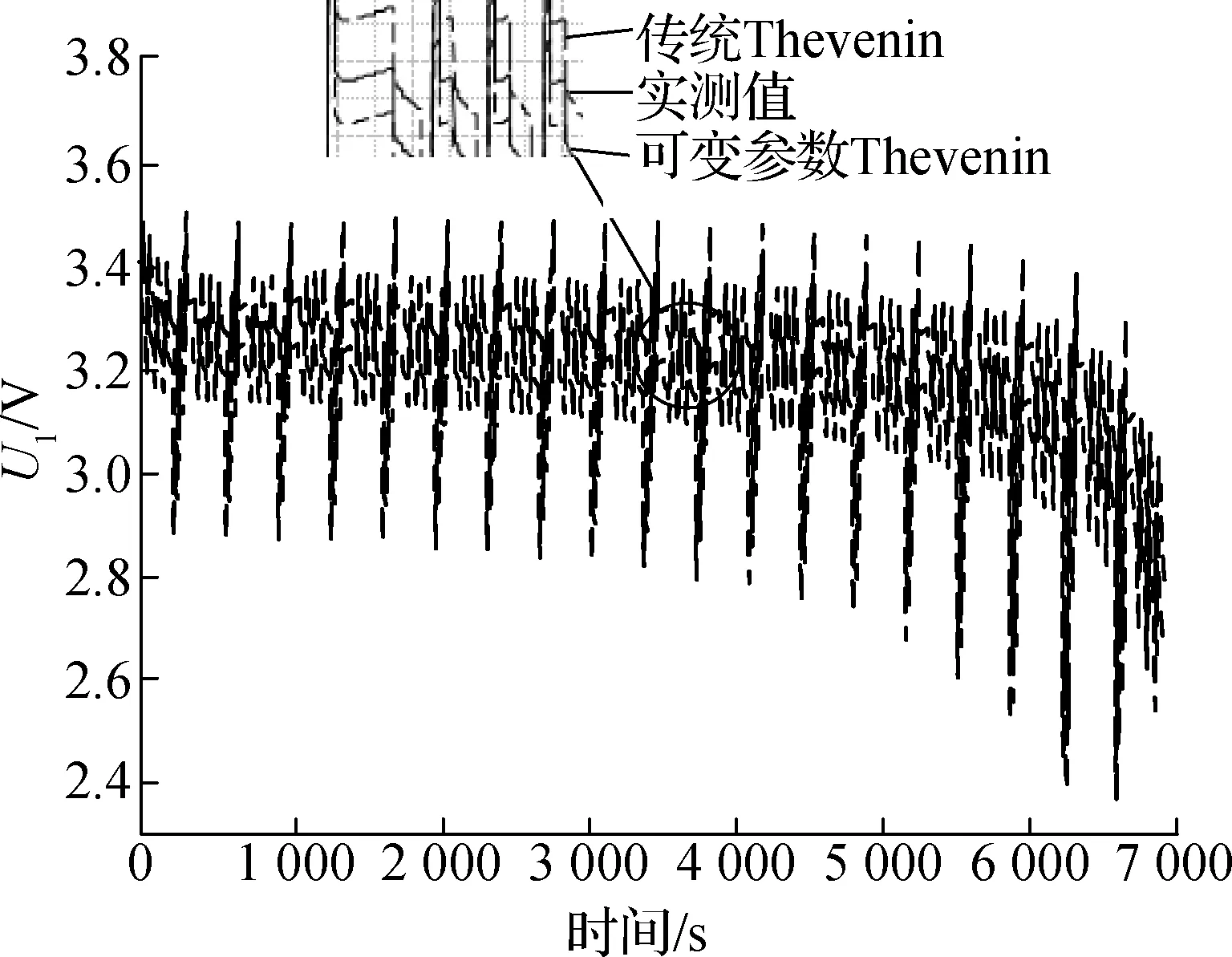
(b) 20 ℃两种电池模型端电压

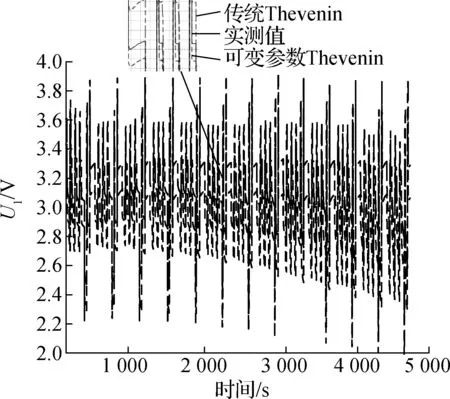
(c) -10 ℃两种模型的端电压

式中,eMAE,ek分别为平均绝对误差和k时刻绝对误差．通过对图8及在多个温度下DST工况充放电实验电池的端电压变化分析，以及结合表4可以看出,通过HPPC实验方法建立的电池模型在DST工况下仍具有精度高、误差小的特点,充分验证了所建立电池模型的准确性．

表4 端电压平均绝对误差 V

4.2 SOC估计精度的验证

为了验证IUPF算法对锂电池SOC估计的优越性,选取单节额定容量为9 A·h的磷酸铁锂电池,以3 A电流脉冲放电,放电电流波形见图9．进行MATLAB仿真实验,将IUPF与EKF,UKF,UPF从估算误差、鲁棒性等方面进行比较．初始时保持电池为满电状态(即SOC=100%),仿真时将粒子数设为50,将(0,1)均匀分布产生的50个粒子的估计方差初值设为1．在具体仿真过程中,依照IUPF算法状态估计过程进行SOC值的不断计算更新,得到SOC估计曲线．为了定量比较各算法的性能,在不同工况下对各算法的最大估计误差进行分析．

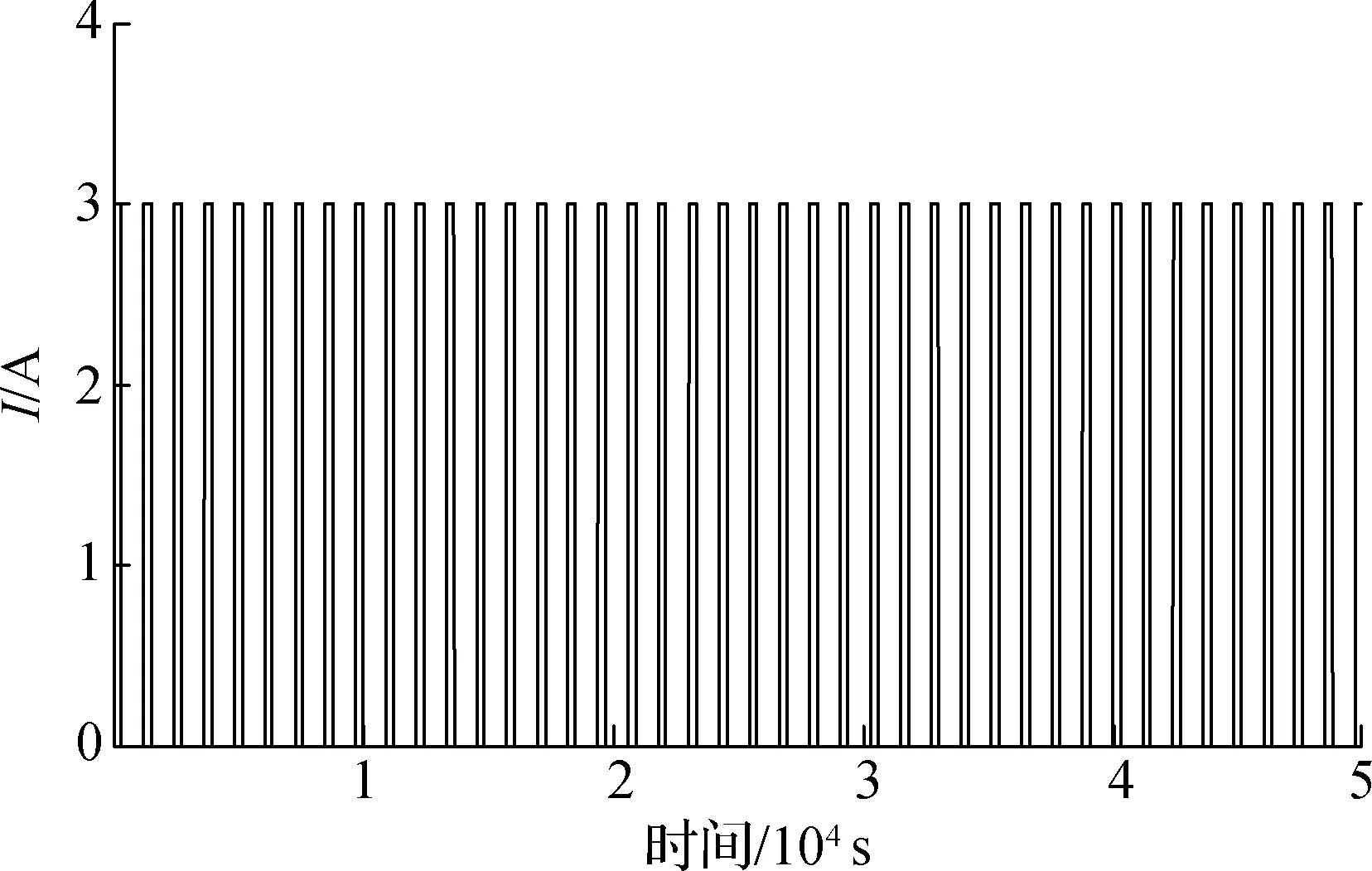
图9 放电电流曲线

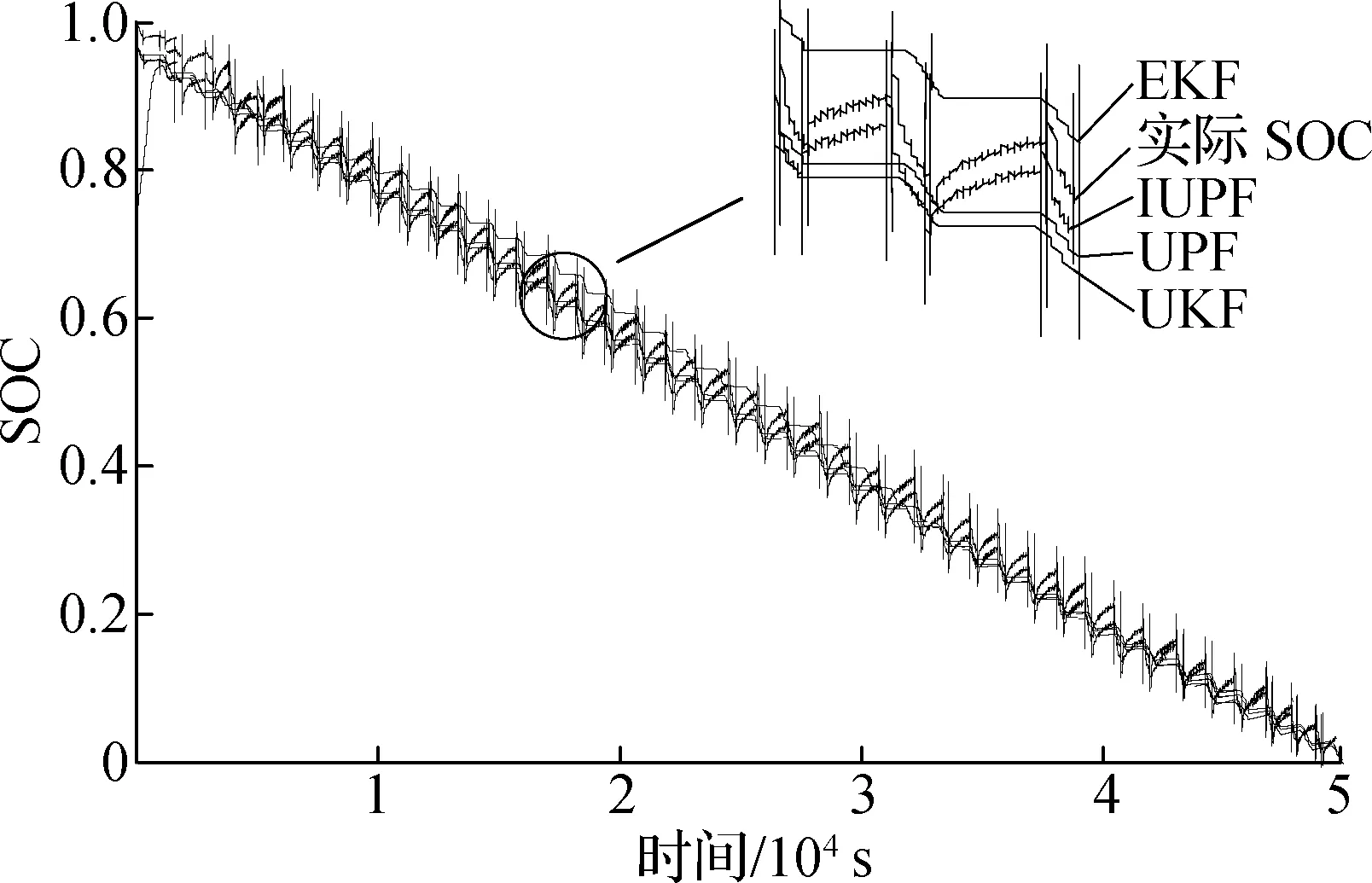
1) 在常温(20±1) ℃下对IUPF算法在系统状态、量测噪声影响较大时的估算精度进行验证,分别进行以下仿真实验:初始给予系统较小的系统噪声、量测噪声,得到各类算法SOC估计及误差曲线．通过对图10的分析和结合表5中各算法的最大估算误差可以发现,UPF和IUPF算法估算精度可达到2.1%左右,相对于常用的EKF算法精度提高了约1.6%．然后取量测噪声wk～(0,0.1)、状态噪声vk～(0,0.1),得到IUPF,UPF,UKF等算法SOC估计及误差曲线见图11．通过对比图11误差曲线和结合表6可以发现,在系统量测噪声和状态噪声影响较大时相对于常用算法，IUPF算法估算精度明显提高．

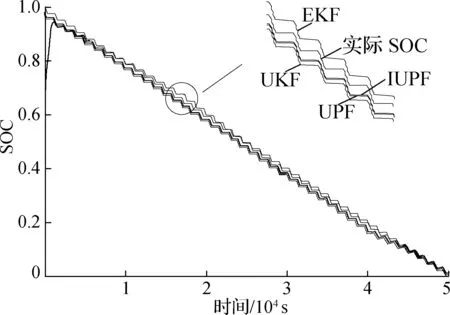
(a) SOC估计曲线

(b) SOC估计误差曲线

算法EKFUKFUPFIUPF最大估计误差/%3．632．362．112．02

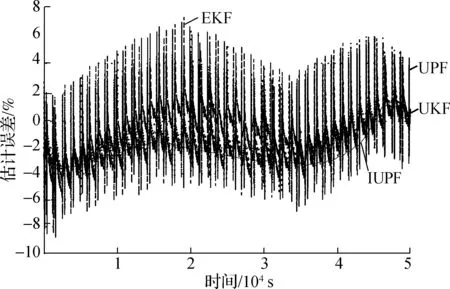
(b) SOC估计误差曲线

算法EKFUKFUPFIUPF最大估计误差/%9．136．866．513．32

2) 为验证系统在低温下仍具有较高的估算精度,在低温(-10±1) ℃下进行3 A电流脉冲的放电实验,得到不同算法估计及误差曲线见图12．通过对图12的分析和结合表7中各算法的最大估算误差可以发现, 在低温条件下,所采用的基于IUPF算法与可变参数电池模型的SOC估计方法仍具有良好的估算精度．

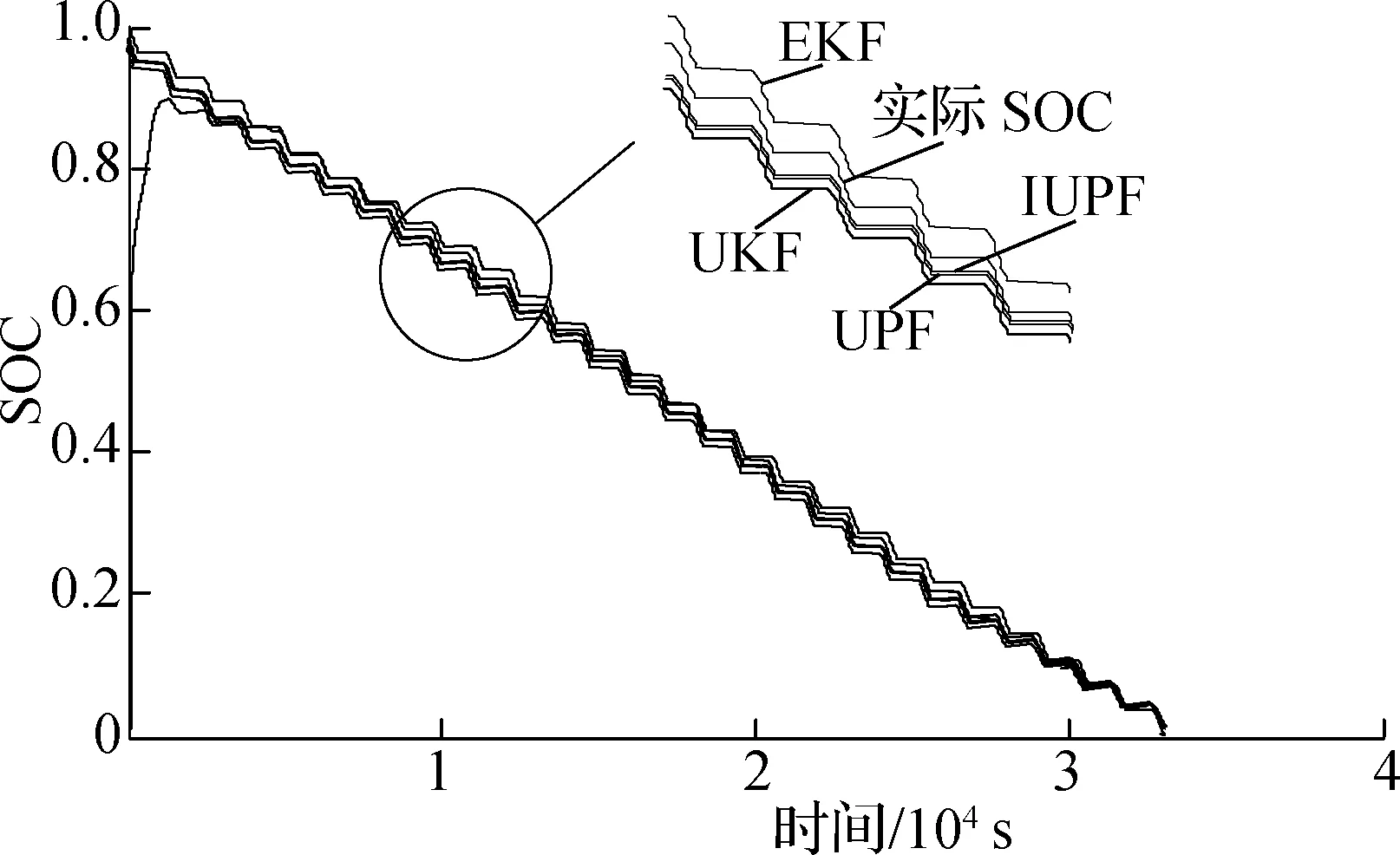
(a) SOC估计曲线

(b) SOC估计误差曲线

算法EKFUKFUPFIUPF最大估计误差/%5．743．583．243．19

3) 为验证所建立的IUPF算法在模型参数扰动时的鲁棒性,在3 A脉冲电流放电条件下,给予开路电压U0一定的扰动,得到各算法SOC估计及误差曲线见图13．通过对图13分析和结合表8中各算法最大估算误差可以发现,IUPF算法与UPF算法类似,相对于其他算法,对由模型参数扰动带来的干扰有较强鲁棒性．

通过对上述仿真实验中各个状态下各算法估计曲线及误差曲线的分析,可以发现IUPF算法在多个温度下相对于其他常用算法具有较高的估算精度．尤其是在系统状态噪声、量测噪声影响较大时,IUPF算法相对于精度较高的UPF算法估算精度提高了约3.2%,且对模型参数所带来的扰动具有良好的抗干扰性能．

(a) SOC估计曲线

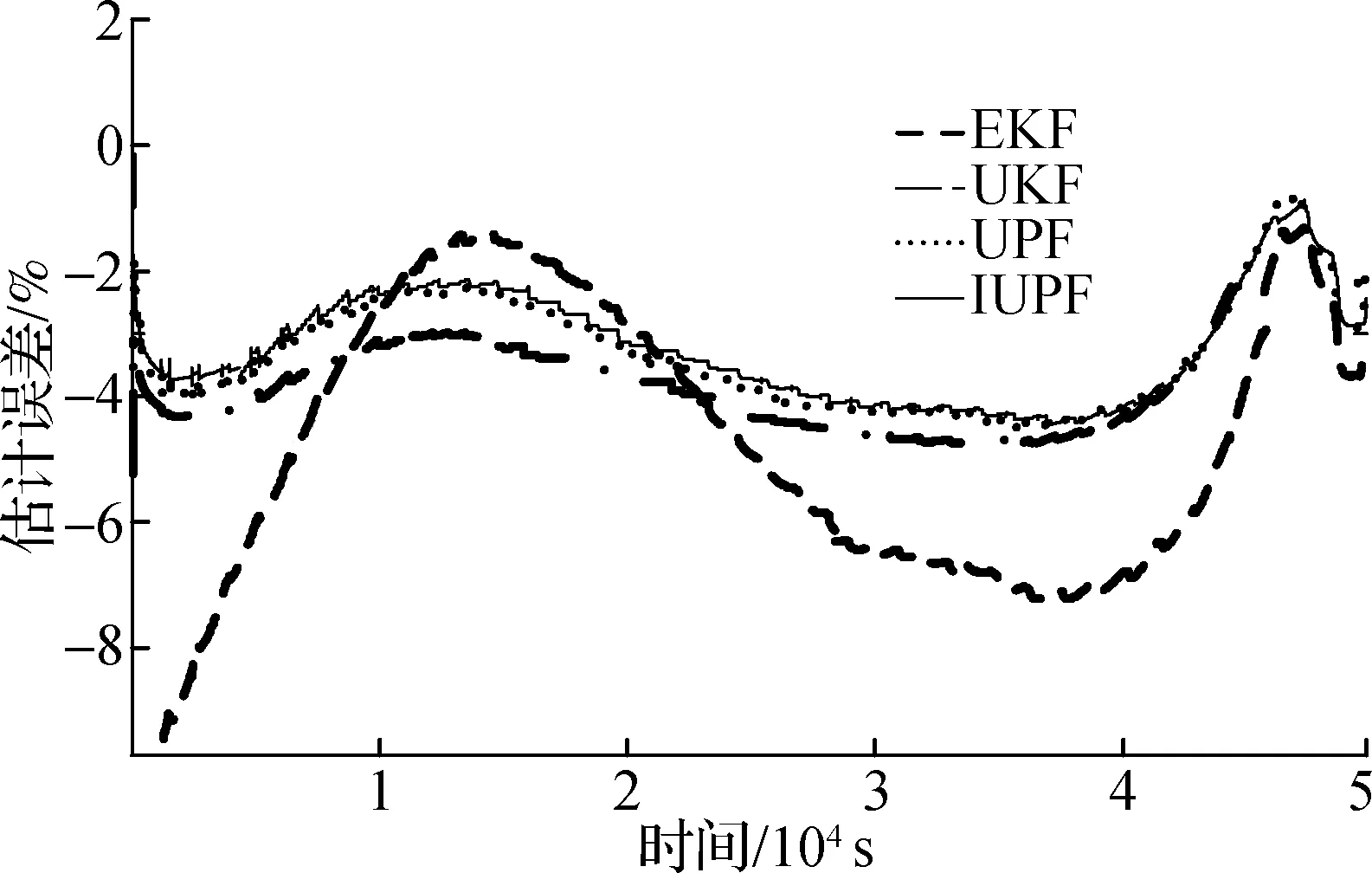
(b) SOC估计误差曲线

算法EKFUKFUPFIUPF最大估计误差/%6．924．854．284．21

5 结论

1) 根据锂电池内阻变化规律及同种电池单体存在差异的特点,在95%置信水平上利用基于CCD的DOE和最小二乘法等参数拟合方法对电池模型参数进行辨识．所建立的模型参数受温度T和SOC影响的可变参数的Thevenin模型解决了现有模型适用范围有限的问题,保证了电池模型的精度及适用性;所采用的参数拟合方法能够根据较少测量数据得到较为精确的电池模型,在保证模型精度的同时减少了工作量．

2) 通过对系统噪声和量测噪声影响较大时对滤波算法估计精度所带来影响的分析,提出了IUPF算法将系统状态噪声和量测噪声两者同时引入到采样点当中,在状态预测和更新过程中,系统噪声的影响就可以在非线性系统中传输和估计．与其他常用算法相比,所提出的IUPF算法,在较大的温度范围内具有较高的估算精度,尤其是在状态噪声、量测噪声影响较大时,其估计精度有明显的提高．

)

[1] Chaoui H, Gualous H. Adaptive state of charge estimation of lithium-ion batteries with parameter and thermal uncertainties [J].IEEETransactionsonControlSystemsTechnology, 2017,25(2): 752-759. DOI: 10.1109/TCST.2016.2572362．

[2] 刘毅, 谭国俊, 何晓群. 优化电池模型的自适应Sigma卡尔曼荷电状态估算[J]. 电工技术学报, 2017, 32(2): 108-118. DOI:10.19595/j.cnki.1000-6753.tces.2017.02.013.

Liu Yi, Tan Guojun, He Xiaoqun. Optimized battery model based adaptive sigma Kalman filter for state of charge estimation [J].TransactionsofChinaElectrotechnicalSociety, 2017,32(2): 108-118. DOI:10.19595/j.cnki.1000-6753.tces.2017.02.013. (in Chinese).

[3] Chen J, Xu C F, Su H Y, et al. Neural network-based state of charge observer design for lithium-ion batteries [J].IEEETransactionsonControlSystemsTechnology, 2018,26(1): 313-320. DOI: 10.1109/TCST.2017.2664726.

[4] 吴铁洲, 罗蒙, 张琪, 等. 基于迭代扩展卡尔曼滤波算法的电池SOC估算[J]. 电力电子技术, 2016, 50(5): 95-98. DOI:10.3969/j.issn.1000-100X.2016.05.028

Wu Tiezhou, Luo Meng, Zhang Qi, et al. Battery SOC estimation based on iterative extended Kalman filter algorithm [J].PowerElectronics, 2016,50(5): 95-98.DOI:10.3969/j.issn.1000-100X.2016.05.028. (in Chinese)

[5] 何耀, 张陈斌, 刘兴涛, 等. 基于信息融合的LiFePO4动力电池组SOC估计[J]. 控制与决策, 2014, 29(1):188-192. DOI:10.13195/j.kzyjc.2012.1441.

He Yao, Zhang Chenbin, Liu Xingtao, et al. SOC estimation for LiFePO4high-power batteries based on information fusion [J].ControlandDecision, 2014,29(1):188-192. DOI:10.13195/j.kzyjc.2012.1441. (in Chinese)

[6] 刘江, 王玉金, 段建雷, 等. 基于高斯分布的多层无迹卡尔曼滤波算法[J]. 控制与决策, 2016, 31(4): 609-615. DOI:10.13195/j.kzyjc.2015.0039.

Liu Jiang, Wang Yujin, Duan Jianlei, et al. Multi-layer unscented Kalman filtering algorithm based on Gaussian distribution[J].ControlandDecision, 2016,31(4):609-615. DOI:10.13195/j.kzyjc.2015.0039. (in Chinese)

[7] 汪永志, 贝绍轶, 汪伟, 等. 基于粒子滤波算法的动力电池SOC估计[J]. 机械设计与制造工程, 2014, 43(10):69-73. DOI:10.3969/j.issn.2095-509X.2014.10.016.

Wang Yongzhi, Bei Shaoyi, Wang Wei, et al. Battery state of charge estimation based on particle filter algorithm[J].MachineDesignandManufacturingEngineering, 2014,43(10): 69-73. DOI:10.3969/j.issn.2095-509X.2014.10.016． (in Chinese)

[8] 何耀. 动力锂电池组状态估计策略及管理系统技术研究[D]. 合肥:中国科学技术大学自动化系, 2012.

[9] 陈息坤, 孙冬, 陈小虎. 锂离子电池建模及其荷电状态鲁棒估计 [J]. 电工技术学报, 2015, 30(15): 141-147. DOI:10.19595/j.cnki.1000-6753.tces.2015.15.016.

Chen Xiqun, Sun Dong, Chen Xiaohu. Modeling and state of charge robust estimation for lithium-batteries [J].TransactionsofChinaElectrotechnicalSociety, 2015,30(15): 141-147. DOI: 10.19595/j.cnki.1000-6753.tces.2015.15.016. (in Chinese)

[10] 戴海峰, 魏学哲, 孙泽昌. 基于等效电路的内阻自适应锂离子电池模型[J]. 同济大学学报(自然科学版), 2010, 38(1): 98-102. DOI:10.3969/j.issn.0253-374x.2010.01.018.

Dai Haifeng, Wei Xuezhe, Sun Zechang. An inner resistance adaptive model based on equivalent circuit of lithium-ion batteries [J].JournalofTongjiUniversity(NaturalScience), 2010,38(1): 98-102. DOI:10.3969/j.issn.0253-374x.2010.01.018. (in Chinese)

[11] 杨世春, 麻翠娟. 基于PNGV改进模型的SOC估计算法[J]. 汽车工程, 2015, 37(5): 582-586,598. DOI:10.19562/j.chinasae.qcgc.2015.05.018.

Yang Shichun, Ma Cuijuan. SOC estimation algorithm based on improved PNGV model [J].AutomotiveEngineering, 2015,37(5): 582-586,598. DOI:10.19562/j.chinasae.qcgc.2015.05.018. (in Chinese)

[12] Xiong R, He H W, Zhao K. Research on an online identification algorithm for a thevenin battery model by an experimental approach [J].InternationalJournalofGreenEnergy, 2015,12(3): 272-278. DOI:10.1080/15435075.2014.891512.

[13] 张阳, 潘文霞. 带可变参数锂离子电池Thevenin模型[J]. 电源技术, 2013, 37(5):755-757. DOI:10.3969/j.issn.1002-087X.2013.05.015.

Zhang Yang, Pan Wenxia. Thevenin model of lithium-ion battery with variable parameters [J].ChineseJournalofPowerSources, 2013,37(5): 755-757. DOI:10.3969/j.issn.1002-087X.2013.05.015. (in Chinese)

[14] 李哲, 韩雪冰, 卢兰光, 等. 动力型磷酸铁锂电池的温度特性[J]. 机械工程学报, 2011, 47(18): 115-120. DOI:10.3901/JME.2011.18.115.

Li Zhe, Han Xuebing, Lu Languang, et al. Temperature characteristics of power LiFePO4batteries [J].JournalofMechanicalEngineering, 2011,47(18): 115-120. DOI:10.3901/JME.2011.18.115. (in Chinese)

[15] Low W Y, Abdul Aziz M J, Idris N R N. Modeling of lithium-titanate battery with ambient temperature effect for charger design [J].IETPowerElectronics, 2016,9(6): 1204-1212. DOI:10.1049/iet-pel.2015.0639.

[16] 刘新天, 何耀, 曾国建, 等. 考虑温度影响的锂电池功率状态估计[J]. 电工技术学报, 2016, 31(13):155-163. DOI:10.19595/j.cnki.1000-6753.tces.2016.13.018.

Liu Xintian, He Yao, Zeng Guojian, et al. State-of-power estimation for li-ion battery considering the effect of temperature[J].TransactionsofChinaElectrotechnicalSociety, 2016,31(13):155-163. DOI: 10.19595/j.cnki.1000-6753.tces.2016.13.018. (in Chinese)

[17] Weizhong W, Pawel M, Khalid K, et al. Modeling, parameterization, and benchmarking of a lithium-ion electric bicycle battery [C]//IEEEEnergyConversionCongressandExposition(ECCE). Milwaukee, WI, USA, 2016:1-7. DOI:10.1109/ECCE.2016.7855266.

[18] Xingtao L, Zonghai C, Chenbin Z, et al. A novel temperature-compensated model for power Li-ion batteries with dual-particle-filter state of charge estimation [J].AppliedEnergy, 2014,123: 263-272. DOI:10.1016/j.apenergy.2014.02.072.

[19] 黄铫, 张天骐, 高清山, 等. 一种提高无迹卡尔曼滤波精确度的方法[J]. 计算机仿真, 2010, 27(3):348-352. DOI:10.3969/j.issn.1006-9348.2010.03.085.

Huang Yao, Zhang Tianqi, Gao Qingshan, et al. A method improving the accuracy of UKF [J].ComputerSimulation, 2010,27(3):348-352. DOI:10.3969/j.issn.1006-9348.2010.03.085. (in Chinese)