飞机圆周盘旋时拖缆的动力学建模与分析
2018-02-08朱延娟
朱延娟, 罗 丹
(同济大学 航空航天与力学学院,上海 200092)
航空拖曳系统主要是由飞机、拖缆和拖体三者组成的多体约束系统,其中拖缆是飞机与拖体之间的唯一连接介质,主要起能量传递和电信号传输的作用[1].航空拖曳系统有着许多实际的工程应用,如防空武器系统鉴定、军事作战目标模拟和通信系统等领域.飞机通信应用是目前各国重点研究的关键技术问题,拖缆的稳态构型和垂直度等是检验系统是否正常有效工作的重要性能指标,是设计中必须重点研究的主要问题.垂直度是拖缆在铅垂线上的投影长度与总长度之比,为确保系统能够正常有效工作,垂直度需不小于70%.若要保证垂直度在要求范围内,飞机必须在特定状态下进行稳定盘旋飞行[2].
1958年,Caughey[3]分析了拖索系统在真空中的运动,提出了动态稳定性的近似求解方法,但忽略了空气阻尼对拖索系统的影响.Lemon和Fraser[4]考虑空气阻力的情况,假设拖索是不可伸长的,发现在低阻尼和高旋转速度下拖索系统会存在不稳定性.Skop和Choo[5]把末端连接物体假设为球体,研究柔性不可伸长拖索的平衡条件与构型,该研究仅考虑了法向空气阻力.Huang[6]在圆柱坐标系下,根据牛顿第二定律推导拖索的动力学方程,确定了平衡状态的拖索构型,此方法对初始条件有着较高的要求.Zhu和Rahn[7]建立了拖索系统的动力学模型,分析系统的动态响应与稳定性,得出在小阻尼、大质量末端连接物和高旋转速度下存在稳态多解.郑小洪等[8]应用牛顿定律建立了机载甚低频拖曳天线的动力学模型,运用Newton-Raphson迭代法求解天线稳定垂直构型,分析了空气系数和末端质量对天线稳定构型的影响.此外,Choo和Casarella[9]对拖索动态仿真方法进行比较分析,认为有限元是较为通用的动态仿真法.Russell和Anderson[10]运用有限元建立了拖索系统模型,把末端物体简化为质点,定性研究了拖索系统的稳态平衡.James和Louis[11]在航空拖索上建立局部坐标系,应用有限元将拖缆离散成数分段,针对任一拖缆段建立平衡方程,运用中心差分法对其进行求解与分析.Paul和Pavel[12]应用有限元对拖索进行了建模研究,把刚性段作为无质量的二力杆,段与段之间用球铰连接,每段拖索的质量和受力都集中在节点上.拖索离散模型的研究能够有效地处理强非线性问题,并在一定程度上反映拖索的实际工作情况.目前研究拖索的相关文献较多局限于分析拖索的受力情况与方程求解.
在上述研究基础上,针对飞机的圆周盘旋运动,采用多刚体法建立了拖缆离散模型.通过对拖缆模型的数学分析,构建了一种便于仿真计算的拖缆多刚体动力学模型.并对拖缆连续模型应用微元法进行理论验证分析,结果表明所建的多刚体动力学模型是正确可信的.
1 拖缆的动力学建模
1.1 相关坐标系
对拖缆模型进行力学分析,需构建空间坐标系.空间坐标系由惯性坐标系OXYZ和旋转坐标系Oxyz构成,两者具有相同原点,旋转坐标系绕纵轴以飞机旋转角速度旋转.将拖缆离散为任意n段,运用有限元中的刚体法建立拖缆的多刚体模型.任意段拖缆有着独立的旋转坐标系R(x,y,z)和描述旋转位置方向的欧拉角γ(ψ,θ,φ).设旋转坐标系和欧拉角作为广义坐标,即:
qi=[xi,yi,zi,ψi,θi,φi]T,i=1,2,…,n
1.2 受力分析

式中:E为杨氏模量;A0为无应力作用下拖缆的横截面积;Lsj、lj分别为第j段拖缆的无应力长度和应力长度.
重力方程:
Gj=-mjgK
式中:mj为第j段拖缆质量;g为重力加速度;K为沿OZ轴方向的单位矢量.


图1 拖缆段的受力示意图

式中:CDj、CLj分别为第j段拖缆的空气阻力系数、升力系数;ρj为空气密度;dj为拖缆段直径;vj为拖缆与空气的相对运动速度;eDj、eLj分别为空气阻力和升力方向的单位矢量.
由于拖缆做三维旋转运动时阻力方向不断改变,在动力学仿真计算中较难对其进行准确的设置与计算.因此,在拖缆段旋转坐标系上将总空气阻力分解为沿惯性坐标系X、Y、Z轴方向的阻力分量,如图2所示.
拖缆力学模型的合理构建,能快速、准确地求解出运动状态.在三维流场中,第j段拖缆的空气阻力分量Fxj、Fyj、Fzj的方程式[14]如下:
式中:Vxj、Vyj、Vzj分别为第j段拖缆沿惯性坐标系x、y、z方向的流场速度;π为圆周率;cf、cp分别为空气摩擦系数和压力系数.

图2 拖缆段的力学模型
1.3 运动方程
拖缆的运动规律由运动方程求解得出.拖缆系统模型的自由度为3n(n为拖缆的段数),变量为广义坐标,则拖缆的拉格朗日运动方程为

第j段拖缆的惯性位置:
式中:C(ψj,θj,φj)为坐标转换矩阵;Xj、Yj、Zj分别为第j段拖缆的惯性坐标位移;Lsj为第i段拖缆的无应力长度.
总动能T是所有拖缆段动能的总和,则:
式中:mj,Vj分别为第j段拖缆的质量和速度.
i=1,2,…,3n
式中:FXj、FYj、FZj是第j段拖缆的惯性作用力.
2 拖缆运动的理论验证分析
多刚体法建立拖缆离散模型,可以省去拖缆段间约束力的繁琐计算,动力学模型的合理构建,能够快速准确获得拖缆的运动状态.由于拖缆连续模型更接近于实际形状,因此对拖缆连续模型应用微元法进行理论分析,并与拖缆离散系统的稳态构型结果进行对比.
2.1 连续模型的构建
采用有限元法是把拖缆离散化成一系列的拖缆段模型,而微元法是在拖缆任意一点上取细小微元进行分析.设拖缆自然无伸展状态、稳定状态和动态平衡状态下任意位置E的弧坐标分别为S0、S1、S2.任意E点的位移表示为
U(S0,T)=R2(S0,T)-R1(S0)
(1)
式中:U(S0,T)为E点从稳定状态到动态平衡T时刻的位移;R2(S0,T)为动态平衡中O点到E点在T时刻的距离;R1(S0)为稳定状态中O点到E点的距离.
在拖缆任意E点取微元,对其进行受力分析如图3所示,根据牛顿定律可得拖缆的运动方程:
(2)
式中:P为拖缆所受的张力;Fw为拖缆重力;FI为拖缆的惯性力;FD为法向空气阻力.
我们为什么会主张社会主义市场经济?这不仅是我们观察世界的结果,也是回归本民族历史的思考。经济学理论告诉我们,好的制度应该是“内生”的,中国在社会主义市场经济体制下表现良好,是因为这种制度选择符合我们自己的历史。按照市场经济等于资本主义的标准,很多人不认为中国古代是市场经济国家,我们在此且不论这种看法的偏颇性,我们仅仅强调,市场经济存在于古代中国,且为古代中国的发展做出了巨大贡献。我们认为,市场经济作为一种自发秩序,在中国和欧洲都有遥远的历史。只要人们生产有了剩余需要交换,市场和贸易就会自然而然产生。当然古代的市场规模与所包含的内容与现代社会是不能比拟的,但从促进资源配置的功能看却是一致的。

图3 拖缆微元受力示意图
由于拖缆的切向阻力部分很小,可以忽略不计,因此FD只考虑法向空气阻力[8].则:
(3)
式中:P为拖缆张力的数值大小;ρ1为拖缆单位长度密度;ρ2为空气密度;aE为任意E点的加速度;Dn为法向空气阻力系数;Vn为拖缆相对于空气的法向速度;A0为无应力作用下拖缆的横截面积;k为Oz轴的单位矢量.
拖缆末端连接着拖体,由于拖体的作用,因此存在固有边界条件:
P+FDw+FDI+FDH=0
(4)
其中,拖体的重力FDw、惯性力FDI和空气阻力FDH计算式为
(5)
式中:W=Mg、M、aD、D、VD分别是拖体的重力、质量、加速度、空气阻力系数和速度.
2.2 稳态动力学模型
在稳态时,拖缆位移U=0,u=U/a,其中,a为飞机盘旋半径.即u=0,将U=0、式(1)和式(3)代入方程式(2),通过量纲一化得:
ρk+ω*2[k×(k×r)+dn|vn|vn]
(6)
其中,s=S0/a,p=P/ρ2A0ag,r=xi+yi+zk=R1/a,ρ=ρ1/ρ2,ω*2=aω2/g,t=ωT,dn=Dn/ρ2A0,vn=dr/ds×((k×r)×dr/ds).
在稳态时,拖体位移Ud=U(0,T)=0,ud=Ud/a,即ud=0,将Ud=0和式(5)代入方程式(4),量纲一化得:
wk+mω*2k×(k×r)+dω*2|k×r|(k×r)
(7)
其中,pd=p(0),即pd为s=0时拖缆的张力,w=W/ρ2aA0g,m=M/ρ2aA0,d=D/ρ2A0.
由方程式(6)、(7)得到:
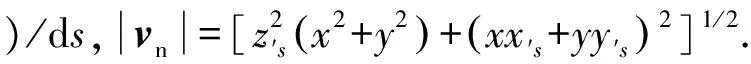
上述量纲一模型的边界条件如下:
在s=0处,
x=Xd/a=xd,y=z=0
式中:Xd为假定拖体在旋转坐标系下的初始Ox轴坐标;xd为计算的假定初值.
在s=L/a=l处,
x2+y2=1,u=U/a
3 拖缆的应用分析
实际应用中,飞机圆周盘旋处于甚低频状态,拖缆的活动区域属于对流层.考虑研究需求和结合实际情况,假设飞机圆周速度v=80 m·s-1;拖缆长度l=5 000 m;拖缆密度ρ1=7 850 kg·m-3;拖缆直径d=2 mm;拖体质量M=50 kg;空气密度ρ2=1.225 kg·m-3;空气摩擦系数cf=0.02;空气压力系数cp=1.2;拖缆离散化数n=20段.
在拖缆系统工作时,飞机以特定的状态进行稳定盘旋飞行[15],飞机速度保持不变,拖缆在一定范围内摆动,拖体保持在中心位置,即悠悠效应.
当系统稳定有效工作时,拖缆进行动态稳定运动,稳定构型的仿真计算结果是呈螺旋形的垂直线,其俯视图如图4所示.从图中可以看出随着飞机的运动,拖缆在水平面内进行稳定的盘旋运动.基于打靶法应用四阶龙格库塔迭代法,对拖缆连续模型的稳态动力学模型进行数值求解,在相同参数下得到量纲一化构型的俯视图如图5所示.可以发现两种方法的构型结果一致,说明所构建的多刚体动力学模型与仿真计算是正确可信的.
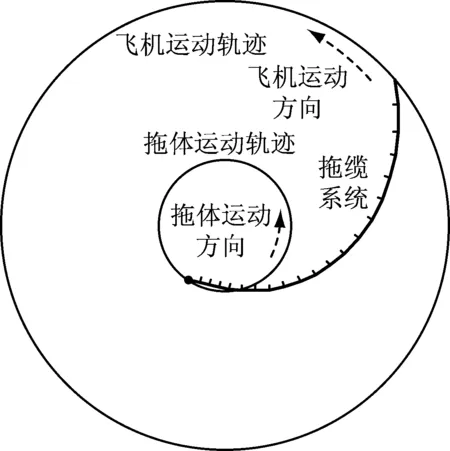
图4 拖缆系统稳定构型俯视图
基于飞机的实际飞行情况,对飞机先直线飞行再转入盘旋轨道运动进行仿真计算,在此过程中不同参数下拖缆垂直长度的变化情况如图6~10所示.从图中可知,飞机状态转换时,拖缆经历了上下大幅摆动的过程,垂直长度的变化过程类似于正余弦波动图,而后逐渐进入工作的运动状态.结果显示仿真600 s过后,拖缆进行动态稳定运动,其垂直长度将趋于保持不变.
不同飞机速度下拖缆垂直长度的变化情况如图6所示,当60 m·s-1 图5 量纲一化拖缆构型俯视图 Fig.5Planeviewoftowedcableconfigurationindimensionlessquantitymethod 图6 不同飞机速度下拖缆垂直长度的变化情况 Fig.6Variationofverticallengthoftowedcableatdifferentspeeds 图7 不同拖缆直径下拖缆垂直长度的变化情况 Fig.7Variationofverticallengthoftowedcableindifferenttowedcablediameter 图8 不同拖体质量下拖缆垂直长度的变化情况 Fig.8Variationofverticallengthoftowedcableatdifferentmassoftowedbody 图9 不同空气密度下拖缆垂直长度的变化情况 Fig.9Variationofverticallengthoftowedcableatdifferentairdensity 不同参数下拖缆垂直度大小如表1所示.可知增加末端拖体质量类似于减少空气阻尼的效果.除飞机速度外,其他参数在一定范围内变化,虽垂直度不同,但都处于系统正常工作范围内.飞机速度临界值在80~90 m·s-1范围内,则应用二分法得出v≤83 m·s-1时满足通信要求.因此,系统要能正常有效通信工作,必须选择合适的飞机速度. 图10 不同空气系数下拖缆垂直长度的变化情况 Fig.10Variationofverticallengthoftowedcableatdifferentaircoefficient 表1 不同参数下拖缆垂直度 (1)针对飞机的圆周盘旋运动,构建了拖缆的多刚体动力学模型.运用数值计算结果对拖缆系统动力学仿真计算的稳态构型进行了验证说明,表明研究方法的正确性. (2)拖缆的垂直长度受飞机和拖体等参数的影响.飞机速度对系统工作的影响最大;为确保垂直度在要求范围内,在一定条件下,应合理减小速度来增大拖缆垂直度;而增加末端拖体质量类似于减少空气阻尼的效果. (3)满足工程实际要求,需确保垂直度始终大于70%,系统正常工作的飞机速度范围是v≤83 m·s-1. [1] 李红泉. 新型航空拖缆制作与检测方法[J]. 兵工自动化, 2014, 33(5): 19. LI Hongquan. Manufacture and test method for a new towing cable[J]. Ordnance Industry Automation, 2014, 33(5): 19. [2] 韩维,侯志强.机载拖曳系统的建模和若干动力学问题[C]∥中国2005年飞行力学与飞行实验学术年会论文集. 西安:飞行力学杂志社, 2005: 1-5. HAN Wei, HOU Zhiqiang. The modeling and some dynamic problem of the trailing cable on an aircraft[C]∥The Flight Dynamic and Flight Experimentation Conference of China. Xi’an: The Flight Dynamic Press, 2005: 1-5. [3] CAUGHEY T K. Whirling of a heavy chain[C]∥Proceedings of the 3rd U.S. National Congress of Applied Mechanics, American Society of Mechanical Engineers. New York: American Society of Mechanical Engineers, 1958: 101-108. [4] LEMON G, FRASER W B. Steady-state bifurcations and dynamical stability of a heavy whirling cable acted on by aerodynamic drag[J]. Proceedings of the Royal Society of London A, 2001, 457(2009): 1021. [5] SKOP R A, CHOO Y I. The Configuration of a cable towed in a circular path[J]. Journal of Aircraft, 1971, 8(11): 856. [6] HUANG S L. Mathematical model for long cable by orbiting aircraft[R]. Johnsville: Naval Air Development Center, 1969. [7] ZHU F, RAHN C D. Stability analysis of a circularly towed cable-body system[J]. Journal of Sound and Vibration, 1998, 217(3): 435. [8] 郑小洪,韩维,贾忠湖,等. 机载拖曳天线动力学建模与仿真[J]. 飞行力学, 2013, 31(3): 234. ZHENG Xiaohong, HAN Wei, JIA Zhonghu,etal. Dynamic modeling and simulation of airborne trailing antenna[J]. Flight Dynamics, 2013, 31(3): 234. [9] CHOO Y I, CASARELLA M J. A survey of analytical methods for dynamic simulation of cable-body systems[J]. Journal of Hydronautics, 1973, 7(4): 137. [10] RUSSELL J J, ANDERSON W J. Equilibrium and stability of a whirling rod-mass system[J]. International Journal of Non-Linear Mechanics, 1977, 12(2): 91. [11] JAMES M C, LOUIS V S, Thomas D S. Dynamic modeling of a trailing wire towed by an orbiting aircraft [J]. Journal of Guidance, Control, and Dynamics, 1995, 18(4): 875. [12] PAUL W, PAVEL T. A study on the transitional dynamics of a towed-circular aerial cable system[C/CD] ∥ AIAA Atmospheric Flight Mechanics Conference and Exhibit. California: American Institute of Aeronautics and Astronautics, 2005. [13] HOERNER S F. Fluid dynamic drag[M]. Bakersfield: Hoerner Fluid Dynamics, 1965. [14] QUISENBERRY J, ARENA A. Dynamic simulation of low altitude aerial tow systems[C]∥AIAA Atmospheric Flight Mechanics Conference and Exhibit. Providence: AIAA, 2004: 4804-4813. [15] BORST R G, GREISZ G F, QUYNN A G. Fuzzy logic control algorithm for suppressing E-6A long trailing wire antenna wind shear induced oscillations[R]. Washington: AIAA, 1993.






4 结论
