低碳视角下中国农业生产技术效率分析——基于产出距离函数的随机前沿方法

王善高

（南京农业大学经济管理学院，江苏 南京 210095）

一、引言

近年来，随着现代农业快速发展，农业温室气体排放呈现出持续增加趋势。IPCC评估报告指出[1]，农业温室气体排放量占全球温室气体排放量的比重已经高达13.5%，成为全球温室气体的第二大来源，农业生产中的碳排放问题已不容小觑。统计数据显示[2]，2011年中国农业生产过程中产生的二氧化碳接近9000万吨，达到历史新高。为了能够降低农业生产中的碳排放量，促进我国农业可持续发展，我国政府适时提出了发展低碳农业和绿色农业的政策。在此背景下，大量学者对农业碳排放问题进行了深入而细致的研究，梳理下来，主要集中在以下几个方面：第一，测算农业碳排放量。如李国志和李宗植[3]、刘华军等[4]、贺亚亚等[5]测算了我国各地区的农业碳排放量，并从时间和空间两个维度分析了农业碳排放的演变趋势，发现我国农业碳排放在时间和空间上存在明显差异。第二，研究农业碳减排机制与政策。如董红敏等[6]对农业主要碳源研究发现，改善反刍动物营养、推广稻田间歇灌溉和推行长效肥料等能够有效降低农业碳排放。Peters等[7]研究发现合理的税费标准与富有弹性的激励政策在一定程度上能够降低农业碳排放量。第三，研究农业碳排放的绩效和碳排放约束下的农业生产率。如高鸣和宋洪远[8]测算了我国各省区1990－2010年的农业碳排放量，并使用ML指数和收敛模型分析了中国农业碳排放绩效的动态变化和收敛等问题。李博等[9]利用中国1998－2012年各省市区的面板数据，采用SBM模型测算了各省市碳排放约束下的农业生产效率。此外，张莉侠和曹黎明[10]、郑恒和李跃[11]、马晓旭[12]还对低碳农业发展所面临的挑战及其未来发展路径进行了阐述。

遗憾的是，现有研究主要从宏观理论和微观农户视角研究农业碳排放，鲜有学者立足于低碳农业视角，将农业碳汇、农业碳排放和农业投入产出纳入到同一分析框架中，系统考察我国低碳农业的发展水平。事实上，农业具有碳汇和碳源双重属性，虽然农用物资的广泛使用会带来温室气体排放，但农作物生产过程中的光合作用也具有固碳作用（吸收二氧化碳）。因此在低碳农业研究中，如果仅仅考虑农业碳排放而不考虑农业碳汇则显得有失偏颇。有鉴于此，本文拟将农业碳排放和农业碳汇同时纳入农业经济增长核算框架，采用产出距离函数的随机前沿分析方法，测算低碳视角下中国农业生产技术效率。本文的主要贡献在于：第一，为了更好地诠释低碳农业理念①低碳农业是低碳经济的重要组成部分，其追求的是低耗、低排、低污和高碳汇，实现农业生产的可持续发展。，在测算农业生产技术效率时，在考虑农业经济产出和农业碳排放的基础上，还引入了农业生态产出，即将农业碳汇作为产出纳入了效率分析方程。第二，本文以狭义农业（种植业）作为研究对象，测算出的低碳农业生产技术效率更精确、更能反映农业生产的真实情况②农业分为广义农业和狭义农业，广义农业包括了农、林、畜、渔和副业，而狭义农业仅指种植业。由于农、林、畜、渔和副业的产值在第一产业产值中的比重存在较大的地区差异，而且广义农业涉及范围广，投入要素的选取存在一定困难，若对广义农业进行效率测算，会存在较大偏误，因此本文选择狭义农业进行效率测算。。第三，分析我国低碳农业生产技术效率的时空差异，并将低碳农业生产技术效率同不考虑碳排放/碳汇时测算出的农业生产技术效率进行系统比较，以期为我国低碳农业的发展和政策制定提供理论参考。

二、研究方法

本文采用的是产出距离函数的随机前沿方法，该模型是以 Battese and Coelli[13]的随机前沿模型和Coelli and Perelman[14]的产出距离函数为研究基础。Battese and Coelli[13]构造的随机前沿生产函数模型为：

其中，i和t分别表示截面数与时期数；y表示农业产出；x表示要素投入；f（xit；β）表示特定函数形式；β为待估的投入向量参数。vit为随机统计误差，表示各种随机因素对前沿产量的影响，服从独立于 uit的正态分布 N（0，σV2）；uit为由技术非效率引起的误差，并服从独立于vit的截断正态分布N＋（m，σu2）。

此后，随机前沿生产函数被各国学者广泛应用于各行各业的效率测算中。但（1）式所示的模型只适用于单产出情形，对于多产出的情形将不再有效。为了解决这一问题，Coelli and Perelman[14]提出了产出距离函数来处理多产出情形。与之类似，本文也从产出距离函数的角度进行分析。假设用K表示投入、M表示产出，则产出距离函数可表示为：

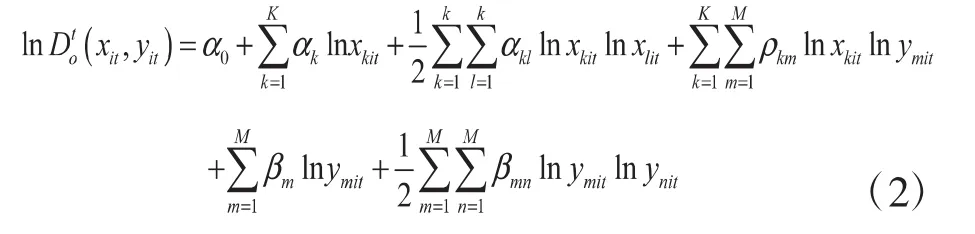
其中，D0t（xit，yit）为t时期技术水平下的产出，xit表示t时期的要素投入，yit表示t时期的产出。

产出距离函数关于yit满足一次齐次性质，因此具有如下约束条件：

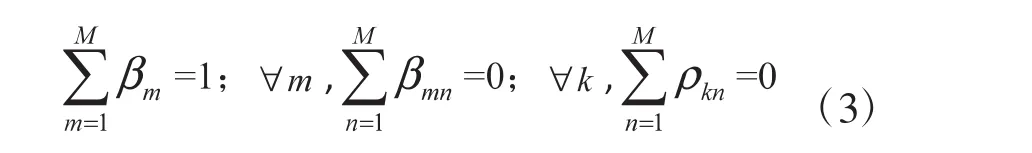
除此之外，投入距离函数还具有对称性条件：

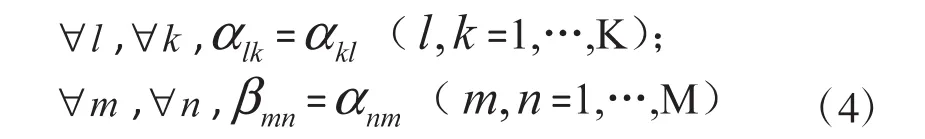
要想使公式（1）同时满足一次齐次性质和对称性条件，需要对原模型的产出进行标准化，即对同时除以某一种产出，得到：

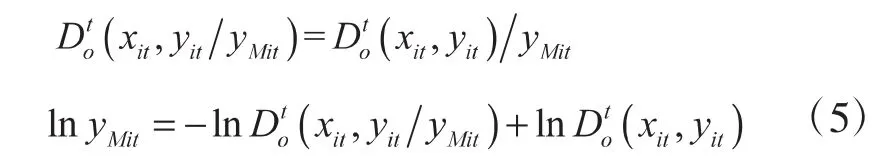
设uit＝－1nD0t（xit，yit），然后在式（5）中加入随机项，即可得到随机前沿模型：

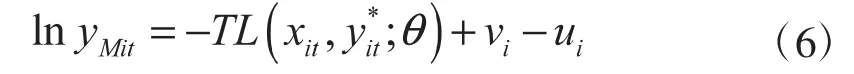
对于由（6）式确定的基于产出距离函数的随机前沿模型可以采用极大似然估计（ML）法来估计参数。得到参数估计值后，可以求解出技术效率，计算公式如下：

在本文的实证分析中，本文构造了一个2产出和5投入的超越对数生产函数，模型形式如下：

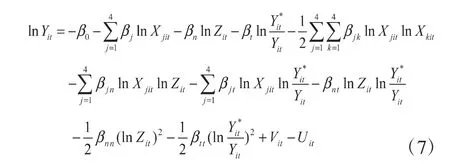
其中，Yit表示农业生产的经济产出，Yit*表示农业生产的生态产出（农业碳汇），Xjit表示劳动、土地等常规要素投入，Zit表示农业碳排放量，参照 Lansink and Reinhard[15]的思想，将其作为一种投入要素处理。

三、数据来源与变量说明

（一）数据来源

基于本文研究目的以及数据的可获得性，本文使用2001－2012年中国31个省（市）的农业生产投入产出数据进行分析，数据来源于《中国统计年鉴》《中国农村统计年鉴》和《中国畜牧业年鉴》。考虑到本文中的农业碳汇主要来源于农作物整个生长周期中的碳吸收，因此按照我国种植业的发展现状，将我国31个省（市）划分为粮食主产区、主销区和平衡区三个区域③划分标准参照财政部和国家粮食局的分类：粮食主产区为：河北、内蒙古、辽宁、吉林、黑龙江、江苏、安徽、江西、山东、河南、湖北、湖南、四川（13个）；粮食主销区为：北京、天津、上海、浙江、福建、广东、海南（7个）；粮食平衡区为：山西、广西、重庆、贵州、云南、西藏、陕西、青海、甘肃、宁夏、新疆（11个）。进行对比研究。其中，粮食主产区以粮食作物种植为主，且粮食产量较多；主销区以经济作物种植为主，粮食自给率较低；平衡区也以粮食作物种植为主，基本实现自给自足[16]。

（二）变量说明

由于本文采用的是超越对数生产函数，如果解释变量选取太多，会使得待估参数过多，最终影响回归结果的收敛趋势。参照大多数学者的思路，选取了如下变量：

1.农业产出变量

（1）农业经济产出。用农业总产值来衡量，并用农业总产值指数进行平减（以2001年为基期），以剔除价格因素的影响。

（2）农业生态产出。需要说明的是，受相关理论以及数据可获得性的限制，本文中的农业碳汇主要指农作物生长过程中的碳吸收（不包含林地和草地）。参照田云和张俊飚[17]、陈罗烨等[18]的计算方法，农业碳汇的计算公式如下：

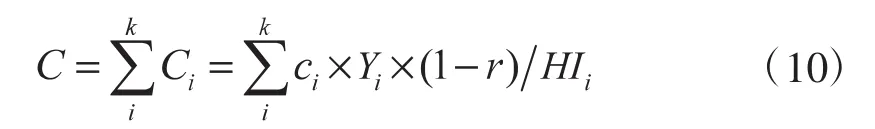
其中，C为农作物碳汇总量；Ci为某种农作物碳汇量；k为农作物种类数；ci为农作物光合作用所能吸收的碳量；Yi为农作物的经济产量；r为农作物的含水量；HIi为农作物经济系数。

2.农业投入变量

（1）土地投入（X1，千公顷）。本文选取农作物播种面积作为土地投入。

（2）劳动力投入（X2，万人）。将历年农业从业人数作为劳动投入指标。由于《中国统计年鉴》仅给出了农林牧渔业从业人员总数，为了估计出农业从业人数，本文参照大多数学者的思路，用权重系数方法将农业从业人数分离出来，具体计算公式为：农业从业人数＝（农业总产值/农林牧渔业总产值）×农林牧渔业从业人员。

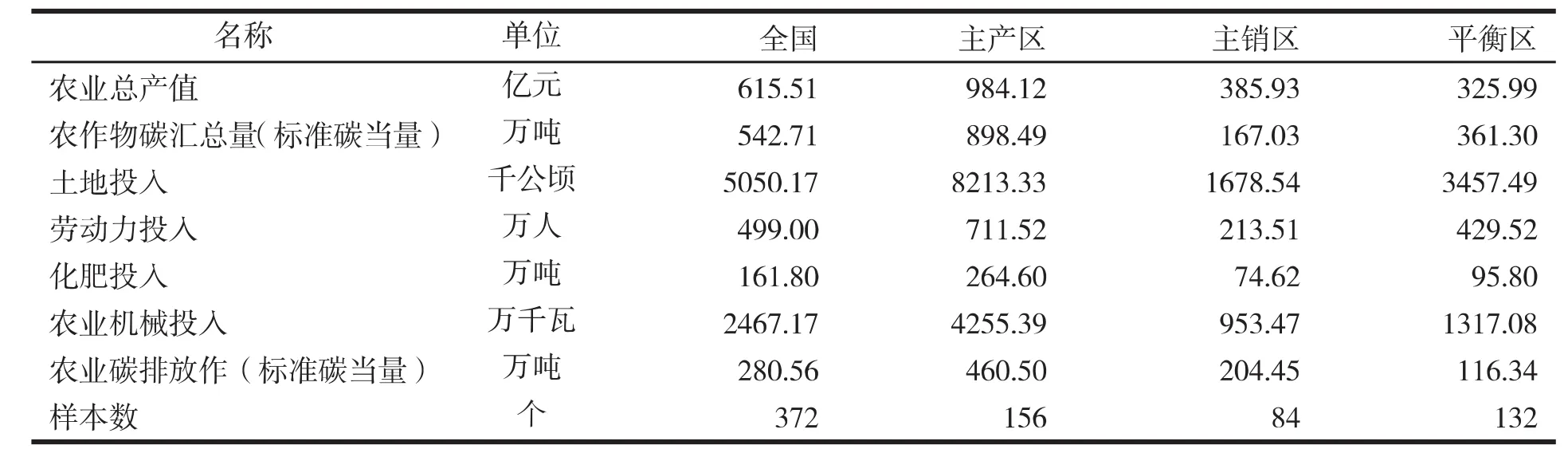
表1 相关变量的描述性统计结果

（3）化肥投入（X3，万吨）。用各省（市）每年的化肥折纯用量（包括氮肥、磷肥、钾肥和复合肥）作为化肥投入指标。

（4）农业机械投入（X4，万千瓦）。用各省（市）每年的农业机械总动力来反映。

（5）“非合意”投入（X5，万吨）。本文将农业生产中的碳排放作为一种非合意投入。参照大多数学者的分析思路并结合本文的研究对象（种植业），从以下两个方面核算农业碳排放④农业碳排放主要来源于三个方面：农用物资投入碳排放、水稻种植所导致的甲烷（CH4）排放和畜禽养殖所引发的碳排放。由于本文以狭义农业（种植业）作为研究对象，故这里不考虑畜禽养殖所引发的碳排放。：一是农用物资投入碳排放，其排放系数出自李波等[19]、田云等[20]和段华平等[21]的相关研究。二是水稻种植所导致的甲烷（CH4）排放，其排放系数主要出自田云和张俊飚[17]的研究成果，该系数充分考虑了水稻种植的地域分布及其生长周期差异，具有较强的科学性。

结合上文分析，采用被国内学者广泛引用的李波等[19]的碳排放测算方法，计算公式为：

其中，F指农业生产过程中的碳排放总量；Fi指各类碳源碳排放量；Ti表示各碳排放源的原始量；σi表示各碳排放源的碳排放系数。在对农业碳排放量进行加总时，为方便分析，本文参照吴贤荣等[22]的思路，依据温室效应强度将二氧化碳、甲烷和一氧化二氮统一转换成标准碳当量⑤IPCC第四次评估报告指出：1吨CO2含0.2727吨C；1吨CH4所引发的温室效应相当于25吨CO2（约合6.8182吨C）所产生的温室效应；1吨N2O所引发的温室效应相当于298吨CO2（约合81.2727吨C）所产生的温室效应。，表1展示了相关变量的描述性统计结果。

四、实证结果与分析

（一）模型检验和估计

Battese and Coelli[23]指出随机前沿模型主要有变差率的单边似然比检验和函数设定形式检验两种。首先，变差率检验考察的是非效率项和随机误差项哪一个影响程度更重要，若γ＝0，则可以忽略非效率的影响。其次，模型设定形式检验主要考察SFA模型是否可以使用C－D形式。针对本文的两个检验，文章均采用似然率检验统计量LR来实现，计算公式为LR＝－2[ln（H0）－ln（H0）]，其中，L（H0）和 L（H1）分别是有约束和无约束条件下的最大似然函数值，且LR服从自由度为n的x2分布，n为约束的个数，统计检验结果见表2。检验结果表明，单边似然比检验⑥要说明的是，由于γ＝0在边界上，其真实分布与普通x2分布相差较大，此时用普通x2分布来检验γ的似然比统计量不可靠，而应采用混合x2分布，它能更好地解决成本效率前沿面上的参数检验问题，混合x2的临界值来自Kodde and Palm（1986）。在1%的水平上通过检验，这说明我国农业生产存在无效率现象，因此需要采用随机前沿生产函数进行实证分析。其次，模型设定形式检验也在1%的水平上显著，说明随机前沿生产函数不可以简化为C－D形式，即需要选择Translog形式。表3展示了随机前沿生产函数的估计结果。

表2 模型设定形式检验

（二）低碳农业技术效率的时空差异

表4展示了2001－2012年中国各地区低碳农业生产技术效率值。首先，从全国范围来看，中国低碳农业生产技术效率均值为0.890，说明当前我国低碳农业生产技术效率处在较高水平，但不可否认，我国农业生产依然存在技术效率损失问题。如果能够消除这种效率损失，在维持当前投入与产出水平不变的情况下，我国农业生产仍有近11%的改善空间。其次，分地区来看，主产区、主销区、平衡区低碳农业生产技术效率的均值依次为0.881、0.909和0.889，呈现出主销区、平衡区、主产区依次递减的趋势。崔晓和张屹山[16]测算的农业生产技术效率也存在相似递减趋势，但他们没有考虑农业生态产出。最后，从时间上来看，无论主产区、主销区还是平衡区，低碳农业生产技术效率均呈现出一定的改善趋势，且这种趋势在主销区和平衡区更为明显。三个地区均出现效率提升的可能原因是，本文的考察期为2001－2012年，时间跨度为12年，在这期间里中国农业生产的生产技术、管理水平和经营方式等都出现了极大改进，因此各地区低碳农业生产技术效率均有所提高。而主产区效率提升的幅度要小于主销区和平衡区的原因在于，主产区大量种植粮食作物（粮食产量占全国总产量70%以上），为了保证粮食产量，必然不可避免的大量使用化肥、农药、农膜和柴油等生产性资料，田云和张俊飚[17]研究发现传统农业大省尤其粮食主产省区是我国农业生产碳排放的主要来源地，13个粮食主产省区中有9个省区的碳排放量居于全国前10，这在一定程度上抵消了由生产技术、管理水平和经营方式等改进带来的效率提升。

（三）低碳农业技术效率与其他技术效率

正如前文所述，农业生产效率的测算是一个不断完善的过程。早期学者测算的农业生产技术效率既没有考虑非合意产出也没有考虑生态产出，随着农业面源污染问题日益严重，学者们开始重视农业生产中的非合意产出，并将其纳入效率测算方程中。但一直以来，鲜有学者在农业生产技术效率的测算中考虑农业生态产出。接下来，本文将分别测算三种方法下的农业生产技术效率，并直观比较三种技术效率的差异。图1为三种方法下测算出的农业生产技术效率的折线图。研究发现，在农业生产方程中，不考虑农业碳排放、碳汇测算出的技术效率要高于仅考虑农业碳排放的技术效率，田旭和王善高[25]的研究中也存在类似的结论，而同时考虑农业碳排放和农业碳汇测算出的低碳农业生产技术效率要明显高于前两种方法测算出的技术效率，即TE（考虑碳排放、碳汇）＞TE（不考虑碳排放、碳汇）＞TE（仅考虑碳排放），说明如果不考虑碳排放、碳汇或者仅考虑碳排放，将会低估我国农业生产技术效率。因此将农业生态产出纳入效率分析方程中测算的低碳农业生产技术效率将更加精确，而且能更好地体现农业的正外部性。

（四）低碳农业技术效率的地区差异

上文的分析结果表明，考虑农业碳排放、碳汇测算出的低碳农业生产技术效率呈现出主销区、平衡区、主产区依次递减的趋势。那么，三个地区低碳农业生产技术效率的差异大小如何呢？这种差异大小是否会随着有没有考虑农业碳排放、碳汇而改变呢？对此，本文将进一步分析。为了方便比较，本文同时汇报了其他两种方法测算下的农业生产技术效率的地区差异（见表5）。结果显示，考虑农业碳排放、碳汇测算出的低碳农业生产技术效率的地区差异要明显小于其他两种方法测算出的农业生产技术效率的地区差异。具体而言，不考虑碳排放、碳汇测算出的主产区、主销区、平衡区农业生产技术效率的差值依次为－0.037、－0.015和0.022；仅考虑碳排放测算出的三个地区农业生产技术效率的差值依次为－0.010、0.046和0.056；而同时考虑碳排放、碳汇测算出的三个地区农业生产技术效率的差值依次为－0.028、－0.009和0.019，说明如果仅考虑农业碳排放，将放大农业生产技术效率的地区差异，而同时考虑农业碳排放和碳汇，将缩小农业生产技术效率的地区差异，这意味着在农业生产中同时考虑农业碳排放和碳汇后，我国各地区的低碳农业生产技术效率将变得相对均衡。

为了便于对比研究，本文对近2年内测算农业（粮食）生产技术效率的文献进行了简单梳理（见表6）。发现虽然测算农业生产技术效率的文献很丰富，但当前学者均忽略了农业生态产出，这说明将生态产出纳入效率分析方程是很有必要的。值得关注的是，总体来看，学者们测算出的技术效率的地区差异都比较大，如赵丽平等[29]测算出的主产区、主销区、平衡区农业生产技术效率的差值依次为0.05、0.06和0.01。造成这种现象的原因除了测算方法、测算对象和测算数据等不同外，本文认为更主要的是他们在农业生产方程中没有考虑生态产出。

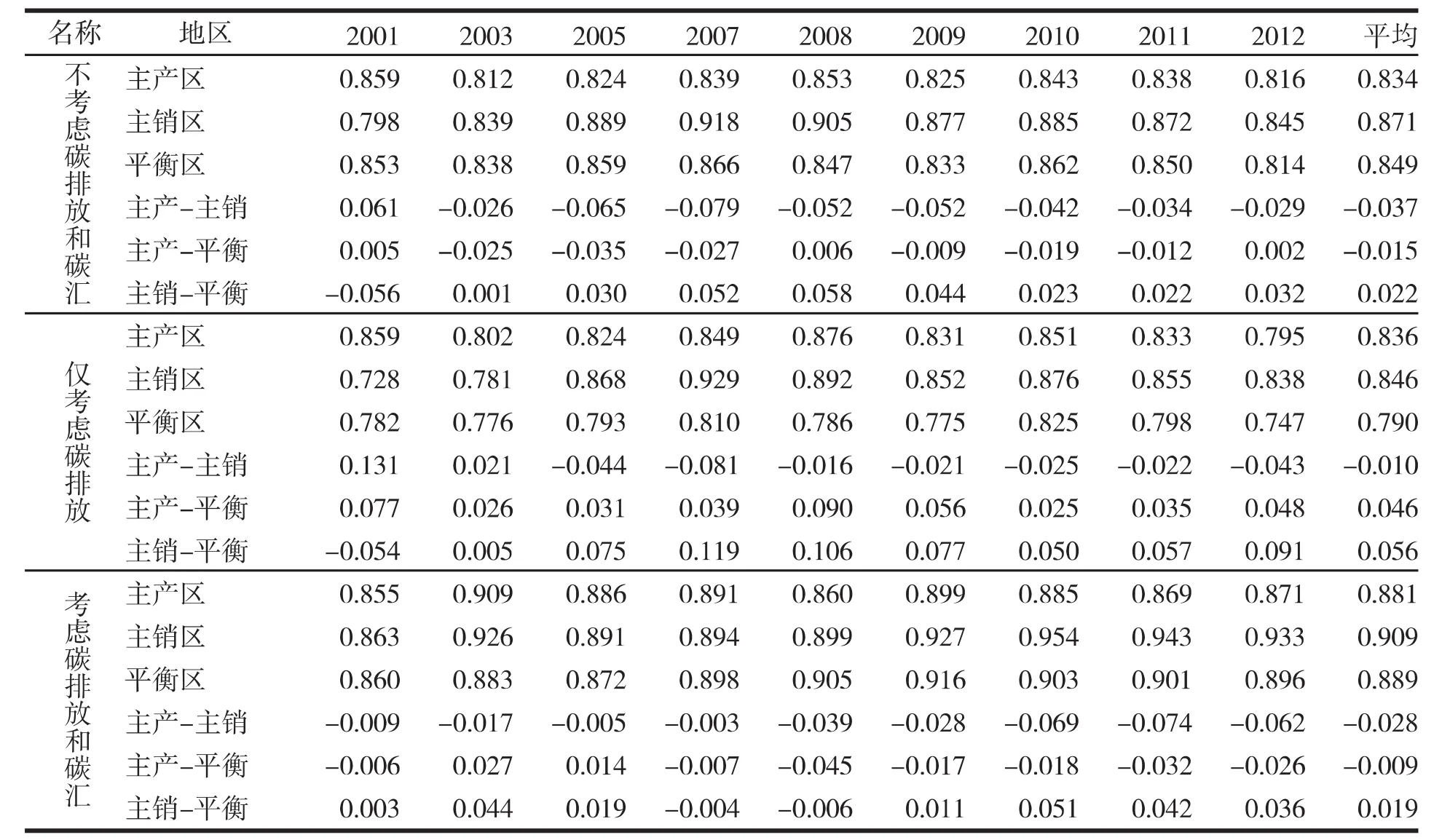
表5 低碳农业技术效率和其他技术效率的地区差异

表6 农业生产技术效率文献的简要梳理

五、结论与启示

（一）结论

本文采用产出距离函数的随机前沿分析方法，将农业碳排放和农业碳汇同时纳入农业经济增长核算框架，测算低碳视角下中国农业生产技术效率，并分析了我国低碳农业生产技术效率的时空差异，而且将低碳农业生产技术效率同不考虑碳排放/碳汇时测算出的农业生产技术效率进行系统比较，主要得出如下结论：

1.全国低碳农业生产技术效率均值为0.890，且呈现出主销区、平衡区、主产区依次递减的趋势，但地区差异相对较小。同时，随着时间变化，各地区的低碳农业生产技术效率均呈现出一定的递增趋势。

2.不考虑农业碳排放、碳汇测算出的技术效率要高于仅考虑农业碳排放的技术效率，而同时考虑农业碳排放和农业碳汇测算出的低碳农业生产技术效率要明显高于前两种方法测算出的技术效率，即TE（考虑碳排放、碳汇）＞TE（不考虑碳排放、碳汇）＞TE（仅考虑碳排放）。

3.考虑农业碳排放、碳汇测算出的低碳农业生产技术效率的地区差异要明显小于其他两种方法测算出的农业生产技术效率的地区差异。

（二）启示

1.农业具有碳源和碳汇双重属性，在测算农业生产技术效率时，需要同时兼顾农业碳排放和农业碳汇，如果仅仅考虑其中的一种，则会低估或者高估我国农业生产技术效率。现阶段来看，兼顾碳排放和碳汇测算出的低碳农业生产技术效率虽然处在较高水平，达到了0.890，但依然存在巨大的提升潜力。从理论上来看，还有11%的提升空间，因此可以采取优化种植结构、创新低碳农业生产技术以及对使用减排技术农户采取补贴政策等措施来提高我国低碳农业生产技术效率。

2.同时考虑碳排放和碳汇后，粮食主产区、主销区、平衡区的低碳农业生产技术效率相对均衡，彼此间差异较小，说明当前我国各地区低碳农业发展相对均衡。特别值得注意的是，TE（考虑碳排放、碳汇）＞TE（不考虑碳排放、碳汇）＞TE（仅考虑碳排放），这提醒我国在进行农业生产时，需要保持各地区低碳农业的平衡发展，避免出现“高碳排、低碳汇”的不均衡现象。

[1]IPCC.气候变化2007：综合报告，政府间气候变化专门委员会第四次评估报告第一、第二和第三工作组的报告[R].日内瓦：IPCC，2007.

[2]田伟，杨璐嘉，姜静.低碳视角下中国农业环境效率的测算与分析——基于非期望产出的SBM模型[J].中国农村观察，2014，（05）：59－71.

[3]李国志，李宗植.中国农业能源消费碳排放因素分解实证分析——基于LMDI模型[J].农业技术经济，2010，（10）：66－72.

[4]刘华军，鲍振，杨骞.中国农业碳排放的地区差距及其分布动态演进——基于Dagum基尼系数分解与非参数估计方法的实证研究[J].农业技术经济，2013，（3）：72－81.

[5]贺亚亚，田云，张俊飚.湖北省农业碳排放时空比较及驱动因素分析[J].华中农业大学学报（社会科学版），2013，（5）：79－85.

[6]董红敏，李玉娥，陶秀萍，等.中国农业源温室气体排放与减排技术对策[J].农业工程学报，2008，24（10）：269－273.

[7]Peters M，House R，Lewandrowski J，et al.Economic impacts of carbon charges on U.S.agriculture[J].Climatic Change，2001，50（4）：445－473.

[8]高鸣，宋洪远.中国农业碳排放绩效的空间收敛与分异——基于Malmquist－luenberger指数与空间计量的实证分析[J].经济地理，2015，35（4）：142－148.

[9]李博，张文忠，余建辉.碳排放约束下的中国农业生产效率地区差异分解与影响因素[J].经济地理，2016，36（9）：150－157.

[10]张莉侠，曹黎明.中国低碳农业发展现状与对策探讨[J].经济问题探索，2011，（11）：103－106.

[11]郑恒，李跃.低碳农业发展模式探析[J].农业经济问题，2011，32（6）：26－29.

[12]马晓旭.我国低碳农业发展的困境及出路选择[J].经济体制改革，2011，（5）：71－74.

[13]Battese G E，Coelli T J.A model for technical inefficiency effects in a stochastic frontier production function for panel data[J].Empirical Economics，1995，20（2）：325－332.

[14]Coelli T，Perelman S.A comparison of parametric and non－parametric distance functions：With application to European railways[J].European Journal of Operational Research，1999，117（2）：326－339.

[15]Lansink A O，Reinhard S.Investigating technical efficiency and potential technological change in Dutch pig farming[J].Agricultural Systems，2004，79（3）：353－367.

[16]崔晓，张屹山.中国农业环境效率与环境全要素生产率分析[J].中国农村经济，2014，（8）：4－16.

[17]田云，张俊飚.中国农业生产净碳效应分异研究[J].自然资源学报，2013，28（8）：1298－1309.

[18]陈罗烨，薛领，雪燕.中国农业净碳汇时空演化特征分析[J].自然资源学报，2016，31（4）：596－607.

[19]李波，张俊飚，李海鹏.中国农业碳排放时空特征及影响因素分解[J].中国人口资源与环境，2011，21（8）：80－86.

[20]田云，张俊飚，李波.中国农业碳排放研究：测算、时空比较及脱钩效应[J].资源科学，2012，（11）：2097－2105.

[21]段华平，张悦，赵建波，等.中国农田生态系统的碳足迹分析[J].水土保持学报，2011，25（5）：203－208.

[22]吴贤荣，张俊飚，田云，等.中国省域农业碳排放：测算、效率变动及影响因素研究——基于DEA—Malmquist指数分解方法与Tobit模型运用[J].资源科学，2014，36（1）：129－138.

[23]Battese G E，Coelli T J.Frontier Production Functions，Technical Efficiency and Panel Data：With Application to Paddy Farmers in India[J].Journal of Productivity Analysis，1992，3（1）：153－169.

[24]Kodde D，F Palm.Wald Criteria for Jointly Testing Equallity and Inequality Restrictions [J].Econometrica，1986，54（5）：1243－1248.

[25]田旭，王善高.中国粮食生产环境效率及其影响因素分析[J].资源科学，2016，38（11）：2106－2116.

[26]马林静，欧阳金琼，王雅鹏.农村劳动力资源变迁对粮食生产效率影响研究[J].中国人口资源与环境，2014，24（9）：103－109.

[27]高鸣，宋洪远.粮食生产技术效率的空间收敛及功能区差异——兼论技术扩散的空间涟漪效应[J].管理世界，2014，（7）：83－92.

[28]马林静，王雅鹏，吴娟.中国粮食生产技术效率的空间非均衡与收敛性分析[J].农业技术经济，2015，（4）：4－12.

[29]赵丽平，侯德林，王雅鹏，等.城镇化对粮食生产环境技术效率影响研究[J].中国人口资源与环境，2016，26（3）：153－162.