基于集合论估计的水轮机调速建模
2018-02-05谢子骏温步瀛王怀远
谢子骏, 温步瀛, 陈 冲, 王怀远
(福州大学 电力系统与自动化学院,福建 福州 350100)
0 引言
对水轮机原动机及其调速系统[1]的精确建模,对于水轮发电机组的安全稳定运行发挥着巨大的作用。水轮机模型的搭建以及其参数的精确辨识不仅是电力系统中机组调节控制规律[2]的设计研究基础,并且对于电力系统分析、运行、规划和控制器参数优化[3]设计有着重要工程实用价值及理论意义。
由于水轮机工况时变,水轮机调节系统的动态响应与不同工况下的PID参数具有很强的关联性。因此,水轮机与其调节系统数学模型[4]的深入研究关乎到了水轮机组是否能够稳定运行,水轮机组动态响应过程是否良好,动态响应的品质是否达到所需要要求的重要课题。文献[5]提出了一种电力大数据的服务平台,并且提供大量实验数据支持,但所有数据未经过很好的数据优化处理。从实测数据的角度来看,《电力系统安全稳定导则》[6]中明确规定在进行电力系统计算时,需采用实测参数,而实测参数中包含了大量的不良数据[7],对于如何去除不良数据,是水轮发电机及其调速系统参数辨识的研究重点之一。从辨识理论的角度来看,水轮发电机及其调速系统模型是参数辨识的前提条件,文献[8]提出了一种步进式频率扰动的辨识方法,该种扰动方法虽然可行,但由于该方法的不稳定性,不能得到广泛地应用。水轮机系统建模可以分为机理建模[9]和统计建模[10]。水轮机及其调速系统各环节的物理结构经过多年的研究,其物理结构清晰,并且系统的模型结构可以通过机理分析搭建,在模型中尚有的未知参数也可通过辨识方法得出。因此,水轮机各环节的模型结构是其参数辨识的前提与基础。
1 调速系统结构
水轮机调速器[11]包括控制部件和执行部件,控制对象为水轮机以及水轮机的引水系统和发电机负载等,习惯把调速器和调速器的控制对象统称为水轮机调速系统,其结构如图1所示。
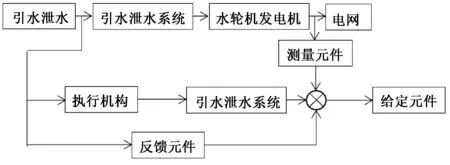
图1 水轮机调速系统
2 调速器工作原理及参数测试
水轮机调速系统包括微机部件、机械液压部件、有压引水管道、水轮机组、发电机和负载等[12-13]。总体而言,可以分为3部分进行讨论研究。
2.1 调节控制系统模型参数
调速系统结构[14]如图2所示。

图2 调速控制系统框图
频率死区ε=±0.05 Hz、功率死区±0.05 MW,Kp、Ki分别表示比例放大系数、积分放大系数,ep表示调差系数,PID_OUT表示控制系统开度指令输出,不设一次调频上下限;前馈系数K2是导叶开度及水头的函数,为变参数,具体以动态一次调频扰动试验辨识所得数值为准。频率死区计算方法:当频差绝对值大于等于0.05 Hz时,实际作用频差要扣除死区的0.05 Hz;当频差绝对值小于0.05 Hz时,死区不起作用。
2.2 执行机构控制系统模型
电液伺服系统[15]由PLC伺服卡、主配压阀、主接力器、导叶等构成。其模型如图3所示。
其中VELOPEN、VELCLOSE分别表示过速开启最大速度、过速关闭最大速度;TR表示主接力器开度反馈时间常数,一般TR=0.02 s;PMAX、PMIN分别表示最大、最小输出功率;TO、TC分别表示执行机构全开时间、全关时间;KP、KV、T1V分别表示执行机构伺服卡比例放大系数、微分放大系数、微分时间常数;PCV、PGV分别表示导叶开度指令、导叶开度反馈。
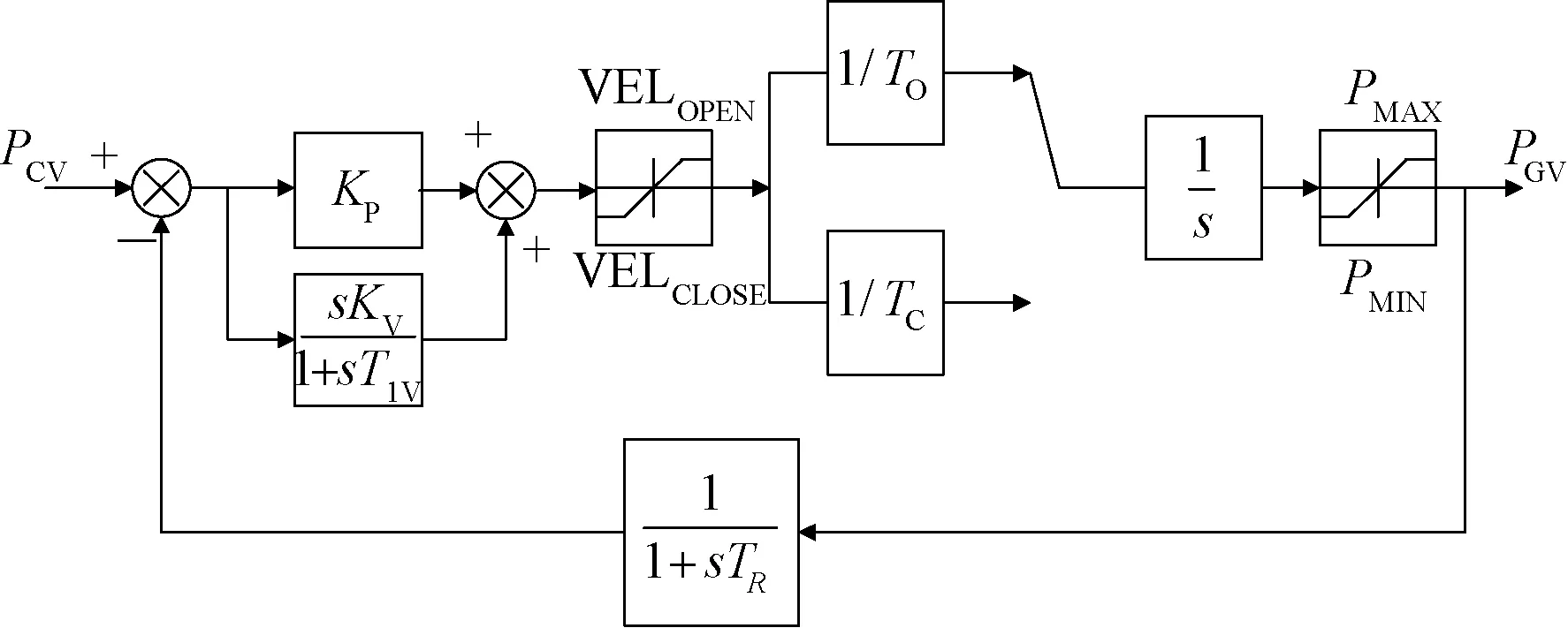
图3 执行机构控制系统模型
2.3 调速器协联关系参数的测试
混流式水轮机[16]属于单调节机组,轴流转桨式机组属于双调节机组。在对双调节机组调速器进行现场测试时,如果没有两套机械液压部件,经常使用混流式机组控制模型代替轴流式机组来进行测试,这种测试方法忽略了协联关系[17]的影响,因而是不够精确的。
轴流转桨式和贯流式机组的桨叶主接行程为当前水头和导叶开度的函数z=f(H,y)。两者的输出均作为后一级机组段的输入量。系统结构如图4。

图4 轴流转桨式机组调速器机械液压部件结构图
2.4 水轮机模型
在研究小波动时,水轮机原动机可线性化展开如式(1):
(1)
当过水系统模型考虑为刚性水锤时即为式(2):
(2)
对于理想的水轮机模型,即水轮机无损失,则ey=1.0,eqh=0.5,e=1.0。则如式(3):
(3)
3 集合论估计
由于现有估计方法中都未考虑到估计值与真值的关系,所以在实践中可以发现,实时数据的可信性不能达到闭环控制所需要的效果。为了能够达到闭环控制的要求,引入集合论估计[18]的思想,通过对系统可用信息的梳理分析,建立模型,增加系统实时数据的可信性。
3.1 存在的根本问题
现有的参数估计方法中,目标函数的确定往往都是追求于目标与量测值的残差值最小,但是残差最小,在实践中往往不能够达到系统所要求的精度,因为残差最小并不意味着估计结果与真值状态就相近,某些时候反而会使估计结果偏离真值状态。
基于“残差最小”理念算法得到的结果如图5,基于“最多测点赞同”理念算法得到的结果如图6。

图5 基于残差最小算法得到的结果

图6 基于最多测点赞同算法得到的结果
由两者可知,残差最小虽然可以使估计值与量测值接近。但是,由于不良测点的存在,估计结果会偏离真值,而采用最多测点赞同的方法,先辨识出不良测点后,在对系统进行状态估计,估计状态就与真实状态接近,进而增加了估计结果的可信度。但此方法仍然存在一定风险,因为得到的估计状态仅为系统的一个可能情况,是否存在更为真实的状态需要经过大量数据以及多次参数估计测试进行比对。
3.2 可行的解决思路
由于状态估计结果与真值未有显示的关系,在实践中状态估计有可能会偏离真值结果,如果能够建立状态估计与真值的关系,那么可得到较为可靠的估计结果。假设估计结果可表示为一个包含真值的集合,利用先验知识,辨识出不良测点,则估计结果与真值的偏差可以界定,这样估计结果的可信度可以得到质的提升。
在状态估计中可用信息主要包括系统拓扑结构t、网络参数P、以及量测数据Z,量测方程Z=h(x,t,p)=0,以及物理约束g(x,t,p)=0和l(x,t,p)=0,其中x为状态向量。集合论估计模型的解集X表示为式(4):
(4)
对于水轮机而言,拓扑结果、网络参数可知,则可以进一步简化解集X表达式为式(5):
(5)
3.3 水轮机的数学模型
考虑到非弹性水锤效应[19],具有非最小相位特征的经典水轮机调速系统模型为式(6):
(6)
式中:ΔPm为水轮发电机机械功率偏差值;Δu为水门开度偏差值;Ts为水门随动系统的时间常数;TW为水击时间常数;u为输入到随动装置的调节控制信号。
对于轴流转桨式水轮机来说,水门开度包括导叶开度与桨叶开度两部分,而导叶开度与桨叶开度满足z=f(H,y),假设在某个时段,水轮机的平均水头H为恒定值,则式中u=g(z,y),则由(6)得式(7):
P2主要与注意资源的分配及对刺激的加工分析有关[13]。本研究发现,在由新异刺激诱发的P2波幅上,术后化疗前组低于化疗组和健康对照组,说明该组患者对分心刺激的抑制不够,从而可能减少对靶刺激的注意资源的投入。
(7)
4 自适应变异粒子群算法
PSO算法[20]存在局部收敛的问题,引入变异因子思想对其改进,目标函数如(8)所示:

(8)
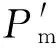
粒子速度和位置更新如(9):
pop=pop+V
(9)
式中,V是粒子的速度,pop是粒子的当前位置,rand是[0,1]之间的随机数,c1和c2为学习因子。
考虑到粒子在当前gbest的作用下可能会寻找到更好的位置,引入变异因子,对满足变异条件的gbest按一定概率变异。计算公式如(10)所示:
(10)
式中,k取[0,1]之间的任意数值。
gbest=gbest*(1+0.5G)
(11)
式中,G为[0,1]之间的随机数值。
5 算例分析
对某水电厂发电机组原动机进行参数测试和建模试验。
发电机的系统参数如表1。

表1 发电机参数
5.1 调节系统控制模型参数辨识
模拟并网状态,在导叶52%开度下,将PID分别设置成纯比例环节,频率死区设成0.05 Hz,在频差输入口强制输入0.25 Hz频差信号,实测功率PID输出结果以及仿真结果如图7所示。在导叶52%开度下,将PID设置成纯积分环节,频率死区设成0.05 Hz,在频差输入口强制输入0.2 Hz频差信号,实测功率PID输出结果以及仿真结果如图8所示。

图7 调速系统纯积分试验数据图

图8 调速系统纯比例试验数据图

图9 调速系统积分调差试验数据图
模拟并网状态,在导叶52%开度下,将PID设置成积分调差反馈环节,频率死区设成0.05 Hz,在频差输入口强制输入0.2 Hz频差信号,实测功率PID输出结果如图9。
参数辨识结果:Ki=6.998,Kp=4.001,bp=3.5%。
5.2 调速器机械液压部件参数辨识
由于测试全开全关时间在滤波仪上进行辨识,本文直接给出测试过的液压部件的全开全关时间如表2。

表2 机械液压部件全开全关时间表
导叶开度给定+5%阶跃仿真,实测数据与仿真数据的对比曲线如图10。

图10 导叶开度给定+5%阶跃数据图
桨叶开度给定+5%阶跃仿真,实测数据与仿真数据的对比曲线如图11。
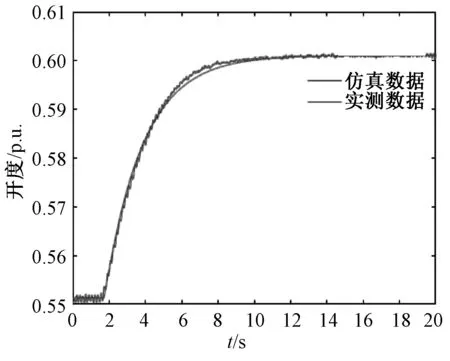
图11 桨叶开度给定+5%阶跃数据图
导叶、桨叶的执行机构控制器中的电液伺服机构PID控制参数辨识结果如表3所示,误差结果对比如表4、5所示。

表3 导叶、桨叶参数辨识

表4 导叶参数性能
5.3 水轮机模型参数识别
本算例中的水轮机参数模型由于其内部构造的特殊性,在Matlab中搭建了二阶模型更能反应出其真实状态,模型如式(12)所示:
(12)
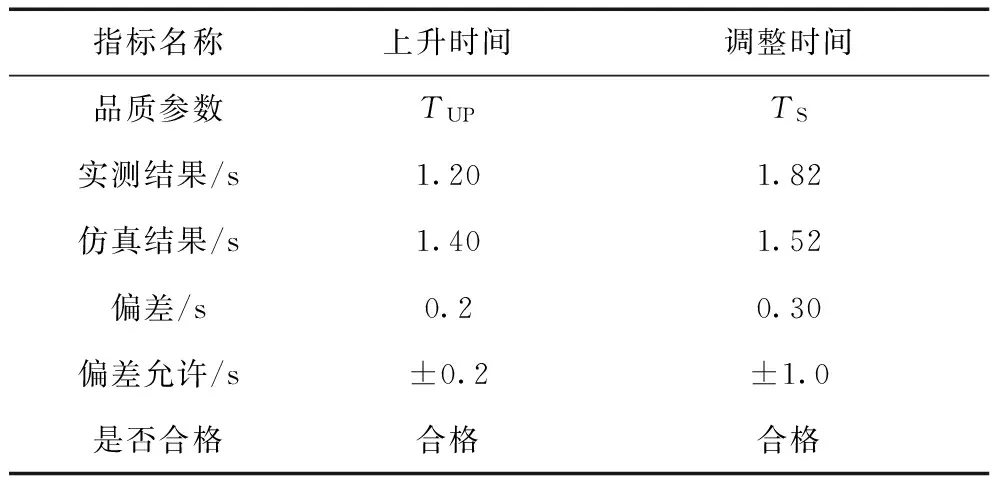
表5 桨叶参数性能
水轮机实测波形有较多毛刺,不方便后续进行运算,先对数据进行滤波处理,滤波前后对比数据图如图12所示。
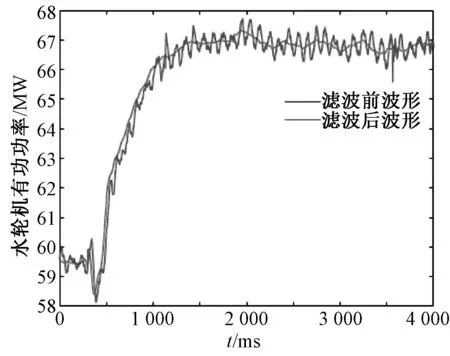
图12 水轮机滤波前后的实测数据
根据式(7)辨识系统中的离群点,对比图如图13。
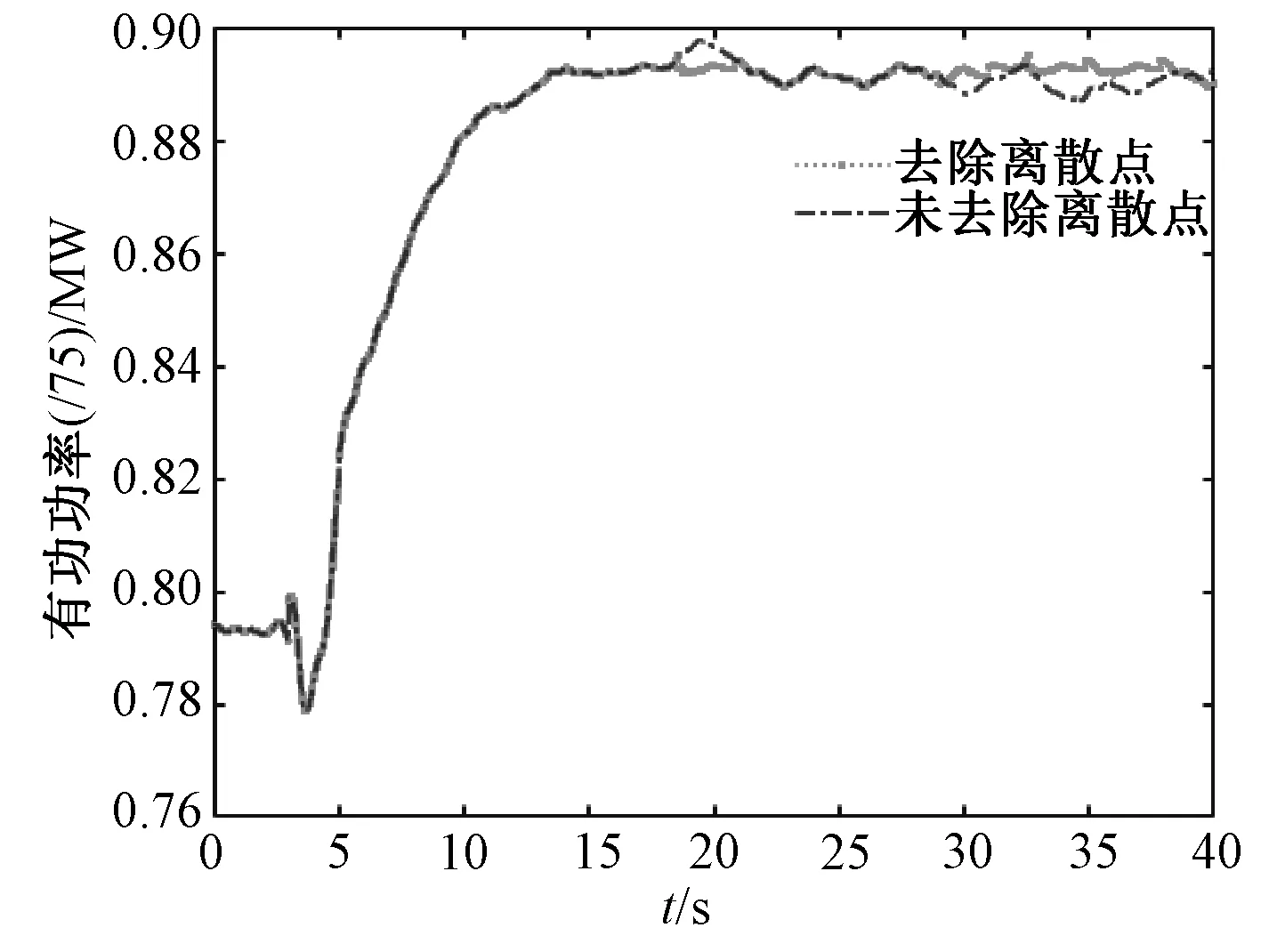
图13 水轮机去除离散点前后波形对比
在未去除离散点与去除离散点两种情况下,分别对两种情况进行参数辨识,辨识结果如图14所示。
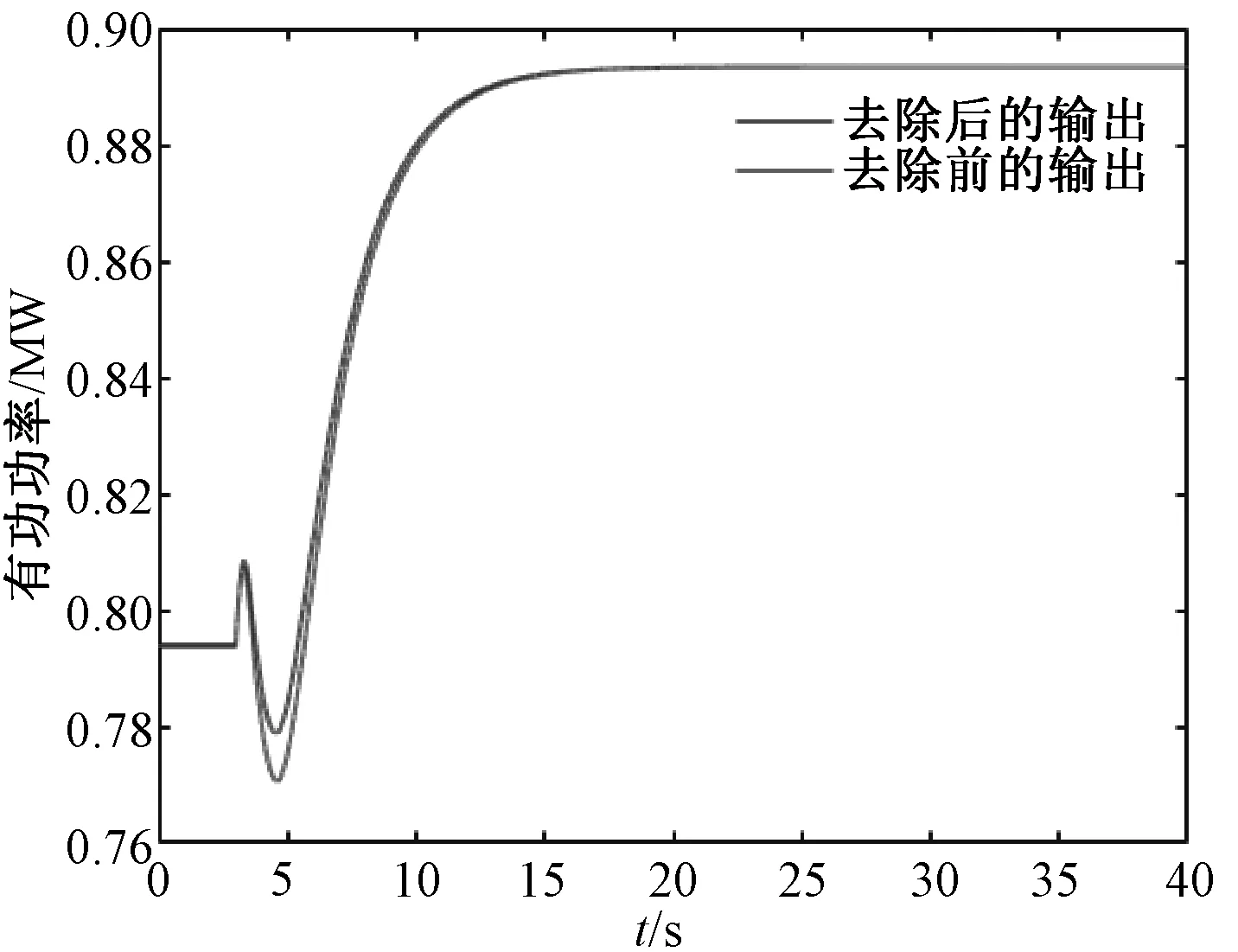
图14 去除离散点前后仿真数据对比
由表6所示,不含离散点的参数明显优于含离散点的参数,且各参数与最优解更相近,可以看出通过集合论估计去除离散点后使得整体曲线误差更小。 图15为在BPA中发电机、励磁模型采用实测参数。水轮机及其调节控制系统模型参数采用5.3节中结果。在功率闭环模式下进行一次调频试验的仿真,仿真结果与实测结果对比如表7所示。
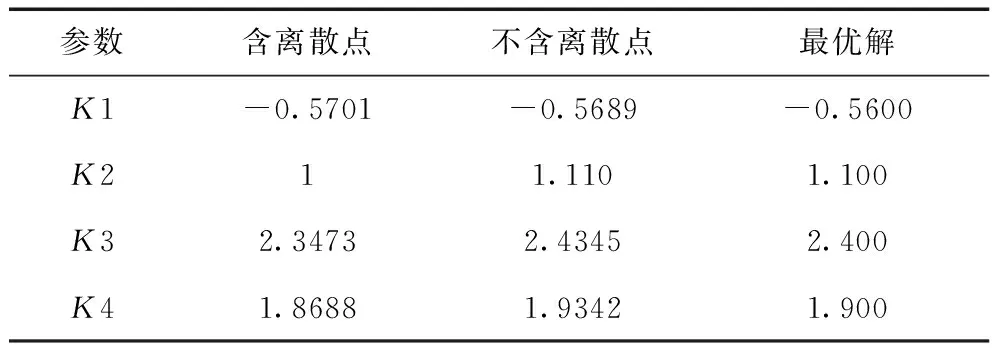
表6 参数辨识结果
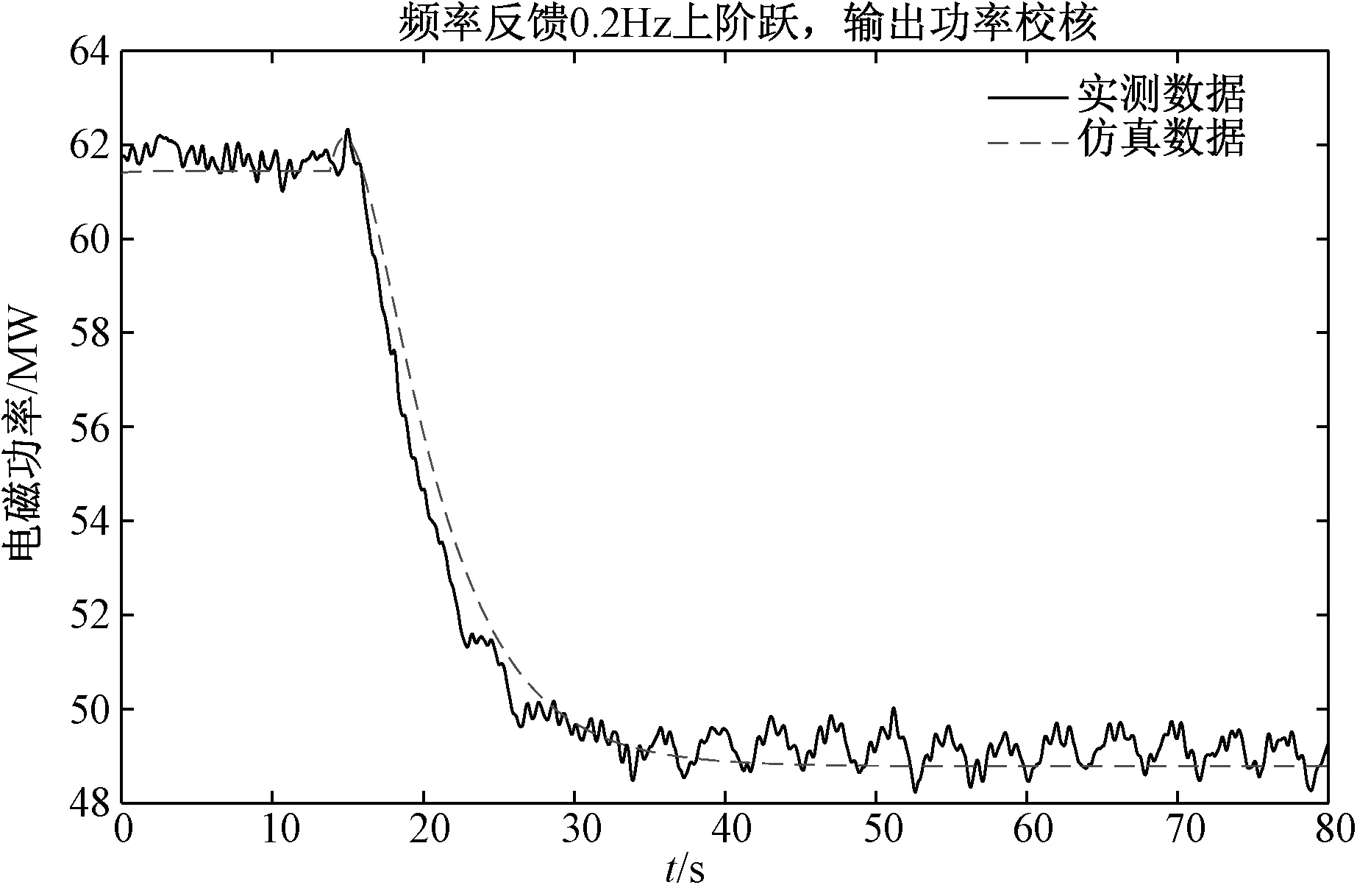
图15 频率反馈0.2 Hz上阶跃仿真与实测对比
由表7可以看出,在功率闭环模式下进行一次调频仿真效果满足系统要求,且比传统的BPA模型误差更小。

表7 各参数比对结果
6 结论
(1)提出了用集合论估计的方法应用于水轮机调速系统参数辨识,由于辨识了离群点,使得结果更加可靠,尽管辨识得到的参数不一定为最优解,但是满足了系统响应的各项指标要求,并且优于传统的辨识方法,更具有实用性。
(2)针对水轮机机组,在MATLAB中搭建了二阶水轮机模型,相较于传统的BPA中水轮机模型更具有一定的优势,并且更能反映出水轮机组工况中复杂的水锤效应。
[1]魏守平,伍永刚,林静怀.水轮机调速器与电网负荷频率控制:(一)水轮机控制系统的建模及仿真[J].水电自动化与大坝监测,2005,29(6):18-22.
[2]魏守平,卢本捷.水轮机调速器的PID调节规律[J].水力发电学报,2003(4):112-118.
[3]张民, 应巧萍. 一种PID控制器参数优化方法: 201310606746.2[P].2014-3-19.
[4]李啸骢, 郑涛, 梁志坚,等. 水轮机水门、励磁与电气制动系统非线性综合控制[J]. 电力自动化设备, 2016, 36(7):97-103.
[5]李栋华,耿世奇,郑建.能源互联网形势下的电力大数据发展趋势[J]. 现代电力,2015,32(5):10-14.
[6]赵遵廉. 《电力系统安全稳定导则》学习与辅导[M]. 北京:中国电力出版社, 2001.
[7]孟娜. 电力用户用电信息采集系统不良数据分析研究[J]. 中国经贸, 2014(11):171.
[8]美莹莹 ,陈光大,孟佐宏,等. 一种基于频率信息扰动的水轮机模型辨识方法[J].大电机技术,2010,32(5):52-56.
[9]房汉鸣, 税爱社, 包建明,等. 机理与实验结合的对象建模方法研究[J]. 自动化与仪器仪表, 2016(1):160-162.
[10]林静, 唐国强, 覃良文. 基于小波分析与贝叶斯估计的组合统计建模[J]. 桂林理工大学学报, 2017, 37(1):217-222.
[11]孔繁镍, 马伏花, 李燕,等. 低通滤波PID水轮机调速系统设计[J]. 控制工程, 2016, 23(2):173-177.
[12]冯雁敏, 王湛, 张雪源,等. 基于混沌粒子群算法的水轮机调速系统参数辨识及建模试验[J]. 长江科学院院报, 2016, 33(8):138-143.
[13]吴成. 水轮机及其调速系统建模与参数辨识[D]. 保定:华北电力大学, 2015.
[15]陈光荣, 王军政, 汪首坤,等. 自适应鲁棒控制器设计新方法在电液伺服系统中的应用[J]. 自动化学报, 2016, 42(3):375-384.
[16]门闯社, 南海鹏. 混流式水轮机外特性与几何尺寸的关系研究[J]. 西安理工大学学报, 2016, 32(2):226-231.
[17]蒋致乐, 郑凯. 协联曲线优化对影响轴流转桨式水轮机效率的探讨[J]. 引文版:工程技术, 2015(27):236-236.
[18]何光宇, 常乃超, 董树锋,等. 基于集合论估计的电网状态辨识(一)建模[J]. 电力系统自动化, 2016,40(5):25-31.
[19]顾承庆, 林婕宇. 发电机技术供水管水锤现象分析[J]. 水电与抽水蓄能, 2016, 2(6):47-51.
[20]余仁波, 赵修平, 孟凡磊. 一种带变异算子的 PSO 算法[J]. 舰船电子工程, 2016, 36(10):26-29.
