基于多目标采购优化的电力供应商选择研究

周鹏程， 吴南南， 曾 鸣

(华北电力大学 经济与管理学院, 北京 102206)

0 引言

原材料供应商作为供应链中的关键环节，是企业进行采购活动的对象，直接关系着企业的竞争能力和营销能力[1-2]。优质高效的电力物资作为电力行业的运行基础[3]，为发电企业满足社会用电需求，保证发电质量与服务水平提供了有力保障。因此，如何对电力物资供应商做出正确地评价，从而科学、合理的进行选择，为发电企业制定采购决策提供依据，已成为各国发电企业十分关注的问题。

目前，国内外对供应商选择的采购优化问题已进了行较为全面地研究。文献[4]通过研究有关供应商选择的文献发现大多数文献中都提到了价格、交货期、质量和能力等评价标准，并采用数学规划法以最低成本为目标函数求解各供应商的供应量和采购成本。文献[5]建立了模糊技术与TOPSIS法相结合的模型，为国外某燃气公司选择供应商提供采购优化决策。文献[6]针对电力物资集中采购提出了多阶段迭代修正的动态采购模型。文献[7-8]从供应商的整体能力等方面构建了供应商评价指标体系，并建立了基于熵权分析模型和模糊物元模型的电力物资供应商选择模型。文献[9]考虑产品和服务质量，构建了精细化的电网物资供应商评价指标体系，通过TOP-GRD分析模型计算相似贴近度以此进行供应商评价。文献[10]建立了基于电力工程EPC总承包物资采购供应商评价指标体系，结合AHP和熵权法确定综合权重，采用TOPSIS法对电力物资供应商进行了综合评价。此外，文献[11]针对应急物资的特点，构建了基于灰熵综合评价的电力设备应急物资采购优化模型。上述文献对于电力物资供应商选择的研究，虽建立了不同的评价模型，但未充分考虑影响供应商选择的因素和限制条件。

科学、合理地选择供应商，将直接影响到企业降低采购成本、优化资源分配、增强稳定运行[12-13]。目前，随着社会用电需求快速增长，发电商作为电力行业的上游企业，应更加强调电力物资采购的质量、交货可靠性、价格、提前期等保障，这也增加了供应商选择的复杂性和选择范围。而发电企业对煤炭等物资的规模化采购与发电量需求需要平衡，以及如何在最小采购成本的目标下对物资供应商进行科学的选择，需要进行更为深入的研究。

鉴于此，本文在前人研究的基础上，综合考虑采购成本、产品质量、交货期时间和循环期时间等影响因素，利用层次分析法与多目标线性规划相结合的方法建立采购优化求解模型，通过算例得到企业的最优化采购方案。

1 目标函数与限制条件

1.1 问题假设

作为发电企业，电力物资如煤炭等应由若干供应商提供，且每家供应商也应供应多家发电企业。假设煤炭供应链中有j(j∈[1，J])家供应商，供货周期为[1，T]，且每家供应商的可供应数量为g(g∈[1，G])；i(i∈[1，I])家发电企业，从j家供应商处采购k(k∈[1，K])种原煤以满足i家发电企业生产需求。各发电企业根据实际生产需求情况和原煤市场价格状况，向供应商提出在某时段t(t∈[1，T])内的采购数量rjki(t)和交货时间dkg(dkg∈[1，T])。

1.2 目标函数

本文提出了一种综合考虑采购成本、产品质量、交货时间和循环时间为影响因素的多目标采购优化模型。即在满足日发电量的前提下，依据各发电企业的需求合理制定出煤炭等电力物资的采购方案，以实现采购成本、产品质量、交货期时间、循环期时间最优化。考虑各影响因素的目标函数如下：

(1)采购成本最小化

假设采购成本的目标函数为fa，发电企业的采购成本由原煤价格、运输成本、各种税费等费用组成。因此，最小化采购成本为：

(1)

式中：Cjki为采购原煤总单位成本，单位为元/t。该成本由原煤单位成本Cjki、单位运输成本Sjki和相关税费Fjki组成，即Cjki=Cjki+Sjki+Fjki。

(2)不合格率最小化

通常，产品质量是供应商选择的一项重要因素。在煤炭等物资的供应中，造成产品不合格的指标主要有含煤量过低，氟、汞、灰分含量超标等问题，直接影响到发电质量及煤炭燃烧充分性。因此，企业在采购时应尽量降低这些不合格率。假设交货期的目标函数为fb，其最低不合格率为：

(2)

式中：Hjki为j家供应商提供给i家发电企业的k种原煤的不合格产品率。

(3)交货期时间最短化

假设交货期的目标函数为fc，其最短化交货时间主要考虑j家供应商的诚信程度、交货历史记录和有无延期等因素。因此，最短交货期时间为：

(3)

式中：Yjki为供应商提供给i家发电企业的k种原煤的不按期交货率。

(4)循环期时间最短化

设循环期时间的目标函数为fd，该时间主要反映各节点供应商对下游节点企业需求的响应程度。由于订单响应时间为一个不确定的区间值，在实际算例中无法估量给出，因此本文忽略了订单响应时间，假设规划模型中实行就近采购策略，仅单独考虑运输时间，最短循环期时间为：

(4)

式中：Xjki为j家供应商到i家发电企业的所需运输时间，单位为h。

1.3 限制条件

对于供应商而言，j家供应商向i家发电企业供应电力物资时，一方面要满足各企业日发电量约束，即在给定的时间t内保证发电企业电力生产所需最低的煤炭数量，如公式(5)所示。另一方面，各物资供应商的供货能力不是无限制的，因此在某时段t(t∈[1，T])内供应量也是有限的，这决定了煤炭采购数量不能超过给定供应数量上限，如公式(6)所示。

(5)

式中：Qkj(t)为发电企业i在某时段t内对k种的原煤需求量，单位为t。

(6)

式中：Pjk(t)为供应商j在某时段t内能够供应的k种原煤供给量上限值，单位为t。

对于发电企业而言，其电力物资采购支出应在合理的预算费用范围内，且应满足企业日发电量所需的原煤采购数量，如公式(7)所示。

(7)

式中：B为总采购预算费用，单位为元。

2 多目标采购优化模型及求解流程

2.1 构建模型

(1)MOLP模型

目前，针对供应商选择优化问题的方法有多种，如基于直觉模糊集VIKOR和基于PCA-BP神经网络等方法求解[14-15]。本文在考虑模型中各种限制条件的基础上，采用线性加权的方法构建了多目标线性规划模型(MOLP)，并基于Lingo V14.0线性规划软件求解，该模型的目标函数f如下。

f=minλ1afa+minλ2bfb+minλ3cfc+minλ4dfd

(8)

式(8)中，λ1a，λ2b，λ3c，λ4d为目标函数的权系数，用于平衡4个影响因素的目标函数权重。其中，λ1a>0，λ2b>0，λ3c>0，λ4d>0，且满足λ1a+λ2b+λ3c+λ4d=1。考虑到实际问题中涉及到对多家供应商的选择，因此需要合理设置各供应商的权系数。本文采用层次分析法(AHP)对目标函数的权系数进行选取。

(2)AHP确定权重

层次分析法是一种将定性的问题定量化的实用决策方法[16]。该方法能够将复杂的问题分解成若干层次，决策者依据相对重要性函数表给出元素两两比较的重要性等级，具有可靠性高、误差小的优点。AHP法应用流程：

首先，将目标分解为多个目标或准则，按照元素相互之间的支配关系建立递阶层次结构。

其次，由专家结合实际问题，基于1-9判别标准对同一层次中的各元素针对上一层次中的某一准则判断相对重要性，构造两两比较判断矩阵。

再次，通过将判断矩阵进行归一化处理，并计算出矩阵的特征值λmax及对应的特征向量W。

最后，检验判断矩阵的随机一致性比例CR=CI/RI，其中，CI=(λmax-n)/(n-1)，n为判断矩阵阶数。通常，当CR<0.1时，即满足一致性检验。基于AHP法可得到多目标函数的有效解集，并依据有效解集选择合理的权重系数。

2.2 求解流程

基于AHP-MOLP模型相结合的供应商选择采购优化的具体步骤如下：

(1)按照各发电企业的日发电需求和物资供应商的供应量相协调构造目标函数，即：f=minλ1afa+minλ2bfb+minλ3cfc+minλ4dfd

(2)确定i家发电企业某时段t内需采购原煤的种类j，基于AHP法计算确定权系数λ1a、λ2b、λ3c、λ4d的赋权。

(3)运用Lingo线性规划软件求解出采购数量rjki(t)和目标函数f的值。

(4)基于计算出的权系数求解多目标采购优化模型，有效解集对应的方案即为由AHP-MOLP模型确定最优采购方案。

3 算例分析

3.1 基础数据

为验证本文所提方法的有效性，选取华北某地区的两家发电企业、两家电力物资供应商作为研究对象，如图1所示，对AHP法与多目标规划想结合的最优采购方案进行分析。

图1 发电企业、供应商供应区域示意图

通过项目调研等方式，收集各供应商选择计算所需的相关基础数据，如表1所示。为便于比较，假设每家供应商分别可供应两类原煤，且供货周期为[1，4]，并不考虑其它不确定因素对本算例的影响。

基于上文所述公式，给出AHP-MOLP法的最优化采购模型所构造的矩阵F为：

minF=|FA,FB,FC,FD|=

|MX,OX,LX,PX|

(9)

s.t.AX=b，X≥0

(10)

式中：Mi×j为采购成本构成的矩阵；Oi×j为不合格率构成的矩阵；Li×j与Pi×j分别为交货期和循环期构成的矩阵。

表1 各供应商的供货能力相关数据情况

3.2 优化计算与结果分析

(1)指标权重确定

建立电力物资供应商评价指标体系，如图2所示。

图2 供应商评价指标体系

运用yaahp软件构建判断矩阵，进行层次排序以及一致性检验。准则层指标判断矩阵如表2所示。

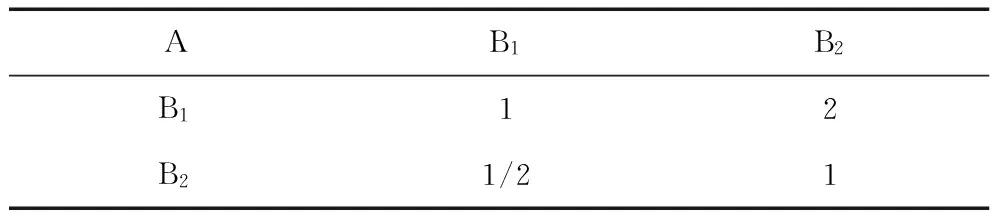
表2 准则层指标判断矩阵

经计算得W(1)=(0.667，0.333)T，λmax=1，CR=0，满足一致性检验。同理，可检验各层判断矩阵均满足一致性检验。由此计算出目标函数f的权系数分别取为λ1a=0.420，λ2b=0.218，λ3c=0.219，λ4d=0.143。

(2)算例优化结果

基于已有基础数据得到了8种不同供应情况与4个不同供货周期时段t(t∈[1，T])的采购优化计算结果，如表3所示。基于式(9)得到目标函数值F为199 780，该值为发电企业最优采购方案，即供货周期为T=2时，发电企业1每日向供应商2采购100 t原煤，不向供货商1采购原煤；发电企业2每日向供应商1采购147 t原煤，而不向供货商2采购原煤。在此基础上，分别得到M=[0.187，0.161]，O=[0.21，0.221]，L=[0.19，0.16]，P=[0.21，0.19]，A=[3，3，4，2]，b=[43，38，54，46]。

表3 采购优化计算结果

4 结论

本文针对发电企业供应链中电力物资供应商选择问题，提出了一种综合考虑产品质量、采购成本、交货期和循环期时间等影响因素的基于AHP法与多目标线性规划相结合的采购优化模型。通过算例我们发现，在给定的供应商和发电企业数量的情况下，基于本文提出的采购优化模型可以清晰地给出发电企业电力物资的最优化采购方案，算例结果也验证了所提出方法的有效性，为发电企业更好地选择物资供应商提供决策支撑。

[1]周清华，王琦.基于直觉模糊集和VIKOR的低碳供应商选择方法研究[J].科技管理研究，2017，37(10)：233-237.

[2]周清华，王琦，陈锂.基于直觉模糊集-TOPSIS的绿色供应商选择研究[J].系统科学学报，2017，25(1)：94-98.

[3]国家电网公司.物资集约化管理[M].北京：中国电力出版社，2012.

[4]LEHMANN D R，O'SHAUGHNESSY J.Difference in attribute importance for different industrial products[J].Journal of Marketing，1974，38(2)：36.

[5]JANG W，HONG H U，HAN S H，et al.Optimal supply vendor selection model for LNG plant projects using fuzzy-TOPSIS theory[J].Journal of Management in Engineering，2016，33(2)：421-424.

[6]徐杰，屈挺，聂笃宪，等.基于持续抽检的电力物资多阶段动态采购模型及系统[J].工业工程，2015，18(4)：132-139.

[7]宋斌，冷传东，沈男，等.熵模糊物元模型在电力物资供应商评价中的应用[J].物流技术，2014，33(1)：105-107.

[8]庞继芳，宋鹏.面向大型煤炭企业的物资供应商评价与选择研究[J].华东经济管理，2015，29(2)：117-122.

[9]林涛.电网物资供应商的评价和选择研究[J]. 科技与创新，2017(6)：94-95.

[10]赵惠芳，胡娟，刘军航.电力工程EPC总承包物资采购供应商选择研究[J].合肥工业大学学报(社会科学版)，2015，29(1)：10-16.

[11]商丽媛，谭清美.基于灰熵模型的应急物流供应商评价[J].统计与决策，2013(3)：45-47.

[12]娄祝坤，殷文伟，唐韵捷.供应商选择、搜寻策略与企业创新关系研究[J].软科学，2017，31(5)：56-59.

[13]董福贵，刘慧美.基于ANP/TOPSIS的燃煤供应商选择[J].现代电力，2012，29(1)：82-85.

[14]耿秀丽，叶春明.基于直觉模糊VIKOR的服务供应商评价方法[J].工业工程与管理，2014，19(3)：18-25.

[15]刘增明，陈运非，蒋海青.基于PCA-BP神经网络方法的供应商选择[J].工业工程与管理，2014，19(1)：53-57.

[16]祁莹，邓华.零售业供应链风险管理及供应商评价模型[J].东南大学学报(哲学社会科学版)，2014,16(s1)：72-74.