面向最大供电能力提升的配电网优化规划方法

李 颖， 王博天， 王 泽， 梁海峰， 刘应明， 刘建华

(1. 六盘水供电局，贵州 六盘水 553001； 2. 华北电力大学 电力工程系，河北 保定 071003)

0 引言

传统配电网规划，一般考虑负荷增长速度较快的情况，会使规划后的配电网中变压器和线路留有较大的裕度。而随着我国经济发展步入新常态，负荷的增长速度相对变缓，城市发展从中心城区开始向外辐射发展。另外，目前配电网的自动化水平和监测手段有了较大的提升，使得配电网实现拓扑重构、快速负荷转供等成为可能，此时，再像传统规划一样将容载比设计的较大或为了满足网络的安全性和可靠性，而将变压器负载率设计的比较低，会导致配电网设备裕度很大，使其不能得到充分地利用。因此，有必要研究适合当前配电网状态和发展模式的规划方法。

近年来，许多学者对配电网规划的模型和求解算法等相关问题做了大量的研究。文献[1]采用模糊技术对可靠性指标和经济型指标进行了模糊处理，使其具有同等地位，并以此建立了配电网规划的多目标模型。文献[2-3]提出了电力系统运行可靠性成本价值的评估方法，在经济性和可靠性之间建立了一个较为明确的联系，以此为基础提出了经济性和可靠性协调规划的方法。文献[4]利用非支配排序遗传算法对考虑DG和ESS的配电网多目标规划模型进行求解，取得了较好的效果。但是，上述研究主要从经济性和可靠性角度出发研究规划问题，规划过程中，尤其是针对配电网改造规划时，没有考虑充分利用原有配电网的潜力。

文献[5-8]介绍了一种在满足N-1准则下计算网络最大供电能力的模型。在该模型中，目标函数是供电能力最大和负荷分布均衡度，但是分开进行的，因此所求结果可能无法保证两个目标都能令人满意，并且在模型中对网络做了较大程度的简化，而且未考虑负荷的实际分布情况。文献[9]研究了以重复潮流法来计算配电网最大供电能力的模型，该模型可以考虑当前网络的负荷分布状态，但结果相对保守。

本文在以上研究的基础上，结合负荷分布情况，建立了配电网最大供电能力的计算模型，并以此为基础，建立基于最大供电能力的配电网线路优化规划模型，通过线路切改、加装开关和新建联络线等手段达到充分利用配电网设备潜力的目的，以此来适应负荷增长的新常态。

1 配电网最大供电能力建模

配电网的最大供电能力，即在当前实际配电网结构和负荷分布基础下满足潮流约束和容量约束的网络最大负荷供应能力[10]。基于配电网最大供电能力的定义，在考虑实际配电网的结构、负荷分布和负荷均衡的情况下，本文建立了配电网最大供电能力的计算模型，具体模型如下。

(1)目标函数

(1)

式中：PTSC为求得的配电网最大供电能力的值；Pi为负荷点i的负荷，N为负荷节点的个数。

(2)约束条件

(2)

式中：Pil、Qil为节点i的流出功率，Pi∞、Qi∞为同一条线路上i节点下游所有节点所带的负荷和，Plossi∞、Qlossi∞为i节点下游所产生的网损和；Ui为节点i的电压，Iijmax为线路i-j段容许的最大电流，Umin和Umax分别为规定的最低和最高电压；G为第m台变压器母线上各馈线的出口节点集合，Smmax为第m台变压器的最大容量。公式(2)中第3个公式代表各线段流过的容量不能超过它的最大允许电流；第4个公式代表各节点的电压要在规定范围内，第5个公式代表每台变压器流出功率不能超过它的容量。

配电网的最大供电能力值为模型中刚好有一约束不满足时配电网所供应的负荷值。求取该值最直接的方法就是重复潮流法，而且该法可以结合现有负荷分布和负荷预测的结果，计算出更符合实际情况的最大供电能力[9]。

为了提高所计算最大供电能力的准确性，本文采用了相对增长率的负荷增长模式。即设定一个基准增长率λ，然后根据负荷预测的结果，每个负荷节点处的负荷增长率为基准增长率与该负荷节点所处区域的负荷预测值的乘积。即公式(3)，

λi，i∈j=αjλ

(3)

式中：λi，i∈j为负荷节点i的增长率，i∈j为节点i属于j区域，αj为j区域的负荷预测结果。

本文采用文献[9]中确定达到配电网最大供电能力临界点的方法来求取配电网的最大供电能力。

2 配电网优化规划采用的主要措施

在原有配电网基础上对配电网进行改造规划，目标是在不降低可靠性基础上达到增大供电能力的目的。根据最大供电能力的定义，配电网限制供电能力提升的主要原因有以下3点：

(1)馈线间的负荷分布不均匀，一些重载线路过早的达到自己的临界点，限制了其它线路的负荷增长；

(2)一些线路的供电半径过长，导致末端压降过大；

(3)变压器出线过多，负荷较重。

针对以上3点原因，采用改变开关状态、新建联络开关、新建线路作为主要措施来改善配电网的网络结构，从而达到增大供电能力的目的。

2.1 改变开关性质和新建联络开关

该措施主要通过将原有联络开关改为分段开关、原有联络线路改为正常运行线路和新加联络开关或者将原有分段开关改为联络开关的办法，来实现负荷的再分配，消除配电网中的供电薄弱点。

原理图如图1所示。1号线路为负载较重的线路，且供电距离较长；2号线路为负载较轻的线路，供电距离不长；虚线线路为联络线路。经过改造后，将原有的联络线路改为2号线路的一部分，联络开关改做分段开关，将1号线路中的一段改为联络线路，并加装联络开关。在选择联络线路开关的位置时，可以优先考虑线路中原有的分段开关，这样可以节省投资。当原有的分段开关不满足要求时，则要加装联络开关。

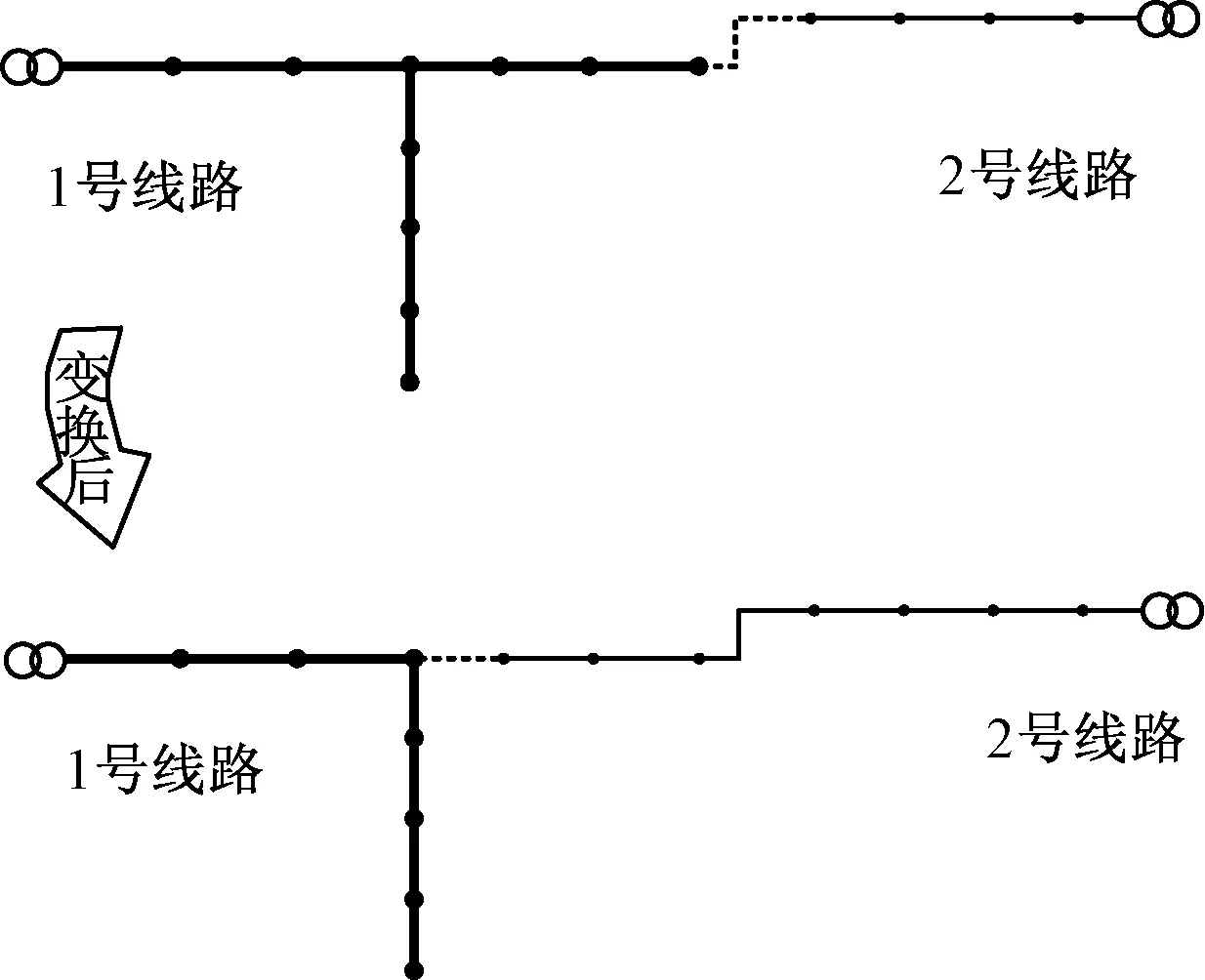
图1 改变开关性质和加装开关原理示意图

2.2 新建线路

该措施通过新建一条线路将重载线路上的部分负荷转带到轻载线路上，来达到平衡线路负载率的目的，其原理图如图2所示。1号线路为重载线路，2号线路为轻载线路，通过在两条线路之间新建一条线路，将1号线路的一个分支转带到了2号线路上，平衡了两条线路之间的负荷，有利于供电能力的提高。

图2 新建线路原理示意图

2.3 改变变压器出线

针对一些变压器存在负荷较大、出线条数较多的情况，该措施通过将出线较多的变压器上所带的馈线转移到出线较少的变压器上，或将同一变电站不同变压器间的两条负载率较低的馈线合并为一条馈线的手段来改善这种情况。

原理图如图3、图4所示。图3中，变压器1的出线较多，变压器2的出线较少。其中变压器1的某条馈线的末端接近变压器2，则可以在变压器2和这条线路末端之间新建一条线路，将馈线整体转接到变压器2上，这样既给变压器1腾出了一个间隔也平衡了变压器1、2之间的负载率。图4中，1号和2号线路都比较短，负载率也比较低，通过在节点2和节点1之间新建一段线路，并在节点1处建一个开关箱，从而将线路1和线路2合并为一条线路，在平衡了两个变压器之间负载率的同时，也腾出了一个出线间隔。

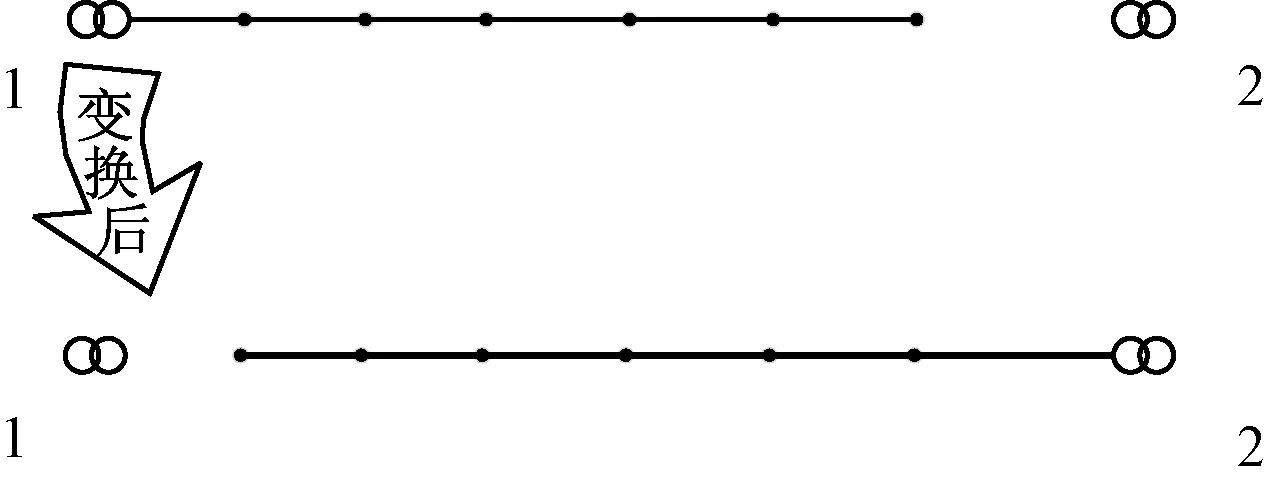
图3 改变变压器出线中转移馈线的原理示意图

图4 改变变压器出线中合并馈线的原理示意图

3 基于最大供电能力的配电网线路优化规划建模

3.1 基于最大供电能力的配电网线路优化规划模型

结合在配电网的优化规划过程中所采用的主要措施，以供电能力的大小、新建线路的总长度和加装开关的总个数为目标函数构建配电网优化规划模型，具体目标函数如下式所示。

(4)

(5)

式中，w为新建线路的条数，Ci为第i条新建线路的长度，β为将开关换算成线路的常数因子，即将新装开关的投资换算成相同投资下新建线路的长度，该值由要进行换算的开关型号和线路型号决定。Y为加装开关的总个数。

本文采用节点关系矩阵L来表示网络的优化规划状态。L为对称的0-1矩阵，为了避免网络复杂化，每行或每列的元素之和不能超过1，即每个节点只会与一个其它节点相连。若L中的某个元素为1，该元素所处位置的行坐标和列坐标所代表的两个节点a和b之间新建线路。其具体情况有以下几种：

(1)若两个节点不包含主变压器母线节点，且两个节点之间之前并没有线路。若a节点为重载线路上的节点，则将a及其下游节点全部接到b节点上。

(2)若两个节点不包含主变压器母线节点，且两个节点之间已存在线路。若a节点为重载线路上的非末端节点，则将a及其下游节点全部接到b节点上，即把联络开关改做分段开关。

(3)若两个节点不包含主变压器母线节点，且两个节点之间已存在线路。若a节点为重载线路上的末端节点，则找一个合适的位置设为联络开关，使得两条线路的负载率相近，优先利用原有分段开关，如无合适的分段开关可用则新加开关。

(4)若节点中有一个为主变压器母线节点，设a节点为主变压器母线节点，则以b节点为出口节点，将整条线路转移到a节点变压器上。

(5)若两个节点中，存在一个节点为紧邻出口的节点a，且b节点线路的负载也不重，则将a节点及其下游全部转到b节点上，腾出一个出线间隔。

模型的约束条件为功率约束、电压约束、可靠性约束和变压器均衡度约束。

3.2 优化规划模型的求解

上述面向最大供电能力提升的配电网线路优化规划模型为一个多目标的优化问题，求解该问题较为有效的一个方法为非支配排序遗传算法——搜索Pareto前沿的有效方法[11-13]。

算法中的适应度函数由目标函数和约束违限惩罚函数构成。其构成如下：

(6)

式中：F1(xi)和F2(xi)分别为最大供电能力和经济投资的适应度函数；f1(xi)和f2(xi)分别为最大供电能力的值和经济投资的值，v(xi)为约束条件的总违限量[14]，α1和α2分别为两个目标函数的惩罚因子，该值为大于1的常数，其具体大小则根据适应度函数的值来确定。

若两个个体xa和xb满足

(7)

则xa支配xb，否则互不支配。种群中所有不被其它任何个体支配的个体构成Pareto解集。最后的决策方案则在该解集中挑选。

4 算例分析

本节首先采用IEEE 42节点的配电网算例验证本文模型和方法的实用性和合理性，然后对六盘水市中心城区配电网进行了优化规划。

4.1 42节点配电网算例分析

该算例的网络拓扑结构如图5所示，其中节点1、15、29为电源节点，一共9回10 kV馈线，联络线路有5条。联络线路指联络开关所在的线路，即图中的虚线。

图5 42 节点配电网网络拓扑图

图6 所有个体的分布图

取种群规模为100，迭代次数为50，交叉概率比较后取为0.9，变异概率取为0.1。按照所提方法对该算例进行优化得到以下结果。图6和图7分别为种群中所有个体的分布图和Pareto非支配解的分布图。表1、表2分别为初始网络和优化后各方案的各项指标，表中可靠性1为初始负荷状态下的可靠性，可靠性2为当负荷达到最大供电能力状况下的可靠性，初始负荷和最大供电能力的单位均为MVA，新建线路长度的单位为km。

图7 Pareto非支配解的分布图

初始负荷/MVA可靠性1/%最大供电能力/MVA可靠性2/%网损率/%变压器负载均衡度28.402899.762339.157199.73233.33320.3199

表2 优化后网络的各项指标

对比优化后的结果可得，本文所提方法和模型可以有效提高配电网的供电能力，并且变压器负载均衡度和线损率也有提高。本文选定方案5，对网络拓扑结构的改变进行分析。

图8 方案5的网络拓扑结构

由图8可得6和11节点间的联络开关移到了11和3节点之间，39和41节点之间的联络开关移到了31和39节点之间，7和21节点之间的联络开关移到了19和21节点之间，并在14和37节点之间新建线路，并将36和37节点之间的线路改为联络线路。

由于1-2这条馈线所带负荷较少，1-3和15-16两条馈线带的负荷较重，因此这两条线路分别转移了一部分负荷到1-2馈线上。29-31馈线所带的负荷比较重，故转移了部分负荷到29-32和1-4馈线。在转移的过程中，优先利用了配电网原有的线路。为了减轻29-31的负荷，易于转移的有37和38节点，虽然38节点和15-17馈线上的23节点之间存在联络线路，但是15-17馈线负荷也较重，不利于转移，因此，在14和37节点间新建了线路。通过这些措施，实现了负荷在线路间的平衡，网损率和变压器负载率均衡度均得到了提升。

综上，本文所提方法可以在不对现有网络进行大范围变动并且有效反应区域负荷增长率的前提下给出可行的优化规划方案，有效地消除了配电网中的供电瓶颈，从而提高了配电网的供电能力。由于以消除配电网中的重载线路为手段来提高供电能力，在提升供电能力的同时，有效降低了变压器间负载率的差值，使得负荷分布更均衡，从而在一定程度上降低了网损率。

4.2 对10kV实际电网的优化规划

以贵州某市中心城区的一个片区为例，该片区包含5个110/10kV变电站、一个220/110/10kV变电站和5个开闭所，功率因数稳定在0.9左右，共包含97条出线。

按本文方法对该片区进行优化规划，结果如表3所示。

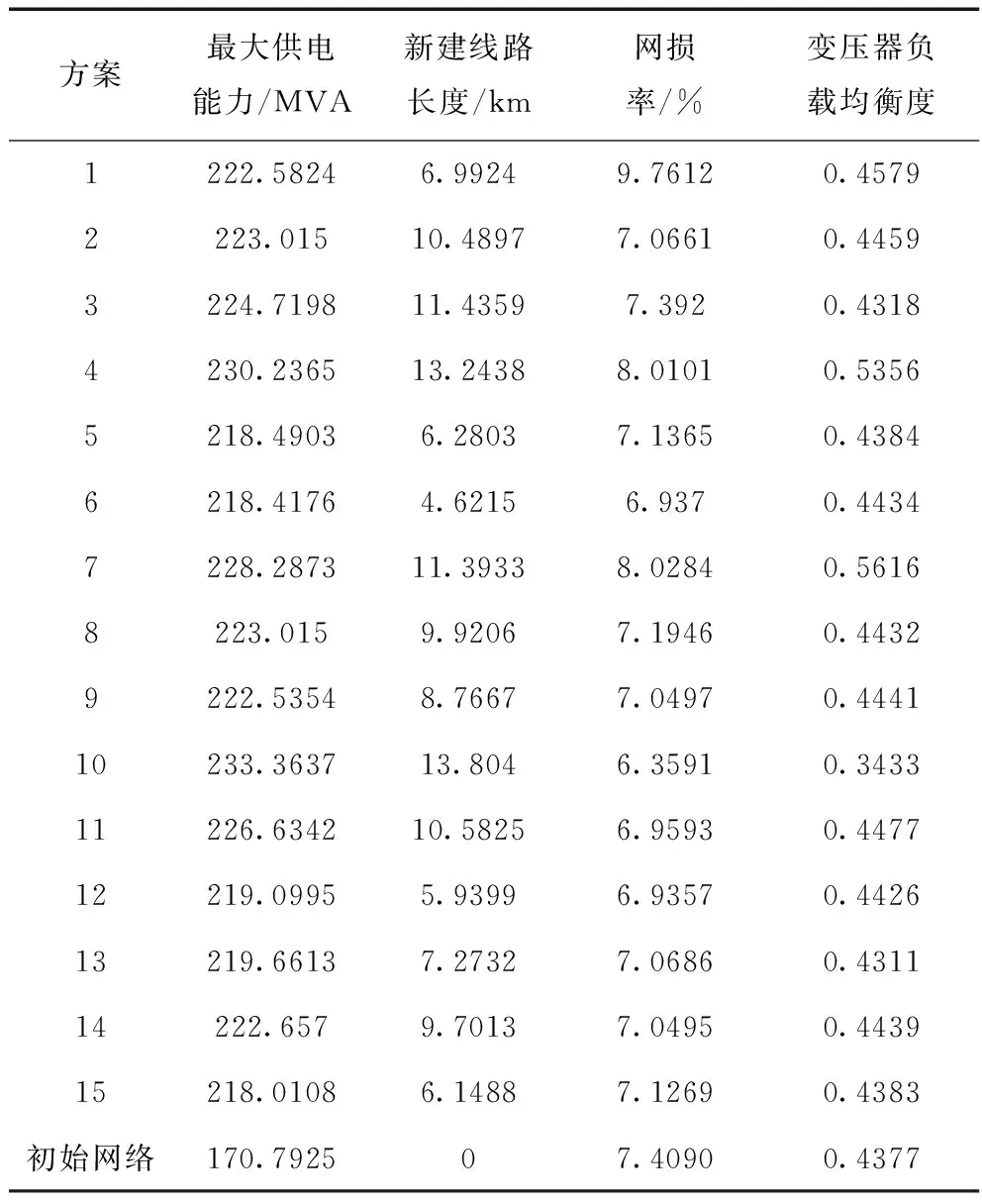
表3 算例2的优化结果

原始网络的负荷分布不太均匀，重载线路甚至超载线路较多，严重限制了供电能力的提升。在优化方案中，通过转移重载和超载线路上的负荷到轻载线路上，改善网络的负荷分布，从而使供电能力得到了显著提高，其中方案10的经济性指标虽然较差，但其供电能力、网损率和变压器负载均衡度这3个指标均得到了较大幅度改善，本文选定方案10作为最终优化规划方案。由于实际配电网中变压器间出线条数并不一致，线路间负荷的均衡并未使变压器负载均衡度得到较好改善，有的方案该项指标甚至没有得到改善。但是，该指标在模型中是作为约束条件存在的，满足约束条件即可。可见，本文方法可以较好的适用于10 kV配电网。

5 结论

针对面向最大供电能力提升的配电网优化规划问题，从计算最大供电能力的原理入手，分析了限制供电能力提升的主要原因，以此为根据提出了优化规划的主要手段，并在此基础上建立多目标的优化规划模型，得到如下结论：

(1)实际电网中，存在的重载线路或者供电半径较长的线路，因其载流量限制或者电压限制而成为限制配电网供电能力提升的主要瓶颈，而通过转移转移瓶颈线路的部分负荷和部分线路，可以有效消除供电瓶颈，从而提升配电网供电能力。

(2)充分利用了配电网的原有设备，实现了以较小的成本来改善配电网拓扑结构的目的，为配电网规划提供了实际而科学的指导意义。但是，实际配电网的结构比较复杂，需要考虑的因素众多，因此本文所提模型还需进一步完善。

[1]王赛一，王成山．基于多目标模型的城市中压配电网络规划[J]．中国电力，2006，39(11)：46-50．

[2]何剑，程林，孙元章．电力系统运行可靠性成本价值评估[J]．电力系统自动化，2009，33(2):5-9．

[3]程林，焦岗，田浩.可靠性与经济性相协调的配电网规划方法[J].电网技术，2010,34(11):106-110.

[4]盛四清，刘梦.一种同时考虑DG和ESS选址定容的主动配电网规划方法[J].电力科学与工程，2015，31(10):21-26.

[5]肖峻，谷文卓，郭晓丹，等. 配电系统供电能力模型[J]. 电力系统自动化，2011，35(24)：47-52.

[6]肖峻,谷文卓,贡晓旭,等. 基于馈线互联关系的配电网最大供电能力模型[J]. 电力系统自动化，2013，37(17):72-77.

[7]XIAO J，LI F，GU W Z，et al．Total supply capability and its extended indices for distribution systems：definition，model calculation and applications[J]．IET Generation，Transmission & Distribution，2011，5(8)：869-876．

[8]肖峻,祖国强,李晓辉,等. 基于最大供电能力的配电网馈线联络建设次序规划方法[J]. 电力系统自动化，2014，38(11):49-55.

[9]朱静,高亚静,刘建鹏,等. 主动配电网供电能力实时评估方法[J]. 中国电力，2015，48(12)：96-102.

[10]荆朝霞,王宏益,江昌旭. 考虑负荷均衡的220kV电网供电能力多目标优化[J]. 电网技术，2017，41(5):1619-1628.

[11]DEB K，PRATAP A，AGARWAL S，et al．A fast and elitist multi-objective genetic algorithm：NSGA-II[J]．IEEE Transactions on Evolutionary Computation，2002，6(2)：182-197．

[12]马燕峰,范振亚,刘伟东,等. 考虑碳权交易和风荷预测误差随机性的环境经济调度[J]. 电网技术，2016，40(2):412-418.

[13]董萍,徐良德,刘明波. 多站点无功补偿装置的多目标协调控制[J]. 中国电机工程学报，2014，34(4):587-595.

[14]李力,李剑辉,高超,等. 包括供电瓶颈识别的电力系统供电能力评估[J]. 电力系统及其自动化学报，2013，25(3):43-49.