基于集合经验模态分解的组合风速预测方法

雷 爽， 王鹏卉， 张亚刚

(新能源电力系统国家重点实验室(华北电力大学)，河北 保定 071003)

0 引言

随着煤、天然气等传统化石能源的储量日趋减少，各国开始纷纷致力于新能源的研发。风能作为新能源的一种，具有清洁、无污染、储量丰富等优点被广泛地发展应用。但是，由于风速具有很强的波动性、随机性和间歇性，大规模的风电在接入电网时会对电网的安全性和稳定性带来严峻的挑战，也因此带来了大量的弃风现象[1]。精确的风速预测可以对电网调度提供有效的调度支持，对风电的大规模应用具有重大意义。

风速预测方法一般可分为基于历史数据的预测方法和基于数值天气预报数据的预测方法。基于历史数据的风速预测方法主要包括持续法、时间序列法、神经网络法、卡尔曼滤波法等[2]。

持续法是直接将某一时刻的风速值直接作为下一点的预测值，这种方法虽然简单、高效，但是不能体现风速的变化[3]。时间序列方法主要应用自回归移动平均模型(Auto Regressive and Moving Average，ARMA)，自回归差分移动平均模型(Auto Regressive Integrated Moving Average，ARIMA)和广义自回归条件异方差模型(Generalized Auto Regressive Conditionally Heteroscedasty，GARCH)。丁腾，冯冬涵等人基于ARIMA模型和GARCH模型，对风速序列建立了ARIMA-GARCH模型，并利用模糊理论、风速分布特性等相关分析方法对预测进行修正，得到了较好的预测结果[4]。但是，时间序列预测方法往往具有一定的滞后性，难以对风速的突变迅速反应且需要大量数据进行模型的拟合[5]。神经网络，支持向量机等方法是基于风速的数值变化规律对风速进行预测，仅需历史数据即可建立模型，但存在训练集难以选择，模型易出现过拟合现象等缺点[6-8]。卡尔曼滤波法只需要少量历史数据就可利用线性系统状态方程得到预测值[9]，但其状态方程与测量方程的建立较为困难。

灰色理论自1982年提出以来，受到了国内外各界学者的广泛关注与研究。由于在建模过程中需要的数据量小，且不需要对其它统计量进行计算等优点，灰色预测模型在工业，科技，经济等各大领域被广泛应用[10-12]。在预测的研究中常用的是一阶一变量模型，即GM(1,1)模型，但GM(1,1)模型只有在对单调时间序列进行预测时才有较好的效果。为了提高适应性，本文采用GM(2,1)模型，即二阶一变量灰色模型进行预测。

本文基于集合经验模态分解与灰色理论方法建立了一种风速预测模型，并利用小波分解，神经网络等方法对模型做了改进，并做了实例分析与多模型预测效果的对比。

1 集合经验模态分解

经验模态分解(Empirical Mode Decomposition, EMD)是一种针对非线性非平稳信号的自适应处理方法，利用经验模态分解可以有效提高组合预测方法的预测精度[13]。如果一个信号曲线的极值点个数和过零点个数差值小于等于1且两条包络线的均值为零，则称其为一个本征模函数。任何一个信号都能够被分解为若干个本征模函数(IMF)。经验模态分解就是通过对本征模函数不断进行识别与提取，从而将非平稳、非线性的复杂信号分解为多个简单信号。

经典的经验模态分解方法存在一定的模式混淆现象，而集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)通过多次添加白噪声进行分解再求均值去噪的方法有效抑制了模态混淆现象。对风速序列进行集合经验模态分解，可以有效地降低其数据复杂程度[14]。类似的信号分解方法还有小波分解(Wavelet Decomposition,WD)，即一种将时域信号转化到频域进行分析，再还原到时域的信号分解的方法，小波分解可以有效挖掘序列的波动特性，在本文中也有应用。

集合经验模态分解的步骤如下：

首先对原始序列v(t)多次添加幅值相同且均值都为0的高斯白噪声ni(t)(i=1,2,…,k)，其中，k为添加不同白噪声的次数。添加不同白噪声的原始序列生成的新序列为

vi(t)=v(t)+ni(t)

(1)

之后对新生成的序列分别进行经验模态分解。

对于任意的新生成序列，为获取本征模函数，首先找到序列vi(t)的所有极大值与极小值，通过三次样条插值方法构造出原始序列的两条包络线，分别记为yi(t)以及zi(t)，计算上下包络线所有数据的均值，即可得到平均包络线为

(2)

用原始序列减去平均包络线，得到一个新的差值序列为

di1(t)=vi(t)-mi(t)

(3)

式中：若di1(t)不是本征模函数，则分解停止；若di1(t)是一个本征模函数，则将mi(t)当作新的vi(t)，再次对mi(t)求平均包络线，计算差值序列。重复上述过程直至获得l个本征模函数dij(t)(j=1,2,…,l)。对于非平稳的信号，经过EMD分解得到的残余波形往往有一定的趋势，称为趋势项，可以表征序列的总体趋势，记为ri(t)。

最后，对k个新序列vi(t)的经验模态分解结果计算均值可得：

(4)

(5)

式中：imfj(t)(j=1,2,…l)为原始序列经集合经验模态分解得到的l个本征模函数；r(t)为趋势项。

2 GM(2,1)模型

灰色预测能够通过相对少量的信息揭示难以直接观察到的灰色系统内部的发展、变化过程。现今大部分对灰色预测模型的研究都针对于GM(1,1)模型。由于只能表示单一的指数形式，GM(1,1)模型通常用于单调时间序列的预测，难以体现数据的波动性。

GM(2,1)模型是指二阶一变量灰色预测模型，下面简述其原理。

记原始序列为

V(0)={v(0)(1),v(0)(2),…,v(0)(n)}

(6)

对原始序列进行累加，可得累加生成序列为

V(1)={v(1)(1),v(1)(2),…,v(1)(n)}

(7)

式中：上标“0”和 “1”分别表示原始序列与一次累加生成序列。其中，

我们假设经一次累加得到的生成数v(1)满足二阶常微分方程：

(9)

式中：a1、a2和a3为模型的参数，则将该方程称为白化微分方程。

构造v(1)的紧邻均值序列Z(1)：

Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))

(10)

近邻均值序列即序列相邻数均值构成的序列，即

z(1)(k)=0.5v(1)(k)+0.5v(1)(k-1)

(11)

式中：k=2,3,…,n。

为了对参数进行估计，令

(12)

(13)

(14)

利用参数的估计值即可对二阶白化微分方程进行求解得到预测模型。

值得注意的是，在求解一般微分方程的过程中，一般通过代入原始数据点的方式求解参数C1和C2，但这种方法相当于默认新建立的灰色模型曲线会通过该点。本文采用最小二乘方法对C1和C2进行求解，将预测值与实际值的残差平方和最小为目标进行求解。

最后，对白化方程的解进行累减还原即可得到预测结果：

V(0)(t)=V(1)(t)-V(1)(t-1)

(15)

3 组合模型实现

首先，将收集到的风速序列进行集合经验模态分解，得到数个本征模函数与一个趋势项。对于低频IMF与序列趋势项，直接利用GM(2,1)模型预测，并将结果组合，得到趋势预测结果。对于高频IMF，本文利用小波分析的方法从频域的角度再次进行分解，以获得高频本征模函数中的相对低频趋势分量。利用GM(2,1)模型对低频部分进行预测，其结果再与趋势预测结果加和，得到更为精确的初步预测结果。最后，采用RBF神经网络，对小波分解得到的高频波动项进行预测，并与初步预测结果加和，得到最终预测结果。

组合模型的实现过程如图1所示。

图1 预测模型流程图

对于经EEMD分解得到的低频本征模函数，其均值接近于零，从整体来看没有明显的趋势性，但从局部分析的角度看，在一定的时段长度内仍然具有一定的趋势性。因此，采用GM(2,1)模型对低频本征模函数与分解得到的趋势项进行预测，预测结果之和作为趋势预测结果。高频本征模函数仍具有较强的随机性和波动性，单调区间短，因此不适合采用GM(2,1)模型预测。为进一步提高预测精度，本文对高频本征模函数进行小波分解，将高频本征模函数分解为低频趋势分量与高频扰动。所得的低频趋势分量代表了高频本征模函数的变化趋势，利用GM(2,1)模型对低频趋势分量进行预测，并与趋势预测结果加和得到初步预测结果。

上述预测方法将小波分解得到的高频分量当作扰动，而风本身就是一种随机扰动，因此，为了获得更高的预测精度，对高频细节离散信号同样进行了分析。但是灰色模型对于强波动性数据的预测效果较差，往往不能充分体现序列的波动特性。选用RBF神经网络对高频分量进行预测，理由如下：

(1)小波分解是一种频域的分解方法，经小波分解得到的分量，其波动往往具有较强的规律性；

(2)神经网络方法先通过一定量的训练形成网络，再依据建立好的网络输入新的数据进行预测，其训练集的规律性越强，曲线变化特点越一致，预测效果越好。

4 实例分析

选择西班牙SOTAVENTO风电场2016年4月的数据进行实例分析，风速数据总数为4 320个，风速数据间隔为10min。风速数据如图2所示。

图2 风速数据

通过对数据进行统计分析，可得到如下统计量，如表1所示。

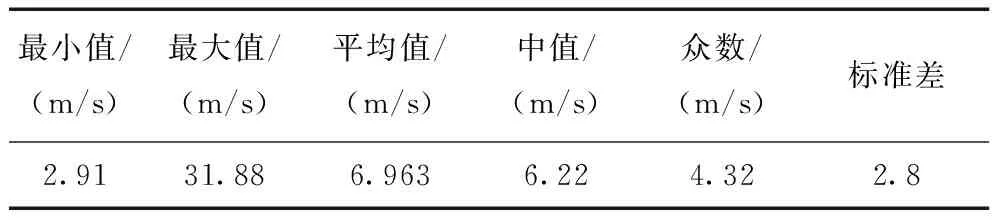
表1 风速数据统计量

从图2可以看出，风速具有极强的波动性和随机性。在一定的总体变化趋势下反复波动、高速变化是一组风速序列的常态。从表1可看出风速数据具有很大的极差与标准差。原始风速序列是复杂的非线性、非平稳序列，对其进行集合经验模态分解可以有效降低其复杂程度，将原始风速序列分解成便于进行预测的简单序列。

多次从总样本中选取3天,累计432个数据进行预测分析，其中前309个数据作为训练集，后123个数据作为测试样本。进行集合经验模态分解时,分别对原始风速序列添加100组高斯白噪声，白噪声序列的标准离差则设为0.1。

根据上述建模预测过程，对所选样本区间数据分别进行建模预测，预测结果如图3所示。

从图3可以看出，GM(2,1)模型比较适用于非单调、有一定波动的数据的预测，但是同一般的时间序列预测方法一样，具有一定的滞后性，对数据波动趋势的反映往往落后真实值一步。并且，由于灰色预测方法的指数形式，在数据波动性大的情况下容易被少数极端变化的原始序列影响，从而得出与真实值相差很远的极端错误预测。

初步预测结果即分解得到的低频序列经灰色模型处理得到的预测结果，从各预测方法结果的

(a) 4月1日-4月3日预测结果对比

(b) 4月6日-4月8日预测结果对比

(c) 4月12日-4月15日预测结果对比

(d) 4月28日-4月30日预测结果对比图3 模型预测结果

对比图中可以看出，初步预测结果很好地反映了风速序列的变化趋势，并且不再出现极端错误预测的情况。这说明对原始序列进行集合经验模态分解，利用较为平稳，波动性小的分量序列进行预测，可以有效避免灰色预测方法的弊端。但同样可见，初步预测结果是一条相对平滑的曲线，不具有原始风速序列曲线剧烈的波动性。如图3所示初步预测结果与原始风速序列有相同的变化趋势，但基本没有与样本曲线极值点重合的情况；从图3(d)可见，在原始风速没有明显总体趋势的时段内，初步预测结果接近一条平稳曲线。这说明，由于预测时将原始序列的高频分量当作随机扰动，尽管初步预测结果能够很好地反映风速序列的总体变化趋势，但难以体现趋势之外的波动变化，造成预测精度较低。

可以看出，对风速进行集合经验模态分解后，直接建立RBF神经网络预测模型不能得到良好的预测效果。这说明由于风速具有很强的随机性和间歇性，其变化规律的复杂性难以通过一次集合经验模态分解而消除。

在初步预测结果的基础上，利用RBF神经网络对高频分量进行预测并将其作为扰动的预测与初步预测结果进行加和，即得到最终预测结果。从图3可以看出，最终预测结果无滞后现象，与样本曲线非常接近，能够同时反映风速序列总体变化趋势和细节波动。这说明，对原始风速序列依次进行集合经验模态分解和小波分解可以得到具有很强规律性的高频分量，而这些高频分量非常适合采用RBF神经网络进行预测。

采用平均绝对误差(MAE)和平均绝对百分误差(MAPE)对各模型进行评价和对比，对比模型分别为EEMD-RBF预测模型和GM(2,1)模型。其结果如表2所示。

表2 预测误差对比

文中提出的组合预测模型平均绝对误差均小于0.2 m/s，平均相对误差分别为1.582%、1.459%、1.74%和2.35%，在4次预测中，两种误差的平均值分别为0.148 m/s和1.78%，预测精度良好且较为稳定。在前3个时段的预测误差指标中，EEMD-RBF组合模型的平均相对误差均在3%～4%之间，预测精度可以接受，但在4月28日到4月30日的风速预测中，平均相对误差为6.491%，效果较差。在4次预测中，GM(2,1)模型都拥有最大的平均绝对误差和平均相对误差，且平均相对误差均大于7%，在4月28日到4月30日的风速预测中甚至达到了11.36%。

综上，与EEMD-RBF模型以及GM(2,1)模型相比，本文提出的模型在预测精度与稳定性上都有明显地提高。

5 结论

本文提出的组合灰色风速预测模型克服了单一神经网络、灰色模型以及时间序列等预测方法预测结果滞后的缺点，充分利用集合经验模态分解方法、GM(2,1)模型以及RBF神经网络的优点将他们有机地结合在一起，可以有效减少风速波动性的影响，显著提高了风速预测精度，具有广阔的实际应用前景。

[1]何世恩, 郑伟, 智勇,等. 大规模集群风电接入电网电能质量问题探讨[J]. 电力系统保护与控制, 2013，41(2):39-44.

[2]汪小明, 肖猛, 杨楠,等. 基于小波分解和极限学习机的短期风速组合预测研究[J]. 可再生能源, 2015, 33(8):1159-1163.

[3]高爽, 冬雷, 高阳,等. 基于粗糙集理论的中长期风速预测[J]. 中国电机工程学报, 2012, 32(1):32-37.

[4]丁藤，冯冬涵，林晓凡，等. 基于修正后ARIMA-GARCH模型的超短期风速预测[J]. 电网技术. 2017,41(6): 1808-1814.

[5]张江昆，常太华，孟洪民，等. 基于ARIMA与Elman神经网络的短期风速组合预测方法[J]. 电子世界. 2013,22(18): 79-80.

[6]石亚欣. 基于时间序列的WD LS SVM的风速周期预测模型研究[J]. 电力科学与工程, 2014,30(2):41-45.

[7]宋菁华，杨春节，周哲，等. 改进型EMD-Elman神经网络在铁水硅含量预测中的应用[J]. 化工学报. 2016, 67(3): 729-735.

[8]薛翔, 赵冬梅, 王金奕,等. 基于ARIMA与双层BP神经网络相结合的风电功率预测方法[J]. 电力科学与工程, 2012, 28(12):50-55.

[9]杨明莉，刘三明，王致杰，等. 卡尔曼小波神经网络风速预测[J]. 电力系统及其自动化学报. 2015,27(12): 42-46.

[10]党耀国，王俊杰，康文芳. 灰色预测技术研究进展综述[J]. 上海电机学院学报. 2015,18(1): 1-7.

[11]朱彦鹏，江腾，朱鋆川. 山区机场高填方边坡施工期沉降的灰色模型预测[J]. 甘肃科学学报. 2016,28(1): 88-92.

[12]王新胜，左伟芹，周成涛，等. 基于非齐次指数函数灰色模型的隧道围岩变形预测[J]. 现代隧道技术. 2017,54(1): 105-109.

[13]WANG J, ZHANG W, LI Y, et al. Forecasting wind speed using empirical mode decomposition and Elman neural network[J]. Applied Soft Computing. 2014, 23(5): 452-459.

[14]祝晓燕, 张金会, 付士鹏,等. 基于集合经验模态分解和支持向量机的短期风速预测模型[J]. 华北电力大学学报(自然科学版), 2013, 40(5):60-64.