用于提升风电场短期功率预测准确率的储能系统出力控制策略
2018-02-05王开让董建明
李 娜,白 恺,柳 玉,王开让,巩 宇,董建明
用于提升风电场短期功率预测准确率的储能系统出力控制策略
李 娜1,2,白 恺1,2,柳 玉1,2,王开让1,2,巩 宇1,2,董建明1,2
(1国家电网公司风光储联合发电运行技术实验室,北京 100045;2国网冀北电力有限公司电力科学研究院,北京 10045)
目前对于储能系统应用于平抑新能源发电的波动性、移峰填谷等场景的控制策略已有文献研究,但对于风功率预测准确率影响风电场效益的机制下储能系统应用的可行性尚未见研究。本文提出了一种以减小风电场短期功率预测偏差为目标的储能系统出力控制策略,控制策略以风电场实时出力数据(秒级)为数据源,采用线性外推加以移动平均优化的方法预测下一时刻风电场出力,通过比较风电场短期功率预测值与实时预测值,计算储能系统期望出力,并根据储能系统不同SOC区间内的出力能力进行约束,输出储能系统出力指令,最后进行了仿真验证。结果表明,本文提出的储能系统出力控制策略,能够使风电场通过配置储能系统,减少短期功率预测准确度考核,对风电场的精益化运行具有指导意义。
储能系统; 风电场短期功率预测; 准确率; 荷电状态(SOC)
在全球风光发电高速发展的大背景下,受限于储能投资巨大,国内外大容量储能应用主要停留在示范阶段,储能系统的应用场景也在探索中[1-2]。目前已有的储能应用分为储能单独使用和与其它发电单元相配合使用两种[3],作为独立单元应用时,可用于平抑负荷峰值、削峰填谷等,参与频率调节,提供黑启动功能,也可用于用户的能量需求峰值时段转移,从而利用电力市场的差额电价减少用户支出;可提高电能质量、增强供电可靠性等。储能与其它发电单元相配合使用时,一是针对风、光等可再生能源发电的间歇性和不可预测性,平滑可再生能源发电单元的功率输出曲线;二是可缓解风、光发电的预测偏差所带来的影响,根据预测情况储能配合辅助输出,可提高单元输出的可靠度。
国内外对储能系统在不同应用场景下的控制策略已有研究,文献[4]从风电波动率限制条件出发,将储能系统的荷电状态(SOC)和风电功率波动率作为约束条件,采用移动平均算法实现风电功率的平滑控制,通过调节移动平均控制器的平滑循环次数与权值达到风电功率平滑的目的。文献[5]提出了一种以平滑风电出力为目标的储能系统出力控制策略,储能系统SOC值作为一阶卡尔曼滤波算法的反馈,使储能系统出力能够满足SOC约束和风电波动率出力要求。文献[6]研究了微网系统中的储能变流器控制策略,使得储能系统出力、响应时间等方面满足平抑风电波动的要求。文献[7]建立了电池储能系统和风力发电系统的整体动态数学模型,采用风电场低压侧母线有功功率和电压作为控制信号,仿真结果表明:电池储能系统可以很好地改善风电场的电能质量和稳定性。文献[8]提出了基于低通滤波原理的风电功率波动平抑控制策略,利用储能系统补偿风电功率中的高频分量,构建了评价风电功率波动平抑效能的指标,但未考虑电池荷电状态[9-11]。基于大气稳定性这一属性,使用风电出力和数值天气预报历史数据作为输入,应用各种数学算法,推算下一时刻(小时级)风电出力。
上述文献中储能系统的控制目标均为平滑风电的出力波动或提高新能源发电的电能质量,基于日前风功率预测定价的电力市场机制下储能应用的可行性尚未见研究。在我国,为了提高风电消纳水平,电力调度部门通常对风电场短期功率预测准确率进行考核,在上述背景下,本文以某风电场全年短期功率预测数据和实际出力数据为基础,研究通过控制储能系统功率减少风电场短期预测偏差的可行性。提出基于线性外推法和移动平均法的储能系统出力期望值预测方法,通过风电场实时出力修正控制指令,通过计算下发储能系统出力功率指令。最后通过仿真验证了控制策略能够提高风电场短期功率的预测准确率。
1 控制策略设计方案
目前风电场短期功率预测准确率的影响因素主要是数值天气预报的准确性及预测算法的精度,本文假设该算法能够达到的预测准确率为固定参数,在此基础上,通过加配储能装置进一步提高预测准确率。其中风电场短期功率预测准确率的计算方法参考国家电网企业标准《风电场功率预测预报管理暂行办法》,其中对风电场输出功率预测的考核指标为日风电功率预测准确率,计算方法见式(1)

储能系统控制策略的总体思路如图1所示,控制目标是提高风电场短期功率预测准确率,输入为风电场实际出力和风电场短期功率预测曲线,计算方法为线性外推法和移动平均法,计算过程为预测下一时刻(秒级)风电出力功率,与短期功率预测值做差值,得出储能系统出力期望值,约束条件为储能系统剩余容量、能量和SOC运行区间的限制,最终输出储能系统出力指令。
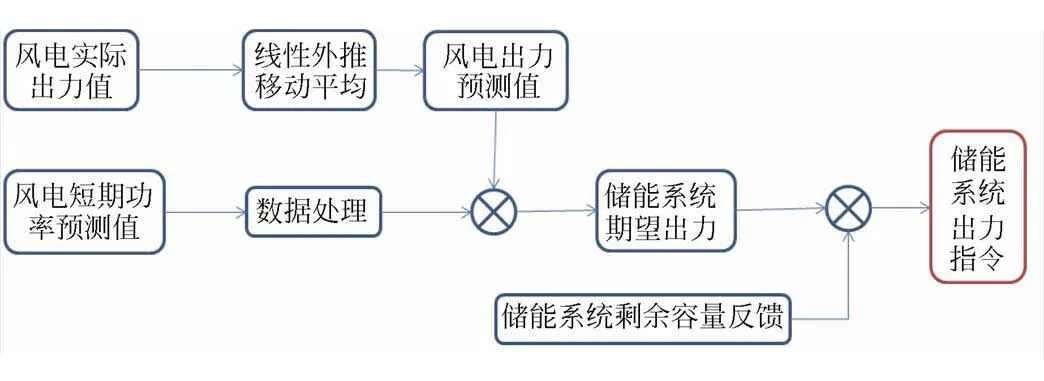
图1 储能单元出力控制策略
在总体思路中,关键的步骤一是准确计算储能系统期望出力,二是根据储能系统当前状态对期望出力进行边界条件约束。
2 控制策略计算方法
2.1 储能系统出力期望值计算
储能系统出力期望值计算的第一步是依据风电场实时出力历史值预测下一时刻风电出力。本文利用线性外推法预测,并使用移动平滑法进行优化。
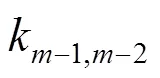
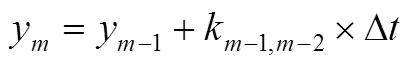
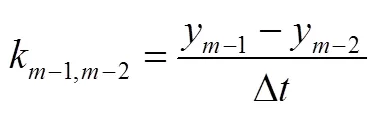

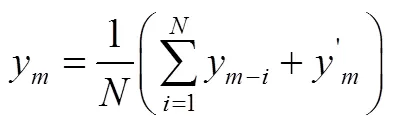
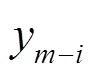
移动平均窗口长度的选择过长或者过短均会影响计算的准确度,本文在移动平均窗口长度选择研究上,采用统计的方法,如表1所示,选择不同长度的移动平均窗口长度,计算多天的预测数据。结果证明当滑动窗口长度=3时,预测精度均高于其它取值时的预测精度,因此选择=3作为移动平均窗口。

表1 移动平均窗口长度对准确率的影响
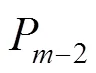

图2 储能系统期望值输出模块流程图
2.2 储能系统出力指令修正
在考虑储能系统出力约束时,参考目前国内某在运营储能电站运行参数的设定方法,将SOC区间分为最大功率出力区间、额定功率出力区间及不安全出力区间。在各个区间中考虑储能系统额定功率、额定容量及SOC运行范围。
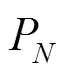

图3 储能系统出力功率限制曲线
设计储能系统出力能力反馈模块流程图如图4所示,依据储能系统当前SOC状态,判断储能系统是否在SOC安全运行区间10%~90%,若运行在安全区域则再次判断是否在允许1.5倍额定功率出力的运行区间,然后根据所在区间,判断剩余容量是否满足储能期望出力值,如满足则按期望值出力,如不满足则按照剩余容量出力。如果超出安全工作范围,则储能出力为0,等待下一充放电转换时刻再次进行判断。在SOC边界区域,可能出现剩余容量不能够维持下一秒以额定功率出力,需计算剩余容量能否满足储能系统以期望值持续出力,如果可以按照计算值进行指令下发,如果不可以,按照可用容量值进行指令下发。

图4 k时刻储能系统输出功率计算流程图
3 算例分析
为了验证课题研究的储能系统出力控制策略,选择冀北地区A风电场作为分析对象,容量为100 MW。参考已有风储电站配比,配置锂电池储能系统14 MW/63 MW·h,储能系统SOC初始状态设置为50%。在A风电场全年风功率预测数据及实际出力数据中,选择短期功率预测准确率覆盖70%、80%、90%左右3种情况,相应出力曲线采用2016年1月2日、7月9日、9月10日的实测功率和预测功率数据。
(1)数据样本1(2016年1月2日)
图5为A风电场1月2日风电机组实时出力曲线和日前发电计划曲线,风功率准确率81.33%,合格率86.94%,以此数据为样本,应用课题研究的储能单元控制策略。
首先验证使用线性外推法与移动平滑法预测风电场出力的预测精度。图6是以当天实测曲线历史值作为输入,预测的下一时刻的风电出力。可见,线性外推法与移动平滑法综合应用的预测曲线接近风电场实测功率曲线,预测误差最大不超过8%,预测精度满足使用要求。

图5 2016年1月2日实测功率曲线和预测功率曲线

图6 2016年1月2日实测曲线与算法输出曲线对比
图7为配置储能后对预测功率曲线的跟踪效果,可以看出控制储能系统跟踪风电预测曲线后,风储联合出力相比风电实际出力更加靠近短期功率预测曲线。而在储能系统出力受限时,风储联合出力曲线与风电实际出力曲线重合。

图7 2016年1月2日储能系统控制策略跟踪效果图
此时储能系统出力期望值与实际出力曲线如图8所示,储能系统SOC变化曲线如图9所示。

图8 2016年1月2日储能系统实际出力曲线与期望曲线

图9 2016年1月2日储能系统SOC变化曲线
表2分别是未使用储能进行跟踪计划发电及采用储能系统控制策略得到的风电场输出功率的准确率和合格率。

表2 数据样本1计算结果
(2)数据样本2(2016年7月9日)
图10为7月9日风电场日前预测曲线和实测曲线,风功率预测准确率为71.11%,合格率为63.82%。采用本文研究的储能系统控制策略进行预测跟踪,效果见图11、图12和表3。

图10 2016年7月9日风电场日前预测曲线和实测曲线
由图1和图12可以看出储能系统在短期功率预测与实际出力相差较大时,出现了长时间出力受限,容量大面积缺额。

图11 2016年7月9日储能系统控制策略跟踪效果图

图12 2016年7月9日储能系统实际出力曲线与期望曲线

表3 数据样本2计算结果
由表3可知,使用储能系统的控制策略后,将日前短期功率准确率由71.11%,提高至74.74%。
如果在当天预测水平的基础上希望进一步提高风电场短期功率预测准确率,则需要增配储能,本文计算了将每一点预测准确率均提高至85%时的出力情况,如图13所示,至少需要60 MW的储能系统。
(3)数据样本3(2016年9月10日)
图14为9月10日风电场日前预测曲线、实测曲线和风储联合出力曲线,未使用储能前,准确率为95.36%,使用储能控制策略后,准确率为99.64%。

图13 增配储能后的出力效果

图14 2016年9月10日储能系统控制策略跟踪效果图
在短期功率预测准确率较高的时候,对储能系统出力要求低,图15为储能系统期望值与实际出力曲线,几乎重合,储能系统SOC也一直工作在较窄的范围内,如图16和表4所示。

图15 2016年9月10日储能系统实际出力与期望出力
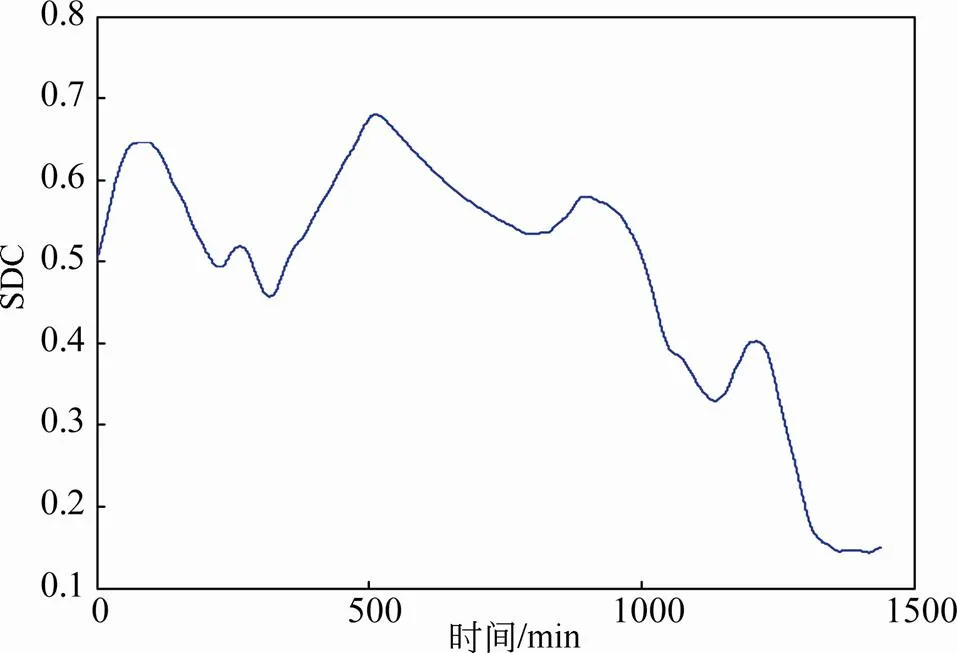
图16 2016年9月10日储能系统SOC变化曲线

表4 数据样本3计算结果
统计该风电场全年风功率短期准确度数据,并应用上述方法增配储能系统,可见从全年统计情况来看,按照100∶14的储能配比,提高风功率预测准确率4.49%。如果调度管理机构将风功率预测准确度的考核阈值划定为80%,则在当前样本数据下,100 MW风电场配置14 MW/63 MW·h储能系统可以满足风电场减少风功率预测准确度考核处罚的目标要求,见表5。
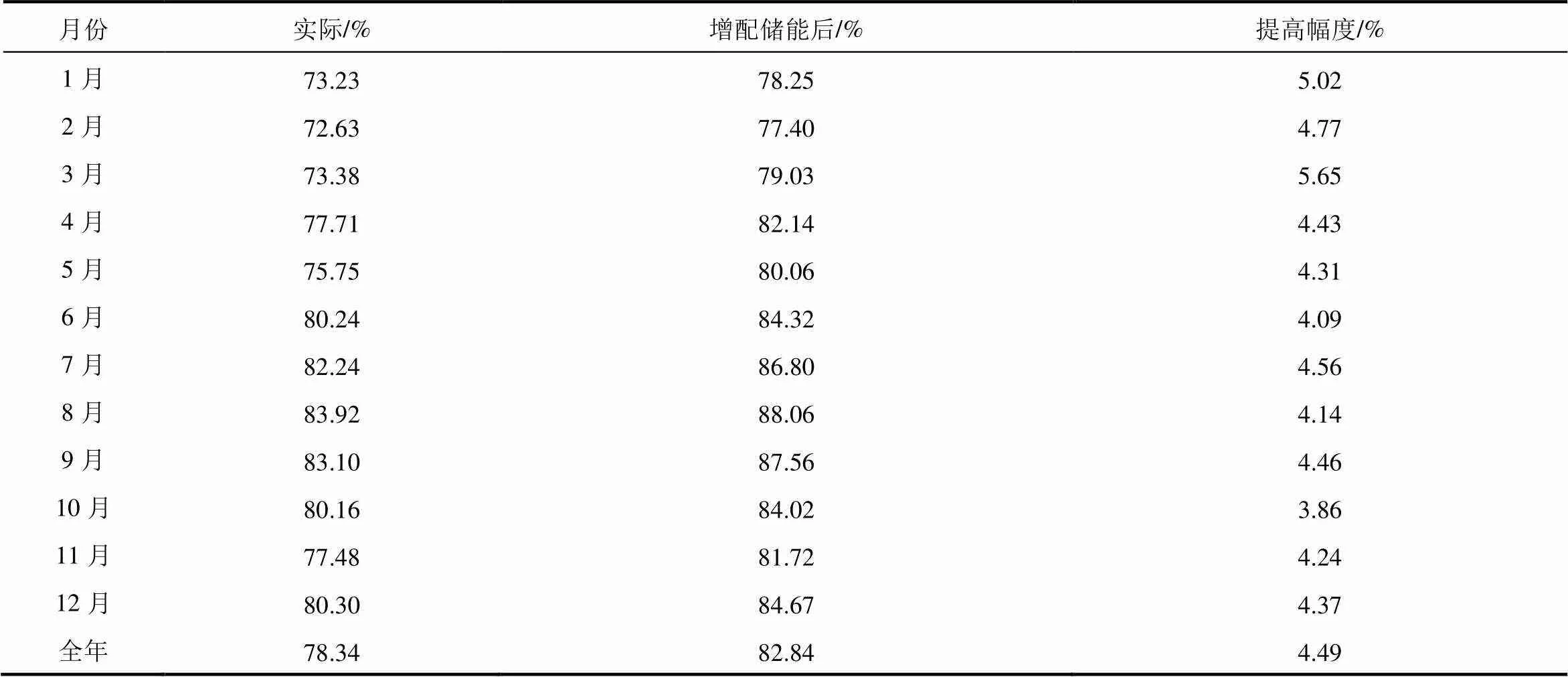
表5 全年风电场风功率预测准确度统计
4 结 论
本文以提高风电场短期功率预测准确率和合格率为目标,通过给风电场配置一定容量储能系统,研究储能系统出力控制策略。综合应用线性外推法和移动平滑法快速预测风电场实时出力,同时考虑储能系统安全工作范围和不同SOC区间内的出力能力,控制储能系统出力。选取较为典型的算例验证了本文提出的储能系统控制策略,可以提高风电场短期功率预测准确率,减少风电场考核损失,结论如下:
(1)基于线性外推和移动平均法的风电场实时出力预测方法,实测值和预测值最大偏差小于8%,满足储能系统能量管理控制的精度要求。
(2)选取多个较为典型的算例验证了本文提出的储能系统控制策略,可以提高风电场短期功率预测准确率,减少风电场短期功率预测准确率考核,同时能够保证储能系统始终工作在安全工作区域。
(3)风电场可以根据自身短期风功率预测水平,通过配置储能系统,达到减少短期功率预测准确度考核的目的。
[1] 刘冰, 张静, 李岱昕, 等. 储能在发电侧调峰调频服务中的应用现状和前景分析[J]. 储能科学与技术, 2016, 5(6): 909-914.
LIU Bing, ZHANG Jing, LI Daixian, et al. Energy storage for peak shaving and frequency regulation in the front of meter: Progress and prospect[J]. Energy Storage Science and Technology, 2016, 5(6): 909-914.
[2] 张静. 2015年储能市场盘点—一个蓄势待发的产业[J]. 储能科学与技术, 2016, 5(1): 58-64.
ZHANG Jing. Summary of 2015 energy storage market—A poised industry[J]. Energy Storage Science and Technology, 2016, 5(1): 58-64.
[3] 李琼慧, 王彩霞, 张静, 等. 适用于电网的先进大容量储能技术发展路线图[J]. 储能科学与技术, 2017, 6(1): 141-146.
LI Qionghui, WANG Caixia, ZHANG Jing, et al. A roadmap for large scale energy storage for grid-level applications[J]. Energy Storage Science and Technology, 2017, 6(1): 141-146.
[4] 陈跃燕, 李相俊, 韩晓娟, 等. 基于移动平均法和风电波动率约束的电池储能系统平滑风电出力控制策略[J]. 电力建设, 2013, 34(7): 1-5.
CHEN Yueyan, LI Xiangjun, HAN Xiaojuan, et al. Control strategy of smoothing wind power output using battery energy storage based on moving average method and wind power volatility rate costrain[J]. Electric Power Construction, 2013, 34(7): 1-5.
[5] LI X. Fuzzy adaptive kalman filter for wind power output smoothing with battery energy storage system[J]. IET Renewable Power Generation, 2012, 6(5): 340-347.
[6] 彭思敏. 电池储能系统及其在风-储孤网中的运行与控制[D]. 上海: 上海交通大学, 2013.
PENG Simin. Battery energy storage system and its operation and control in the isolated grid based on wind-battery[D]. Shanghai: Shang hai Jiao Tong University, 2013.
[7] 姚勇, 朱桂萍, 刘秀成. 电池储能系统在改善微电网电能质量中的应用[J]. 电工技术学报, 2012, 27(1): 85-89.
YAO Yong, ZHU Guiping, LIU Xiucheng. Improvement of power quality of micro-grids by battery energy storage system[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 85-89.
[8] 张野, 郭力, 贾宏杰, 等. 基于电池荷电状态和可变滤波时间常数的储能控制方法[J]. 电力系统自动化, 2012, 36(6): 34-38.
ZHANG Ye, GUO Li JIA Hongjie, et al. An energy storage control method based on state of charge and variable filter time constant[J]. Automation of Electric Power Systems, 2012, 36(6): 34-38.
[9] FARA L, BARTOK B, MORARU A G, et al. New results in forecasting of photovoltaic systems output based on solar radiation forecasting[J]. Journal of Renewable and Sustainable Energy, 2013, 5(4): 284-296
[10] CHEN K, SONG M X, ZHANG X. A statistical method to merge wind cases for wind power assessment of wind farm[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2013, 119(119): 69-77.
[11] SHARMA A, TYAGI V V, CHEN C R, et al. Review on thermal energy storage with phase change materials and applications[J]. Renewable & Sustainable Energy Reviews, 2009, 13(2): 318-345.
[12] ZHANG Q, LAI K K, NIU D, et al. A fuzzy group forecasting model based on least squares support vector machine (LS-SVM) for short-term wind power[J]. Energies, 2012, 5(9):3329-3346.
[13] 严干贵, 冯凯翔, 刘嘉, 等. 基于风电功率预测误差区间的储能系统控制策略[J]. 储能科学与技术, 2015, 4(4): 388-393.
YAN Gangui, FENG Kaixiang, LIU Jia, et al. A control strategy for energy storage system based on wind power prediction error interval[J]. Energy Storage Science and Technology, 2015, 4(4): 388-393.
The energy storage system output control strategy to improve the short term wind power forecasting accuracy rate
LI Na1,2,BAI Kai1,2,LIU Yu1,2,WANG Kairang1,2,GONG Yu1,2,DONG Jianming1,2
(1Wind-Solar-Energy Storage Hybrid Power Generation Technology Laboratory, Beijing 100045, China;2North China Electric Power Research Institution, State Grid Corporation of China, Beijing 100045, China)
At present, literature research on the energy storage system which is applied to control the fluctuation of new energy power generation and the control strategy of peak load shifting and valley filling has been done. Nevertheless, the feasibility of the application of the energy storage system under the mechanism of wind power prediction accuracy and the impact of wind farm benefits has not been studied. This paper proposes a control strategy of the system output to reduce wind farm short-term power prediction error for the target storage, which treats the real-time output data of wind farm (second level) as the data source and adopts the linear extrapolation method to predict the output of the wind farm at the next moment by moving average optimization. By comparing the short-term power forecast value and the real-time forecast value of wind farm and calculating the expected output of the energy storage system, simulation verification is carried out eventually after the output capacity of the energy storage system is restrained according to the output capacity of the SOC interval in the different energy storage system. The results show that the proposed control strategy of energy storage power system, can help the wind farm to meet the requirement of the short-trem power prediction accuracy assessment through the allocation of energy storage system, and has the guiding significance of lean-oriented operation and management of wind farm.
energy storage system; short term wind power forecasting; accuracy rate; state of charge(SOC)
TM 72
A
2095-4239(2018)01-100-08
10.12028/j.issn.2095-4239.2017.0130
2017-07-27;
2017-08-25。
国家电网公司科技项目(52018K16005V)。
李娜(1986—),女,硕士,高级工程师,大容量储能系统运行技术,E-mail:qiboer@163.com。
