铅酸电池开路电压的测量及其与累积放电量的关系

王 曦，伍联营，张伟涛，胡仰栋



铅酸电池开路电压的测量及其与累积放电量的关系

王 曦，伍联营，张伟涛，胡仰栋

（中国海洋大学化学化工学院，山东 青岛 266100）

铅酸电池开路电压与累积放电量的关系是铅酸电池模型的基础，对电池内电化学反应、传质过程等研究有重要意义。用恒流放电法测得了30次放电过程中电压和累积放电量的数据；提出了一种基于实验数据拟合外推获得开路电压的方法，由此获得的开路电压比传统方法更合理；基于电极反应速率和电解质浓度的平方成正比的假设，推导了开路电压-累积放电量的分段线性关系模型，并用遗传算法对模型参数进行了关联，结果与实验数据吻合良好。

荷电状态；铅酸电池；开路电压；累积放电量

开路电压（OCV，）和累积放电量（）的关系（-图）是电池模型的基础[1]，也是描述电池特性的重要数据[2]。

-图一般通过电池的恒流放电获得[3]。如以0.1C恒流放电[4]，在第次测量时，放电一定时间使累积放电量为Q，停止放电2 h，测得的电压作为开路电压U，持续放电到截止电压为止，将所有U、Q绘成-图。这样测得的开路电压实际上是近似的。

基于-图，许多学者发展了用于电池管理的数学模型，其中有经验的等效电路模型，如Rint 模型[5]、Thevenin模型[6-7]、一阶RC模型[8]、二阶RC[9]模型等。这类模型不考虑电池内部反应，将电池等效为一个包含电压源、电阻、电容和电感的电路，电池状态可以由电流、电阻等参数的变化辨识得到。同时，一些算法被用来为等效电路模型提供支持，如电化学阻抗谱法[10]、神经网络算法[11]和卡尔曼滤波法[12-13]等。

另外，一些学者在-图的基础上，考虑电池内离子的扩散、迁移和电极反应过程，发展了半经验的数学模型[14]。这些模型通过模拟充放电过程中电解质浓度和固液相电势的变化，来估算电池的状态[15]。近年，CFD技术被应用到这类模型的建模 中[16]，ESFAHANIAN等[17]和AMIR等[18]对模型进行了改进，提高了CFD计算速度。

目前-关系大都直接对实验数据进行经验拟合[16-18]，对OCV的测量也不尽合理。本文提出了一种基于实验数据拟合外推获得OCV的方法，可以得到更可靠的OCV值。在实验数据的基础上提出了-的三段线性关系模型，并对模型参数进行了关联。

1 U-Q关系的测量

1.1 实验仪器与测量条件

测试电池采用超威6-DZM-12型动力铅酸电池（电压12 V，标称容量12 A·h），测试仪为美尔诺M9710可编程直流电子负载，测试室温为20 ℃。

1.2 测量方案

用恒流放电法对电池进行测试，放电倍率0.1 C（电流1.2 A），截止电压为10.8 V。每放出额定容量的5%（约0.6 A·h），停止放电2 h使电池内离子恢复均匀，测量电压值。每隔10 s自动记录电压、累积放电量值。图1为某次恒流放电实验获得的-曲线。

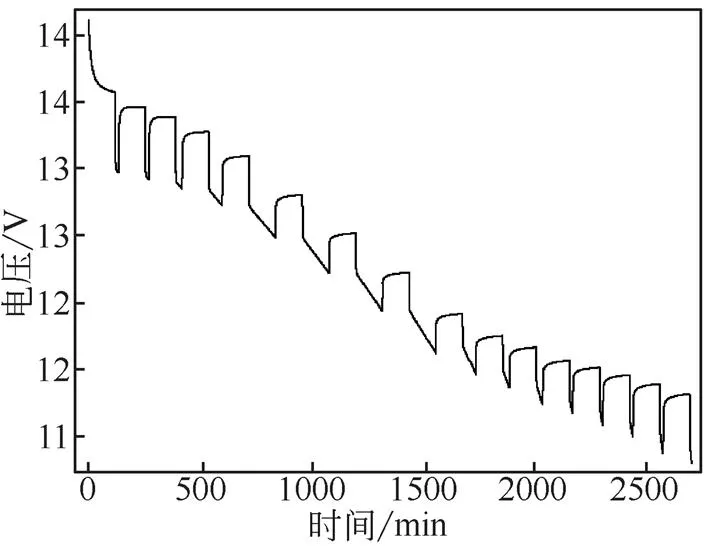
图1 某次放电测试的U-t曲线

1.3 U-Q图

1.3.1 充放电停止后电压随时间的变化

一般认为，充放电停止后2 h测得的电压为OCV，为弄清2 h是否足以使电池内离子恢复均匀，本文测定了充放电停止后电压随时间的变化。表1、表2分别是充电停止和放电停止后电压随时间的变化，结果显示，电压没有趋于稳定，说明2 h的静置时间不足以使电池内离子恢复均匀。

表1 充电停止后电压变化

表2 某次放电停止后电压变化

1.3.2 外推法确定OCV

在不大幅增加测试时间的前提下，为了获得更可靠的OCV，本文提出将充电/放电停止后电压变化的趋势模型化并令时间趋于无穷求得OCV的观点。对每次静置过程中电压变化数据进行拟合，并外推其极限，作为最终的OCV。

图2 充电停止后电压变化曲线拟合

图3 某次放电停止后电压变化曲线拟合

经多次尝试，本文最终确定，充电停止和放电停止后电压与时间的关系均可用式(1)表示。

这是个5参数模型，其中1、2为负值，当时间趋于无穷时，式(1)等号右边第二、三项均趋于0，此时，的极限0就是OCV。事实上，式(1)也可以写成式(2)的形式

前后两部分可以分别理解为正、负极对电压的贡献。

用式(1)对放电过程所有测量节点进行拟合外推，电压的变化如表3所示。

表3 外推前后电压的对比

2 U-Q关系模型的推导和参数的确定

2.1 三段线性模型

2.1.1 线性关系的推导

把实验测得的OCV与相应的累积放电量结合，得到铅酸电池-图（图4），可以看出，-关系整体上可以分为3部分，且都有较好的线性相关性，下文尝试推导-关系模型。

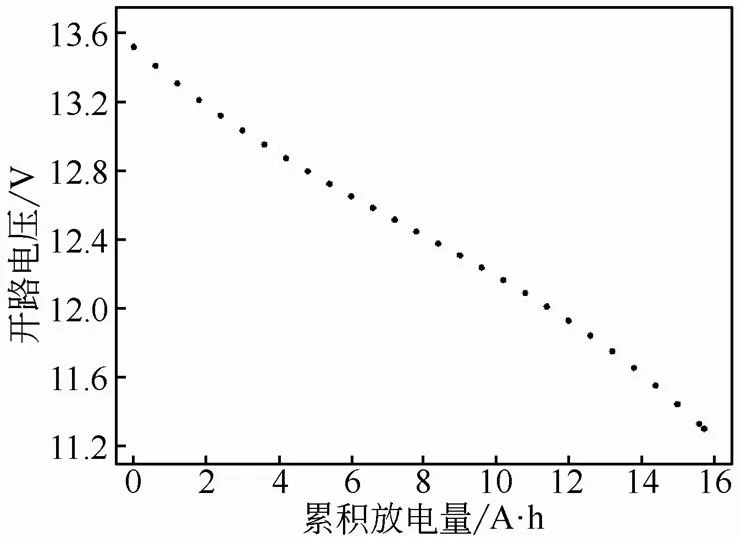
图4 铅酸电池U-Q关系

OCV是电池在开路状态下的路端电压（），此时电池内离子（对于铅酸电池主要指H+和HSO4-）均匀分布，最能反映电池的状态。虽然在电压测量过程中电路中仍有电流通过，但由于

通常认为，OCV等于电池的电动势[19]，即

铅酸电池的电极反应为

假设反应速度与电解质浓度的平方成正比

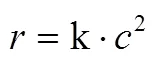
当溶液浓度较低时，电阻与电解质浓度成反比[20]

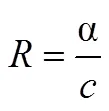
则OCV与电解质浓度有如下关系

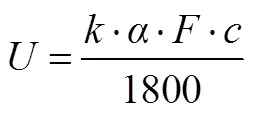
其中，与累积放电量有如下关系（为极板间可供反应的体积）

2.1.2 三段线性关系

铅酸电池稳定放电时的关系是线性的（图4），但放电初期和末期的情况有所不同。充放电过程中，电池正、负极上分别发生两个半反应：

假定极板上Pb、PbO2和PbSO4颗粒都为球形，由球体的性质可知，随着球体体积的均匀减少，球体表面积下降的速度会不断增大，并在体积趋于0时达到最大值。

放电初期，正极和负极均伴有PbSO4颗粒的成核过程，由于PbSO4的摩尔体积大于PbO2和Pb，正、负极孔隙率都会减小，同时PbSO4快速增大的表面积会显著影响PbO2/Pb和硫酸的接触，使OCV在累积放电量较小时显著下降。

放电末期，正极活性物质PbO2含量处于低位，此时PbO2颗粒可供反应的面积会快速下降，所以OCV也有显著下降。

在式(13)的基础上，考虑到放电初期和末期的不同，并进一步分别将它们简化为线性关系，得到-关系模型如下：

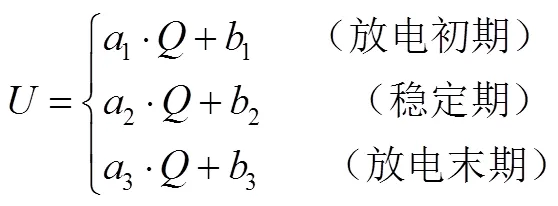
2.2 模型参数的确定

以图4的-关系为例，∈[0,15.7347]，用a、b两个决策变量把分为三个区间并进行拟合，使分段函数残差平方和最小的a、b组合为最优解。拟合曲线需要符合以下要求：

用遗传算法处理这个优化问题。分段函数残差平方和的倒数作为适应度，取种群数50，变异率0.01，杂交率0.7进行计算，每代种群中残差平方和的最小值变化趋势如图5所示。

最后得到的最优拟合结果见式(19)

图6 对U-Q关系的拟合结果

拟合系数由式(20)求得，结果为0.99947，可以看出拟合程度良好。

2.3 与文献模型的对比

式(21)为目前常用的经验模型[13,17-18]，经转化后与本文模型作对比，不难发现，电池型号的不同使二者电压在整体上有差别，但整体趋势上，本文提出的模型与文献一致。文献中的模型大致可以分为两段，与之相比，本文模型可以体现放电初始阶段OCV迅速下降的特征。

图7 文献中U-Q模型与本文模型的对比

3 结 论

（1）通过恒流放电实验测得了铅酸电池的-关系。

（2）提出了一种用外推原理测量OCV的方法，与传统方法相比，更为可靠。

（3）在电极反应速度与电解液浓度的平方成正比的假设下，在实验数据的基础上提出了OCV与累积放电量的分段线性模型，并对模型参数进行了回归，相关度大于0.999。

[1] 苏宪彬. LiFePO4锂离子电池放电行为理论研究[J]. 储能科学与技术, 2016, 5(4): 562-567.

SU X B. Theoretical study on discharge behavior of LiFePO4battery[J]. Energy Storage Science and Technology, 2016, 5(4): 562-567.

[2] 李文俊, 褚赓, 彭佳悦, 等. 锂离子电池基础科学问题(Ⅻ)——表征方法[J]. 储能科学与技术, 2014, 3(6): 642-667.

LI W J, CHU G, PENG J Y, et al. Fundamental scientific aspects of lithium batteries(XII)—Characterization techniques[J]. Energy Storage Science and Technology, 2014, 3(6): 642-667.

[3] CUGNTE M, LIAW B Y. Effect of discharge rate on charging a lead-acid battery simulated by mathematical model[J]. Journal of Power Sources, 2011, 196(7): 3414-3419.

[4] 徐杭田, 张国庆, 杨占录. 铅酸电池恒流放电特性灰色建模与仿真研究[J]. 信息技术, 2014, 7(2): 106-108.

XU H T, ZHANG G Q, YANG Z L. Rseearch on the grey modeling and simulation of discharge characteristics of lead-acid battery[J]. Information Technology, 2014, 7(2): 106-108.

[5] CHAN H L. A new battery model for use with battery energy storage systems and electric vehicles power systems[C]//Power Engineering Society Winter Meeting, 2000, IEEE, 1: 470-475.

[6] SALAMEH Z M, CASACCA M A LYNCH W A. A mathematical model for lead-acid batteries[J]. IEEE Transactions on Energy Conversion, 1992, 7(1): 93-98.

[7] 郭毅锋. 铅酸动力电池等效电路模型参数辨识方法研究[J]. 科学技术与工程, 2012, 12(17): 4165-4170.

GUO Y F. Parameter identification method of equivalent circuit model of lead acid battery[J]. Science Technology and Engineering, 2012, 12(17): 4165-4170.

[8] 王标. 基于电池模型的汽车铅酸电池SOC在线估计方法研究[D]. 合肥: 合肥工业大学, 2015.

WANG B. Research on on-line SOC estimation of vehicular lead acid battery based on battery model[D]. Hefei: HeFei University of Technology, 2015.

[9] 张彦琴, 郭凯, 刘汉雨. 铅酸电池模型及参数辨识研究[J]. 蓄电池, 2013, 50(3): 140-144.

ZHANG Y Q, GUO K, LIU H Y. Research on equivalent model and its parameters identification of lead-acid batteries[J]. Battery, 2013, 50(3): 140-144.

[10] D’ALKAINE C V, MENGARDA P, IMPINNISI P R. Discharge mechanisms and electrochemical impedance spectroscopy measurements of single negative and positive lead-acid battery plates[J]. Journal of Power Sources, 2009, 191(1): 28-35.

[11] 韩丽, 戴广剑, 李宁. 基于GA-Elman神经网络的电池劣化程度预测研究[J]. 电源技术, 2013, 37(2): 249-250+309.

HAN L, DAI G J, LI N. Prediction of SOH of battery based on GA-Elman neural networks[J]. Chinese of Power Technology, 2013, 37(2): 249-250+309.

[12] 胡振宇, 吴雷. 基于UKF的铅酸蓄电池SOC估算策略[J]. 江南大学学报(自然科学版), 2015, 14(5): 567-571.

HU Z Y, WU L. SOC Estimation of lead-acid batteries based on the Unscented-Kalman filtering[J]. Joural of Jiangnan University (Natural Science Edition), 2015, 14(5): 567-571.

[13] 钟国彬, 何耀, 刘新天, 等. 基于高阶非线性模型的铅酸蓄电池SOC估计[J]. 蓄电池, 2015, 52(4): 166-169.

ZHONG G B, HE Y, LIU X T, et al. SOC estimation of lead-acid battery based on high-order-nonlinear fitting model[J]. Battery, 2015, 52(4): 166-169.

[14] GU H, NGUYEN T V, WHITE R E. A mathematical model of a lead-acid cell: Discharge, rest, and charge[J]. Journal of the Electrochemical Society, 1987, 134(12): 2953-2960.

[15] GU W B, WANG C Y, LIAW B Y. Numerical modeling of coupled electrochemical and transport processes in lead-acid batteries[J]. Journal of the Electrochemical Society, 1997, 144(6): 2053-2061.

[16] ESFAHANIAN V, ANSARI A B, BAHRAMIAN H, et al. Design parameter study on the performance of lead-acid batteries[J]. Journal of Mechanical Science and Technology, 2014, 28(6): 2221-2229.

[17] ESFAHANIAN V, ANSARI A B, TORABI F. Simulation of lead-acid battery using model order reduction[J]. Journal of Power Sources, 2015, 279(1): 294-305.

[18] ANSARI A B, ESFAHANIAN V, TORABI F. Discharge, rest and charge simulation of lead-acid batteries using an efficient reduced order model based on proper orthogonal decomposition[J]. Applied Energy, 2016, 173(1): 152-167.

[19] 凌仕刚, 吴娇杨, 张舒, 等. 锂离子电池基础科学问题(ⅫⅠ)——电化学测量方法[J]. 储能科学与技术, 2015, 4(1): 83-103.

LING S G, WU J Y, ZHANG S, et al. Fundamental scientific aspects of lithium ion batteries(XIII)— Electrochemical measurement[J]. Energy Storage Science and Technology, 2015, 4(1): 83-103.

[20] 刘成伦, 徐龙君, 鲜学福. 水溶液中盐的浓度与其电导率的关系研究[J]. 中国环境监测, 1999, 15(4): 21-24.

LIU C L, XU L J, XIAN X F. Study on the relationship between concentration of salt sulution and conductivity[J]. Environmental Monitoring in China, 1999, 15(4): 21-24.

Measurement of open circuit voltage of lead-acid battery and its relation to cumulative discharge capacity

WANG Xi, WU Lianying, ZHANG Weitao, HU Yangdong

(College of Chemistry and Chemical Engineering, Ocean University of China, Qingdao 266100, Shandong, China)

The relationship between open circuit voltage and cumulative discharge capacity of lead-acid battery is the basis of lead-acid battery model, which has significant effect for the study of electrochemical reaction and mass transfer process in the battery. The data of voltage and accumulated discharge capacity during 30 times discharge processes were measured by constant current discharge method. A method to obtain open circuit voltage based on fitting and extrapolating with experimental data is proposed, which is more reasonable than the traditional one. A piecewise linear relation model for open circuit voltage and cumulative discharge capacity is derived which is based on the assumption that the rate of electrochemical reaction is in direct proportion to the square of the electrolyte concentration. Then the segmented nodes of the model are optimized by genetic algorithm before parameters are related, the results are in good agreement with the experimental data. It provides theoretical support for the study of reaction mechanism in lead-acid battery.

state of charge; lead-acid battery; open circuit voltage; cumulative discharge capacity

TM 912.1

A

2095-4239（2018）01-075-05

10.12028/j.issn.2095-4239.2017.0120

2017-07-03；

2017-07-10。

国家自然科学基金项目（21376231）。

王曦（1990—），男，硕士研究生，主要研究方向为蓄电池，E-mail：wangxi130205@163.com；

伍联营，教授，主要研究方向为过程系统工程，E-mail：wulianying@ouc.edu.cn。