六点三重插值-逼近混合细分法的研究①

朱 洪

(安徽三联学院基础部，安徽 合肥 230601)

0 引 言

细分法是由初始控制多边形的控制网格不断细化而产生的光滑曲线曲面的一类造型方法。其算法简单高效，容易实现等优势，因此在计算机辅助几何设计等领域中有着广泛的应用。Dyn等[1]和Deslauriers等[2]分别提出C1连续的四点二重插值细分和四点三重插值细分。为了提高细分算法的光滑性，Hassan等[3]C2四点三重插值细分方法。Siddiqi等[4]利用Lagrange多项式基函数提出了2N点三重细分算法，当N=2,3,4时，极限曲线的连续阶数分别为C3,C4,C5。Siddiqi等[5]和胡玫瑰等[6]给出了C2连续的六点插值细分法和C4连续的六点细分算法。汪钵等[7]提出了一类含参数的细分法，对于三参数的五点二重逼近算法可达C6连续。Tan等[8]提出C2连续的四点二重细分，同时对保形性进行了探讨。庄兴龙等[9]提出C7连续的五点二重逼近细分算法。张艳艳等[10]提出了含有双张力参数的C2连续五点插值细分法。檀结庆等[11]提出从三重插值细分中推导逼近细分的方法，同时产生的曲线为C2连续。王栋等[12]将插值逼近两种细分格式相结合，从而生成C2连续的极限曲线。虽然逼近细分法能够使得产生的曲线更加光滑，但是不能很好的控制初始多边形，而插值细分法对于初始控制多边形较为依赖，能够有效保持原来的形状。基于上述研究，将六点三重细分算法的掩模引入张力参数，统一插值逼近两种细分格式，并对参数进行适当取值，从而得到一系列的插值曲线和逼近曲线。

1 预备知识

(1)

定理1[3]若三重细分算法S一致收敛，则掩模α={ai}满足

(2)

定理2[3]设三重细分算法S的掩模α={ai}满足式(2)，则存在一个三重细分算法S1，满足

dPk=S1dPk-1

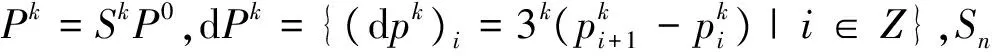
(3)

2 六点三重插值-逼近混合细分法及连续性分析

(4)

其中，a0=a4=-α，a1=a3=4α，a2=1-6α,

定理4 对于任意给定的控制多边形，当α=0,-0.0062<β<0.0556时，式(4)生成的插值曲线是C1连续的，当β=0,-0.0031<α<0.0741时，式(4)生成的逼近曲线也是C1连续的。

证明：

因为a=(ai)={…,b5,b0,a0,b4,b1,a1,b3,b2,a2,b2,b3,a3,b1,b4,a4,b0,b5,…}

∴a(z)=b5z-8+b0z-7+a0z-6+b4z-5+b1z-4+a1z-3+b3z-2+b2z-1+a2+b2z+b3z2+a3z3+b1z4+b4z5+a4z6+b0z7+b5z8

由定理2知，S1的生成多项式为

i=-6,-5,…,8

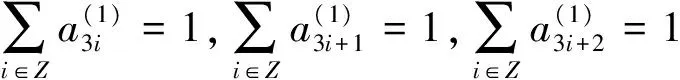
当-0.0031<α<0.0741,-0.0062<β<0.0556时，

因此，由定理3可知，该细分法是一致收敛的。

再根据定理2，

i=-4,-3,…,8

当-0.0031<α<0.0741,-0.0062<β<0.0556时，

根据定理3，式(4)C1连续。

定理5 对于任意给定的控制多边形，当0.0041<α<0.0185,β=0时，式(4)生成的逼近曲线是C2连续的。

证明： 根据定理2，

i=-2,-1,…,8

当0.0041<α<0.0185,β=0时，

根据定理3，式(4)C2连续。

定理6 对于任意给定的控制多边形，当0.0168<α<0.0173,β=0时，式(4)生成的逼近曲线是C3连续的。

证明： 根据定理2，

i=0,1,…,8

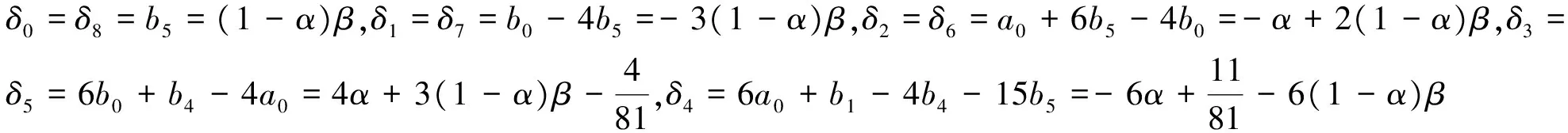
当0.0168<α<0.0173,β=0时，

根据定理3，式(4)C3连续。

3 算 例

通过统一插值细分和逼近细分两种细分格式，给出插值-逼近六点三重混合细分法。在同一个初始控制多边形下，当α=0,β=-0.006,-0.001,0,0.01,0.02,0.03,0.05时，得到一系列极限曲线插值于控制顶点，如图1(a)、(b)所示；当β=0,α=-0.003,-0.02,0,0.005,0.01,0.017,0.03时，生成一系列逼近的极限曲线，如图1(c)、(d)所示。

图1

结合插值细分法和逼近细分法的各自优势，对插值-逼近混合细分算法中的两个张力参数进行适当取值，使得产生的极限曲线能够灵活调控。当α=0.017且β=0,0.01,-0.01,0.02-0.02时，生成一系列六点插值-逼近混合细分曲线，如图2所示；当β=0且α=0,0.01,-0.01,0.02-0.02时，生成一系列细分曲线，如图3所示。

4 结 语

通过引入张力参数将插值算法与逼近算法进行统一，且张力参数可以反映出插值算法及逼近算法两者之间的紧密联系。未来工作将对该细分算法的保形性以及动态的其它细分格式作具体研究。

[1] Dyn N, Levin D, Gregory J A. A 4-point Interpolatory Subdivision Scheme for Curve Design[J]. Computer Aided Geometric Design, 1987, 4(4): 257-268.

[2] Deslauriers G, Dubuc S. Symmetric Iterative Interpolation Processes[M].Constructive Approximation. Springer US, 1989:49-68.

[3] Hassan M F, Ivrissimitzis I P, Dodgson N A, Sabin M A. An Interpolating 4-points Ternary Stationary Subdivision Scheme[J]. Computer Aided Geometric Design, 2002,19:1-18.

[4] Siddiqi S S, Rehan K. Ternary 2N-point Lagrange Subdivision Schemes[J]. Applied Mathematics and Computation, 2014, 249:444-452.

[5] Siddiqi S S, Noreen T. Convexity Preservation of Six Point Interpolating Subdivision Scheme[J]. Applied Mathematics and Computation,2015,265:936-944.

[6] 胡玫瑰,郑红婵,段建伟.四参数六点细分法[J].计算机工程与应用,2011,47(6):184-187.

[7] 汪钵,檀结庆.一类由Laurent多项式诱导的带参数二重细分[J].计算机辅助设计与图形学报,2016,28(12):2082-2087.

[8] Tan J Q, Zhuang X L, Zhang L. A New Four-point Shape-preserving Subdivision Scheme[J]. Computer Aided Geometric Design, 2014, 31: 57-62.

[9] 庄兴龙,檀结庆.五点二重逼近细分法[J].图学学报, 2012, 33(5): 57-61.

[10] 张艳艳,檀结庆.双参数五点插值细分法[J].计算机工程与应用, 2014, 50(6): 135-138.

[11] 檀结庆,童广悦,张莉.基于插值细分的逼近细分法[J].计算机辅助设计与图形学学报, 2015, 27(7):1162-1166.

[12] 王栋,张曦,李桂清.混合细分曲线及其应用[J].计算机辅助设计与图形学学报, 2007, 19(3): 286-291.

[13] 郑红婵,叶正麟,赵红星.双参数四点细分法及其性质[J].计算机辅助设计与图形学学报, 2004,16(8):1140-1145.