基于小波变换的电池阻抗测量及分析①

张珺涵

(上海同济大学汽车学院,上海 201804)

0 引 言

电化学阻抗谱(英文全称，Electrochemical Impedance Spectroscopy)是一种重要的电化学测试技术，已广泛应用于锂离子电池及材料的研究。研究表明，电池的阻抗与电池的SOH(英文全称，State-of-Health)和SOC(英文全称，State-of-Charge)之间有着较明显的对应的关系[1～2]，不仅如此，无法通过测量而得到的电池内部温度也可以通过电池当前的阻抗角计算得到[3]，这些都是表征电池性能的重要参数。因此，获取电池的阻抗信息十分重要。

首先通过理论推导和对比实验验证利用小波计算电池阻抗的可行性，然后通过改变温度和电池荷电状态，研究了利用小波计算的方法和EIS测量设备所获得的阻抗的异同，并对差异来源进行了分析，最后对实验结果进行总结。

1 基于小波变换的电池阻抗计算模型

目前，获取电池阻抗信息主要是通过直接测量和算法辨识两种途径[4]。辨识主要是基于最小二乘、卡尔曼等方法的电池等效电路模型参数估计[5～6]，进而得到电池阻抗信息，其不足之处在于等效电路模型并不能真实反应电池的阻抗信息。为了获得真实的阻抗信息，阻抗的直接测量逐渐成为研究的热点。小波变换作为时间频率局部化分析的一种方法，在平移伸缩参数的条件下实现对信号在高频处时间细分，低频处频率细分，从而克服傅里叶变换的不足，在处理非平稳信号中有出色的表现。

图1 实验台架示意图

小波变换通过平移母小波获得信号的时间信息，而通过缩放小波的宽度获得信号的频率特性。对于一个连续信号f(t)，其连续小波变化定义如下：

(1)

在小波分析中，小波函数的形式是多种多样的，选择复Morlet函数作为小波基函数，复Morlet函数的定义如下：

(2)

从式(2)中可以看出，复Morlet函数由高斯函数和正弦函数两部分组成，其中fc表示函数的中心频率，fb表示带宽变量。fc的选择应根据原始信号和分析目标来决定[7]。fc决定了小波函数的中心频率。具体的fb值选择，可以参考天津大学王教授等人的研究[8]。

日本东京大学的Yoshinao Hoshi等人[9]，采用阶跃电压或电流信号对电池进行激励，通过对输入信号和响应信号进行小波变换，进而得到电池的阻抗信息。利用小波变换计算阻抗的原理如下

(3)

(4)

(5)

2 实验方案介绍

2.1 实验台架

实验采用方形的8Ah磷酸铁锂电池型号为IFP1780123P，航天电源技术有限公司生产，充放电设备为Chroma BA500，采样设备为NI USB-6210，电化学工作站为Solartron 1287/1255B，采样电阻Rs=10mΩ。图1为实验台架搭建的示意图。

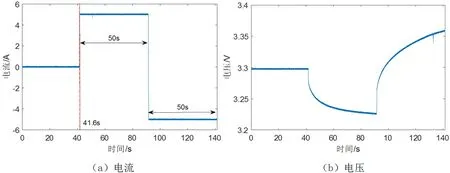
图2 电池两端的电压和电流信号

图3 小波变换与EIS设备得到的阻抗对比图

2.2 实验步骤

实验过程为将处于70%SOC、50%SOC、30%SOC的电池，在45℃、35℃、25℃、15℃、5℃、-5℃的温度下进行放电实验(放电电流为5A，采样频率10kHz)和EIS测量实验，研究电池在不同SOC和不同温度的条件下，小波变换计算得到的阻抗结果与电化学工作站测量得到的EIS的异同。

具体的实验步骤如下：

第一步：电池置于恒温箱内，对电池进行室温(25℃)下的电池容量标定实验，并充满至100%SOC，然后在室温(25℃)下1C放电至70%SOC。

第二步：将恒温箱温度调至45℃，静置1.5小时。

第三步：利用电化学工作站对电池进行EIS测量实验。

第四步：再静置1.5小时，对电池进行50秒的放电实验，放电电流为5A，然后再进行50秒的充电实验，充电电流也为5A。充放电期间用NI USB-6210采集卡采集电池上的电压和电流信号，采样频率为10kHz。

第五步：将恒温箱调节至35℃，25℃，15℃，5℃，-5℃，各静置1.5小时。并分别重复第三、四步实验。

第六步：将恒温箱调节至室温(25℃)，静置1.5小时，然后1C放电至50%SOC，重复上述第二、三、四、五步实验。

第七步：将恒温箱调节至室温(25℃)，静置1.5小时，然后1C放电至30%SOC，重复上述第二、三、四、五步实验。

3 实验结果及讨论

以处于70%SOC的电池在25℃下为例，其放电电压和电流如图2所示。

选择fc=10kHz，fb=6×10-9s2，尺度参数a的选取参考EIS设备测量的频率，电压和电流信号在开关瞬间发生变化，因此选择时间参数b=41.6s，然后根据式(3)算出电池阻抗，选取其中0.0278Hz到316.2Hz作为研究区间，并与相同条件下的EIS结果进行对比，如图3所示。

从图3中可以看出，在中频部分，利用小波变换求得的阻抗与EIS测得的阻抗基本保持一致，在高频和低频部分，利用小波变换求得的阻抗与EIS测得的阻抗有所偏差。分析产生这种偏差的原因，在低频部分，由于利用小波变换的方法为了保证信噪比，采用了较大的激励信号，从而导致了电池内部的非线性，而根据Fathima Fasmin等人的研究[10]，当激励信号过大时，响应信号的低频部分会产生很大的谐波，这些低频的谐波会叠加在相同频率的响应信号中，导致结算结果有偏差。而在高频部分，一方面是是受到激励信号和响应信号的高频噪声影响，另一方面根据海森堡的不确定性原理，在信号的时频分析中，信号的时间分辨率增加，频率分辨率就会降低，反之亦然，因此无法保证信号在时间和频率上都有良好的分辨率，会产生计算误差。除此之外，阻抗角在高频时非常小，加之以上原因，导致了小波计算的结果与EIS测量结果产生了偏差。

3.1 温度的影响

在同一SOC点(70%SOC)，电池处于不同温度时的测量结果如图所示。

图4 不同温度下，小波变换与EIS设备得到的阻抗对比图

图4为不同温度下利用小波变换求得的阻抗与EIS测量的阻抗的对比图，从图4可以看出在高频段，利用小波变换求得的阻抗与EIS测量的阻抗差异不大。当温度为-5℃时，发现两种方法获得的阻抗在中频段和低频段有很大差异。当温度为5℃时，两种方法获得的阻抗在中频段和低频段的差异都有所减小。随着温度升高，中频段几乎没有差异，低频段差异仍然存在。这是因为当电池温度处于低温时，电池内部的离子运动很弱，EIS测量阻抗的方法是准稳态方法，小激励信号对电池内部离子扩散运动影响较小，而利用小波变换的方法采用较大的激励，会使电池内部离子运动加剧，从而使得扩散环节在阻抗谱中的作用占据很大部分，阻抗发生变化。随着温度升高，电池内部离子扩散系数变大，激励对于电池内部离子运动的影响越来越小，因此中频段阻抗的差异随着温度的升高越来越小，直至几乎没有差异。低频段的阻抗差异虽然随着温度的升高也会减小，但是差异会一直存在，这部分差异就是上文提到由于激励下的谐波引起的。

3.2 SOC的影响

在同一温度下，电池处于不同SOC时的阻抗如图所示。

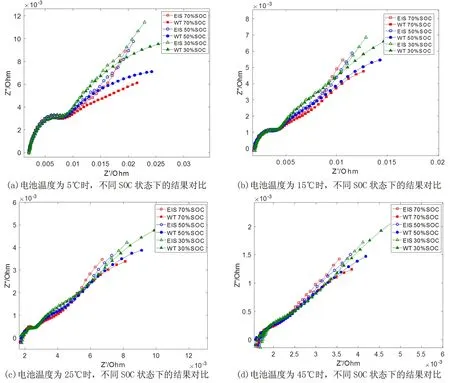
图5 同一温度，不同SOC条件下的阻抗对比图

从图5中可以看出，随着电池温度的升高，处于不同SOC状态下的电池其EIS测量的阻抗与小波计算的阻抗偏差减小，这与之前的结果保持一致。在同一温度下，可以观察到电池的SOC越小，利用小波变换得到的阻抗与EIS测量的阻抗在低频时的阻抗谱偏离角度越小，但是同频率下阻抗点发生了较大偏移。这是由于在电池处于低SOC状态时，电池内部的锂离子更容易在电流作用下形成较大的浓度差，使得低频部分阻抗变大，在图中也可以看出，低频部分小波计算得到的阻抗要大于EIS测量的阻抗。

4 结 论

相比以往获取电池阻抗的方法，运用小波变换理论得到的阻抗在运算速度上有着非常突出的表现，虽然在低频部分由于为了增加信噪比而使用了较大的电流使得电池内部出现非线性响应，导致低频内阻偏差较大，但是如果能够减小硬件设备噪声，减小激励电流，从而减小低频内阻偏差，会使测量结果更加准确。

通过改变温度和电池荷电状态，研究了两种方法所测量阻抗的异同，在同一SOC下，利用小波计算得到的阻抗与EIS测量的阻抗差异受到温度影响，随着温度升高，差异逐渐变小，中高频阻抗基本吻合，低频阻抗略有偏差。在同一温度下，可以观察到电池的SOC越小，利用小波变换得到的阻抗与EIS测量的阻抗在低频时的阻抗谱偏离角度越小，但是同频率下阻抗点发生了较大偏移。

[1] Macdonald, D.D., Reflections on the history of electrochemical impedance spectroscopy. Electrochimica Acta,2006 .51(8-9):p.1376-1388.

[2] 李革臣,古艳磊.电化学阻抗谱法预测锂电池荷电状态[J].电源技术,2008,32(9):599-602.

[3] Zhu, J.G., et al., A new lithium-ion battery internal temperature on-line estimate method based on electrochemical impedance spectroscopy measurement. Journal of Power Sources, 2015.274: p.990-1004.

[4] Troltzsch, U., O. Kanoun, and H.R. Trankler, Characterizing aging effects of lithium ion batteries by impedance spectroscopy. Electrochimica Acta, 2006.51(8-9): p.1664-1672.

[5] 戴海峰,魏学哲,孙泽昌.基于等效电路的内阻自适应锂离子电池模型[J].同济大学学报：自然科学版, 2010, 38(1): 98-102.

[6] 马辰杰,赵小巍,杨林. 基于等效电路电池模型参数辨识方法的适应性研究[J]. 机电一体化,2015,21(04).

[7] 蒋永华,汤宝平,董绍江. 自适应Morlet小波降噪方法及在轴承故障特征提取中的应用[J]. 仪器仪表学报,2010,31(12):2712-2717.

[8] Wang, G.F., Wang, T.Y., Ren C.Z., Li, H.W., Wang, X.B. (2004),“Application of Complex Shifted Morlet Wavelet in Vibration Monitoring of Spindle Bearing of Crank Shaft Grinder” Key Engineering Materials,vols. 259-260,pp.697-701.

[9] Hoshi, Y., et al. Wavelet transformation to determine impedance spectra of lithium-ion rechargeable battery. Journal of Power Sources, 2016.315: 351-358.

[10] Fathima Fasmin, Ramanathan Srinivasan. Review—Nonlinear Electrochemical Impedance Spectroscopy. Journal of The Electrochemical Society,164 (7) H443-H455 (2017).