基于多元统计的PM2.5分析与预测—以合肥地区为例①
2018-02-05敖希琴费久龙陈家丽汪金婷
敖希琴, 费久龙, 陈家丽, 郑 阳, 汪金婷
(安徽新华学院信息工程学院,安徽 合肥 230088))
0 引 言
近年来中国环境污染日益严重,许多城市出现雾霾天气,监控和预测大气污染已成为空气质量研究中的一个重要部分。PM2.5指的是大气中粒径小于或等于2.5μm的颗粒物,表示每立方米空气中这种颗粒的含量,其值越高,就代表空气污染越严重[1]。PM2.5从客观上对空气中的细小微粒能够做出描述和衡量,体现空气中微粒的浓度,已经成为人们日常生活中一个不可或缺的一项空气质量指标。
由于对PM2.5造成影响的因素有很多,统计分析中的多元回归分析模型可以处理这种情况,并且在气象、经济等领域已经有相当多的研究。例如唐猛分析了PM10浓度的统计学分布及预测[2];赵广华等将多元回归模型应用在区域经济预测中[3]。由国内诸多的文献可以看出,多元回归分析是预测方法中一种比较主流的的方法,在以往的研究中得到广泛的应用。
1 多元线性回归
多元线性回归分析是以多个解释变量的给定值为条件的回归分析,是研究一个因变量和多个自变量之间的线性关系方法[4],多元线性回归模型的一般形式为:
Y=β0+β1X1+β2X2+β3X3+…+βjXj+…
+βkXk+μ
(1)
式中,K为解释变量的数目,βj(j=1,2,…,k)为回归系数,μ为去除k个自变量时对Y影响后的随机误差。
2 模型数据准备
2.1 数据收集
为验证多元统计方法在PM2.5分析及预测方面的适用性,选取了合肥地区的PM2.5数据进行了相关实验。数据来源于“天气后报网[5]”,选取了时间段为2015年1月至2015年12月全年数据进行分析。
2.2 数据预处理
2.2.1 数据的筛选
由于该网站提供的数据项目比较多,基于实验目的,将2015年全年的数据中的“AOI指数”、“当天AQI排名”这两列数据剔除,剩下的“日期”、“质量等级”、“PM2.5”、“PM10”、“SO2”、“NO2”、“CO”、“O3”等列保留。
2.2.2 数据处理
该网站提供的数据当中,经过排查,出现了若干缺失值,需要进行填补,以满足数据的完整性要求。实验缺失值的处理方法是利用简单(非随机)插补,即用某个值(如平均值、中位数、众数)来替换变量中的缺失值,此处采用缺失值相邻两个值的平均值进行替代。
数据中存在一些影响模型效果的观测点,这些观测点或大或小,需要对其进行排查处理,以减小异常值对于整个数据模型的影响。异常值是指样本中的个别值,其数值明显偏离它所属样本的其余观察值[6]。对于异常值,可以通过箱线图判断。
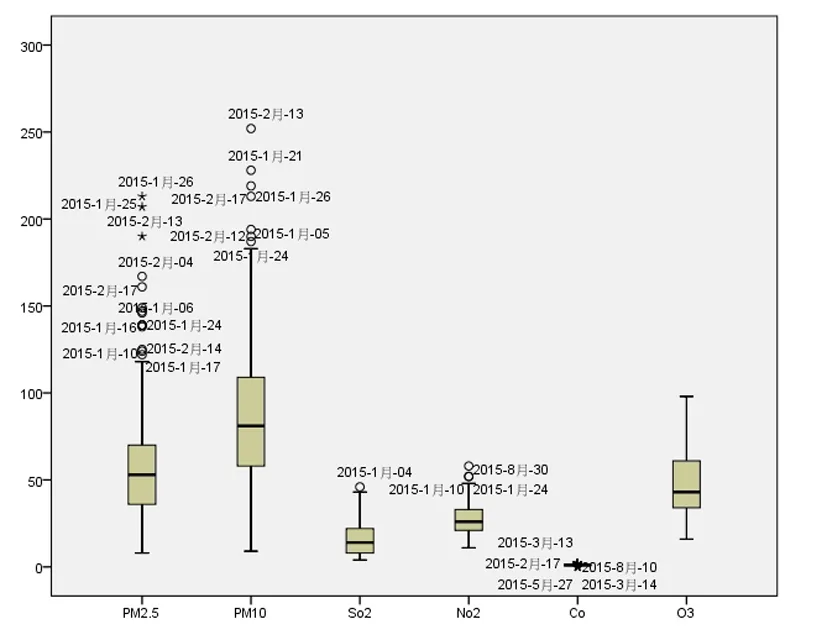
图1 箱线图
由图1可以看出,数据中存在着一些异常值,如2015年1月17日、2015年1月25日、2015年2月04日、2015年2月14日、2015年2月17日、2015年5月27日、2015年8月10日等异常值。采取的处理方法是直接删除异常值。
2.2.3 数据分割
为体现实验的科学性,将合肥地区2015年的数据进行分割,2015年1月1日至2015年9月30日的数据为实验数据集,用于分析建模;2015年10月1日至2015年12月31日的数据为验证数据集,用于验证模型预测的准确性。
3 模型建立
3.1 相关性分析
相关分析是指对不同变量进行定量分析,由此来判断他们之间是否存在较为密切的关系,以及关系的密切程度。课题研究的是PM2.5和各个影响因素的关系,因此首先要进行PM2.5和各个影响因素相关性的考察,可以通过观察变量间的散点图来进行相关性分析。
借助于R软件,可做PM2.5和各个影响因素之间的散点图,如图2所示。并计算二者之间的相关系数,如表1所示。

表1 PM2.5与各影响因素间相关系数
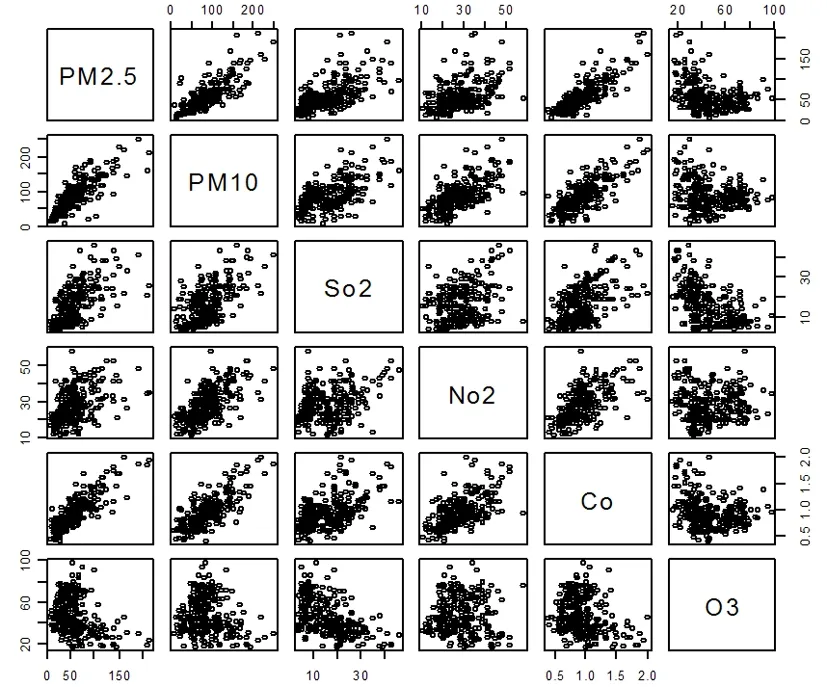
图2 综合散点图
由图2可观察到PM2.5和PM10、CO之间有较为明显的线性趋势关系,其关系系数分别为0.803和0.838;PM2.5和SO2、NO2之间有一定的线性趋势关系,其关系系数分别为0.615和0.456,这四个影响因素与PM2.5呈正相关,说明当其浓度高增大时,PM2.5的浓度也会相应的增大。而PM2.5和PM10之间的散点图较为分散,其关系系数为-0.343。
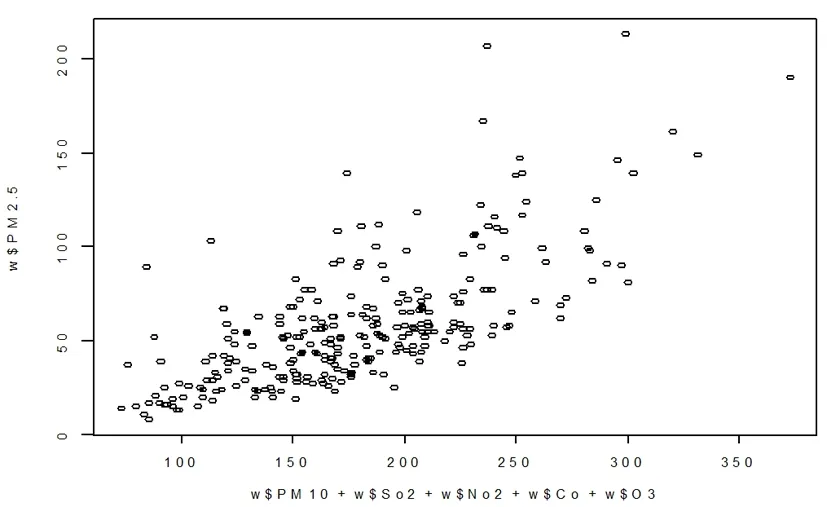
图3 五个影响因素为整体时与PM2.5之间的散点图
3.2 多元回归模型的建立
通过相关性分析的结果,可以发现PM2.5与各个变量之间的关系基本呈现出线性趋势,为更好地研究PM2.5与各个影响因素之间的关系,选择PM10、SO2、NO2、CO、O3五个影响因素为自变量,建立多元回归模型。
首先将五个影响因素看成整体,做与PM2.5之间的散点图,从而大致的判断点的趋势,如图3所示。
从图3中可以看出大概呈现出线性的趋势,于是借助于R软件建立多元线性回归方程,得到结果如表2所示。
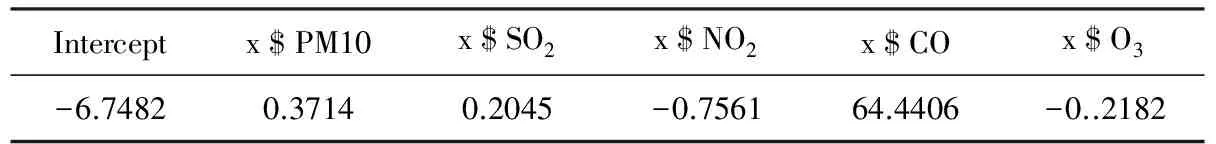
表2 系数表
根据实验结果,可得到该多元线性回归模型的表达式:
PM2.5=0.37PM10+0.20SO2-0.76MO2+
64.44CO-0.22O3-6.75
(2)
3.3 模型的检验
为验证模型的有效性,采用拟合优度检验、方程显著性检验、参数显著性检验对模型进行检验和评价。
3.3.1 拟合优度检验
在多元线性回归模型中,Multiple R-Square为决定系数,又称拟合优度,反映了自变量对因变量解释程度的高低,其值越大,说明自变量对因变量解释程度越高;Adjusted R-Square为可调整的拟合优度,反映了回归方程对样本的拟合程度,其值越大,回归方程对样本的拟合程度越高。借助于R软件中的summary函数,可得到拟合优度检验结果,如表3所示:

表3 拟合优度检验结果
由表3可知,Multiple R-Square的值为0.813,Adjusted R-Square的值为0.810,接近于1,表明拟合优度较好。
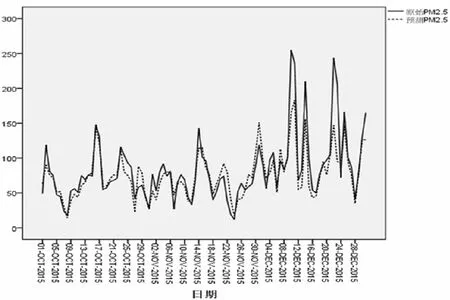
图4 预测值与实际值的对比图
3.3.2 方程显著性检验
在多元线性回归模型中,方程的显著性检验通常用F检验,即当p-value<0.05,即通过显著性检验。通过R软件,计算出来的p-value小于2.2e-16,远小于0.05,即满足显著性要求。
3.3.3 参数显著性检验
在多元线性回归模型中,参数的显著性检验是对自变量的显著性进行判定,即当Pr(>|t|)<0.05,通过显著性检验。借助于R软件中的summary函数,可得到参数显著性检验结果,如表4所示。

表4 参数显著性检验结果
由表4可知,除SO2剩余四个自变量均通过参数显著性检验。但是结合实际来看,SO2显然是对PM2.5有影响的。而作为模型选择的重要方法之一,逐步回归分析法可以用来筛选模型。
3.4 模型筛选
3.4.1 逐步回归分析
逐步回归就是在许多自变量共同影响着一个因变量的关系中,判断哪个( 或哪些) 自变量的影响是显著的,哪些自变量的影响是不显著的,然后将影响显著的自变量选入和将影响不显著的变量剔除[7],逐步回归分析结果如表5所示。

表5 逐步回归分析模型参数分析
由表5可知,又得到了一个预测模型:
PM2.5=0.37PM10+0.20SO2-0.76MO2+
64.44CO-0.22O3-6.75
(3)
由逐步回归分析可知,相对于原来的模型,新模型去除SO2、为验证新的模型是否满足课题需要,同理采用拟合优度检验、方程显著性检验、参数显著性检验等指标验证模型。
其中拟合优度检验结果,Multiple R-Square的值为0.8117,Adjusted R-Square的值为0.8089,相比于原来的模型,略有下降;方程显著性检验中,p-value: < 2.2e-16,可以得知方程通过了显著性检验;方程的显著性检验结果中,所有自变量均通过参数显著性检验。
3.4.2 模型选择
AIC准则又称最小信息准则,是衡量统计模型拟合优良性的一种标准,是寻找可以最好地解释数据但包含最少自由参数的模型,因此优先考虑的模型是应该是AIC最小的一个[8]。
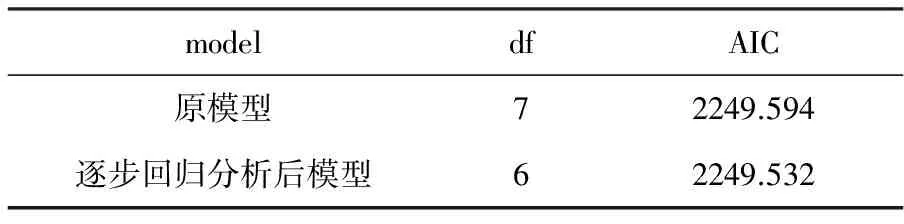
表6 AIC模型比较
从上述实验结果,可以发现第二种模型的AIC相对较小,并且在考虑自变量尽可能少的原则下,选择逐步回归分析后的模型为最终的预测模型。
PM2.5=0.30PM10-0.76NO2+64.16CO-
0.26O3-3.51
(4)
3.5 模型的预测
通过以上分析得到的模型,用于预测合肥市2015年10月至12月合肥市的PM2.5。采用均方根误差(RMSE)准则(公式5)、平均绝对误差(MAE)准则(公式6)和Theil不相等系数准(公式7)则用于检验模型的预测效果,并做预测值与实际值的对比图如图4所示。
(5)
(6)
(7)
其中yi表示真实值,gi表示预测值,RMSE值和MAE值都是越小,表示预测值与真实值越接近,预测准确度越高;U取值在0到1之间,U越接近0,模型预测越准确。
由公式可得均方根误差(RMSE)为24.56,平均绝对误差(MAE)为15.65, Theil不相等系数为0.14,由于PM2.5的数据是在0~500甚至更大范围内波动,相比之下,该预测模型的RMSE、MAE、和Theil不相等系数较为理想,由此推断模型整体预测效果较好。
4 结 语
通过分析合肥市2015年PM2.5相关数据,建立一种以PM2.5为核心的多元线性回归模型。该模型指标共包括PM10、SO2、NO2、CO、O3五项。通过建立PM2.5与各个指标之间的散点图,大致判断各个指标是否与PM2.5呈现出一定的线性关系,从而建立一个“强行”的多元线性回归模型;采用拟合优度检验、方程显著性检验、参数显著性检验以及逐步回归分析对模型进行验证;最后得到一个较为满意的模型。运用该模型预测了2015年合肥市10月至12月份的PM2.5,且拟合优度和调整的拟合优度分别为0.81,0.81,均方根误差(RMSE)为24.56,平均绝对误差(MAE)为15.65,Theil不相等系数为0.14,模型预测效果较好。
虽然提出的多元线性回归模型可以在一定程度上较好的预测PM2.5,但仍然存在一些不足,具体如下:
1)该模型在建模前剔除了异常值,所以得到的模型较为稳健,对于一些较为极端的天气,预测效果不理想,如何将这些异常值纳入预测模型,提高模型对极端天气的预测准确性,这方面的工作有待进一步研究。
2)结合实际分析来看,PM2.5的变化与时间存在一定的关系,可以在多元线性回归模型的基础上结合时间序列模型,从而得到一个更为精确的模型。
[1] 百度百科.PM2.5.https://www.sogou.com/sie?hdq=AQxRG-4492&query=PM2.5&ie=utf8.
[2] 唐猛.长沙市颗粒物PM10浓度统计学分布特性与预测[D].长沙:中南大学,2010.
[3] 赵广华,刘炜.多元回归模型在经济预测区域中的应用[J].中国商贸,2009(08):180-181.
[4] 张景阳,潘光友.多元线性回归与BP神经网络预测模型对比与运用研究[J].昆明理工大学学报(自然科学版),2013,38(06):61-67.
[5] 天气后报网.http://www.tianqihoubao.com/ .
[6] 王怀亮.统计数据异常值的识别及r语言实现[J].电子技术,2012(05):6-8.
[7] 姜新华,刘霞,薛河儒,等.基于逐步回归的空气质量影响因素分析——以呼和浩特市区为例[J].内蒙古农业大学学报(自然科学版),2015,36(02):123-126.
[8] Guofeng, SongXiaogang, DongJiafeng etc. Blockwise AIC for Model Selection in Generalized Linear Models[J].Environmental Modeling & Assessment, 2017 (1) :1-11.
