基于灰色模型的风速概率分布参数预测

李牡丹，王印松，李亚玲

(华北电力大学 a.科技学院；b.控制与计算机工程学院，河北 保定 071003)

0 引言

我国风能资源丰富，近年来风能在能源结构中所占比例逐渐增大。取之不尽用之不竭的风资源给我国的电力事业带来飞跃式的发展，装机容量已赶超美国，成功跃居世界首位。然而随着进一步的发展，越来越复杂的地形和多变的气候对风场选址提出了更高的要求，预示着对风资源的研究迫在眉睫。对于风电来说，不仅需要政府的大力投资，而且需要更加精准地评估复杂地形的风资源，这是风电场成功建设的重要前提[1]。

风速概率分布参数是描述风资源统计特性的一个重要指标，也是风场规划设计和并网技术研究中的一个必要参数[2-4]。威布尔(Weibull)分布和瑞利(Rayleigh)分布是拟合风速概率分布较常用的模型，其中以两参数Weibull 分布模型应用最为广泛。模型参数常采用最小误差逼近算法、最小二乘法、均值和方差估算等算法进行计算。

文献[5]采用平均风速参与因子对区域风资源进行评估。假设风速服从两参数Weibull分布，通过合理选取不同地理位置多个观测站的数据，采用矩量法计算风速分布参数。当观测站数据庞大时该方法有良好的评估效果，精度较高，但当数据有缺失时，就很难准确地分析出风资源的规律，因此对数据的要求较高。文献[6]选取美国国家环境预报中心(NCEP)气象数据和航天飞机雷达地形测绘任务(SRTM)地形数据作为数据源，对高海拔山区进行风资源评估，并采用反距离插值法获得风速分布参数。该方法适合用来评估一些数据不容易得到或地形复杂气候多变的区域，对测量卫星的精度有较高要求。文献[7]建立了混合神经网络模型，利用不同的训练方法对混合神经网络进行训练，并采用自适应粒子群算法优化神经网络参数，将观测站的历史数据代入模型中获得风电场的历史风速特征，进而对风速分布参数进行计算与对比，仿真结果表明该方法具有较高的精度。文献[8]基于计算流体力学(CFD)建立了能够逼真模拟复杂地形三维风场大气流动的k-ε湍流模型，并利用实测风速数据建立了一种风资源评估方法。针对短期或平稳变化的风速序列，以上这些方法预测效果较好，但需要数量较多且精度较高的实际风速数据，若历史风速序列数据少且波动性大，采用上述方法对风速分布参数进行预测将变得极为困难[3]。

本文提出采用灰色Verhulst模型对风速分布参数进行预测，假设风速服从两参数Weibull分布。首先将历史风速数据按月拟合，把平均风速和标准差代入Weibull分布公式计算每年的分布参数，并对得到的数据进行检验与分析；然后代入灰色Verhulst模型进行对比与分析，并根据所获得的历史参数规律预测未来年份相应的分布参数值。计算结果表明，灰色Verhulst模型可以利用很少的历史数据得到较高精度的结果，可以根据风速分布参数的规律模拟得到未来年份相应的风速分布参数，为风电场资源评估提供理论依据。

1 风速概率分布模型及参数拟合

1.1 风速概率分布模型

假设从气象站获得的风速序列服从Weibull分布，则其分布函数为

(1)

概率密度函数为

(2)

式中：v为随机变量风速，m/s；V为从气象站获得的风速序列，V=(V1，V2，…，Vn)；k和c分别为Weibull分布形状参数和尺度参数，m/s，后者表征风电场的平均风速。

1.2 基于灰色理论的参数预测模型

灰色系统理论[9-10]由邓聚龙教授于1982年提出，该方法可以在样本数据较少且服从规律未知的情况下，通过微分拟合，将无规律的原始数据序列变换成有一定规律的时间数据序列，从而对不确定的非线性系统数据序列进行预测。尤其是灰色Verhulst模型能有效削弱原始数据序列中不规则数据的随机性，适合对具有波动特性的数据序列进行预测。

灰色Verhulst参数预测模型的输入为风场最近几年相同月份的分布参数数据序列

X(0)={X(0)(1)，X(0)(2)，…，X(0)(n)} ，

(3)

式中：n为数据序列的维数。

对原始参数数据序列进行累加后，得到一次累加序列(1-AGO)为

X(1)={X(1)(1)，X(1)(2)，…，X(1)(n)} 。

(4)

为了避免外界因素对原始数据序列的影响，本文借鉴灰色预测GM(1，1)模型对原始数据序列的检验方法[11]，对一次累加序列分别进行数据光滑性规律检验和指数性规律检验，以确保原始数据的光滑性和精度。

光滑性规律检验：

(5)

当k>3时，ρ(k)<0.5(k=4，5，…，n)成立。

指数性规律检验：

(6)

当k>3时，σ(k)∈(1，1.5)(k=4，5，…，n)成立。 利用1-AGO构造灰色Verhulst预测模型的一阶白化非线性方程

(7)

式中：a，b为灰色模型系数，利用式(8)进行估计。

(a，b)T=(BTB)-1BTY

(8)

(9)

Y=[x(2)x(3) …x(n)]T。

(10)

由此得原始序列的预测值为

(k=1,2,…,n) 。

(11)

灰色模型适合于变化比较平缓的序列，否则可能会导致检验无法通过。为此，可以把上述灰色Verhulst模型参数预测结果当成原始序列再一次代入灰色模型进行计算，同样可以取得较高的预测精度[3]。

1.3 预测结果检验

本文通过定义原始序列方差、参差序列方差和残差，采用后验差法对灰色Verhulst参数预测模型的预测结果进行检验，方法如下[9]。

(12)

(13)

(14)

(15)

(16)

式中：C为残差标准差与原始序列标准差的比值，C越小表明预测值越接近实际值，预测精度越高；P为小误差概率，表示残差偏差落在某个区间内的概率，P越大越好。综合C和P两个指标就可以评价灰色Verhulst参数预测模型的精度，精度等级评价标准见表1。

2 算例分析

本文采用某风电场气象站采集的2006—2015年的历史风速相关数据，首先利用均值和方差估算法计算出这10年间12个月基于双参数Weibull分布的原始风速分布参数值k和c，见表2。

表1 精度等级评价标准

表2 风速分布参数 m/s

2.1 参数预测

将2006—2015年间同一月的10个风速分布参数值作为原始数据序列，代入灰色Verhulst模型计算出下一年对应的参数预测值。本文以参数k为例说明预测步骤。

(1)对10个原始k值进行累加，得到1-AGO。

12.07，13.84，15.63，17.28} 。

(17)

(2)对1-AGO分别进行光滑性和准指数规律性检验，检验结果见表3。

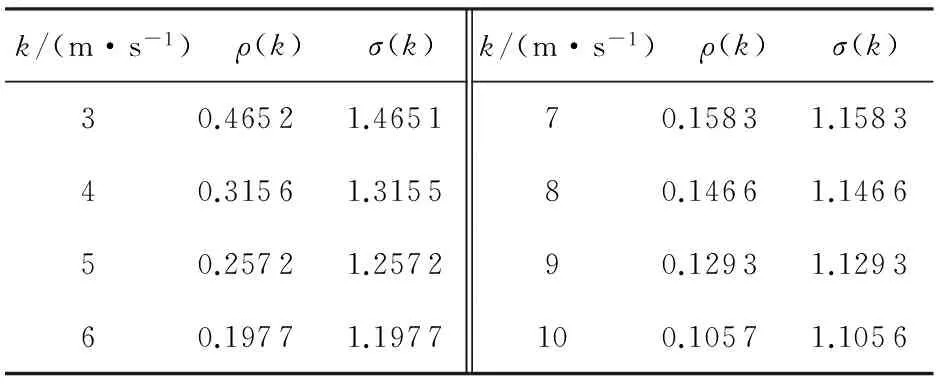
表3 原始参数检验结果

由表3可以看出，当k>3 m/s时，满足ρ(k)<0.5(k=4，5，…，n)，σ(k)∈(1,1.5)，故检验都能通过。

(3)构建一阶白化非线性方程，经计算得到未知参数a=0.004 7，b=1.042 6，因此参数拟合方程为

(k=1,2,…,n) 。

(18)

(4)对表4的结果进行检验，计算得到C>0.65，P<0.70，结合表1可知，预测结果精度不符合要求。

表4 灰色Verhulst模型预测数据

2.2 参数二次预测

本文为了得到更高精度的k值预测结果，把上述灰色Verhulst模型预测值作为原始序列进行第2次预测。

(1)对参数k再一次累加，得到

8.785 4，10.516 5，12.239 0，13.953 0，

15.658 5，17.355 6} 。

(19)

(2)进行光滑性和准指数规律性检验，检验结果见表5。

表5 原始参数二次检验结果

可见，当k>3 m/s时，满足ρ(k)<0.5(k=4,5,…,n),σ(k)∈(1,1.5)，故分布参数k的检验都能通过。

(3)构建一阶白化非线性方程，得到参数拟合方程，将计算出的二次分布参数k的预测值与一次预测值比较，结果见表6。

表6 灰色Verhulst模型二次预测数据

(4)对表6中的预测结果进行检验，计算得出

C=S2/S1=0.002 923<0.35 ，

(20)

1>0.95 。

(21)

对照表1可知，k值预测精度为一级。为了进一步说明灰色Verhulst模型的预测效果，本文利用如下公式分别求出了2006—2015年k值二次预测值与原始值之间的绝对平均误差和相对均方根误差。

(22)

(23)

3 结束语

假设风速服从两参数 Weibull分布，采用灰色Verhulst模型对风速分布参数进行预测。首先将历史风速数据的平均风速和标准差代入Weibull分布公式计算出每年的风速分布参数，并对得到的数据进行检验与分析；然后代入到灰色Verhulst模型中进行对比与分析；最后根据获得的历史参数规律来预测得到未来年份相应的分布参数值。计算结果表明，灰色Verhulst模型可以利用较少的历史数据预测得到较高精度的风速分布参数，为风电场资源评估提供理论依据。

[1]宋婧.我国风力资源分布及风电规划研究[D].保定：华北电力大学，2013.

[2]申洪，王伟胜.一种评价风电场运行情况的新方法[J].中国电机工程学报，2003，23(9):90-93.

[3]丁明，吴伟，吴红斌，等.风速概率分布参数预测研究及应用[J].电网技术，2008，32(14):10-14.

[4]刘波，贺志佳，金昊.风力发电现状及发展趋势[J].东北电力大学学报，2016，36(2):7-13.

[5]吉平，周孝信，武守远.采用平均风速参与因子法的区域风资源评估[J].中国电机工程学报，2012，32(19):10-15.

[6]李云婷，葛莹，张杰，等.NCEP气象数据结合SRTM地形数据的高海拔山区风资源评估方法[J].电力建设，2014，35(11):112-116.

[7]王娜，周有庆，邵霞.基于混合神经网络的风电场风资源评估[J].电工技术学报，2015，30(14):370-376.

[8]梁思超，张晓东，康顺，等.基于数值模拟的复杂地形风场风资源评估方法[J].空气动力学学报，2012，30(3):415-420.

[9]邓聚龙.灰色系统基本方法[M].2版.武汉：华中科技大学出版社，2005.

[10]刘思峰，党耀国，方志耕，等.灰色系统理论及其应用[M].3版.北京：科学出版社，2004.

[11]丁明，吴义纯，张立军.风电场风速概率分布参数计算方法的研究[J].中国电机工程学报，2005，25(10):107-110.