基于“标准-3”动能拦截弹的顺轨拦截方法研究

，， ，

(1.解放军装备学院 研究生管理大队，北京 101416；2.解放军装备学院 航天装备系，北京 101416；3.解放军装备学院 航天指挥系，北京 101416)

0 引言

大气层外机动变轨是一种比较成熟的弹道导弹突防手段[1]，当拦截器对弹道导弹采用迎面撞击的方式进行防御时，两者之间的相对速度非常大, 末制导时间极短[2]，通常只有不到10 s的时间，不利于拦截器修正偏差和精确命中目标。在这样的情况下，采用顺轨拦截方式不失为一种明智的做法，顺轨拦截方式能够有效降低拦截器与目标之间的相对速度，延长拦截器的末制导时间，提高拦截器修正偏差的能力。2005 年7 月，美国NASA采用顺轨拦截方式成功实施了深度撞击计划[3]，印证了这一方法的有效性和可行性。

文献[4]对比分析了顺轨和逆轨拦截方式，证明了顺轨方式在修正能力和需用过载等方面具有优势，但制导过程采用了较为保守的平行接近法；文献[5]把拦截过程简化成两个正交的平面，设计了平面拦截的前向制导律，但没有扩展至三维空间，文献[6]设计了一种用于对弹道导弹实施中段顺轨拦截的二阶滑膜制导律，通过仿真验证了制导律的正确定，但在制导律引入了目前阶段拦截器导引头无法测量的目标加速度信息。此外，以上研究的仿真过程均建立在初始对准条件较好的情况下，没有考虑工程上拦截器所能达到的真实速度，导引头的测量误差以及动力学系统的响应延迟和饱和过载等因素。

本文严格依照美国“标准-3”拦截弹的公开参数，采用所需目标信息较少的自适应滑膜制导律，对大气层机动目标的顺轨拦截过程进行了仿真分析，验证了动能拦截器顺轨拦截方法的可实践性，对大气层外机动目标的防御具有积极意义。

1 顺轨拦截的定义

记拦截器在地心惯性坐标系下的速度矢量为Vm，目标在地心惯性坐标系下的速度矢量为Vt，则交会角Ψ可以表示为：

当90°≤Ψ≤180°时，交会方式称为顺轨拦截。

根据拦截器与目标的速度大小，顺轨拦截又可以定义为追击顺轨拦截和前置顺轨拦截，其中，追击顺轨拦截泛指拦截器速度大于目标速度的情况，前置顺轨拦截泛指拦截器速度小于目标速度的情况，图1为二者的交会示意图。

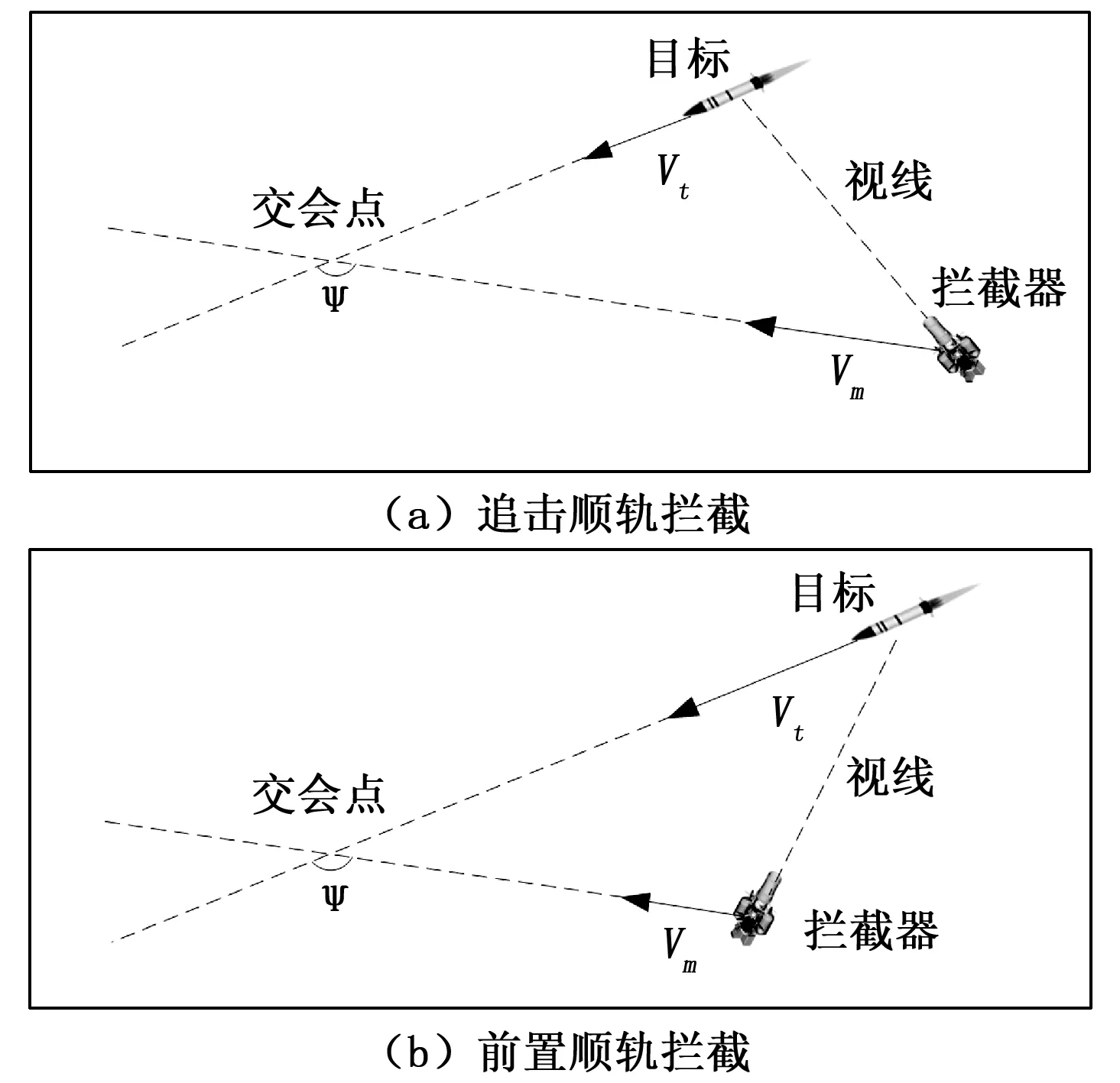
图1 顺轨拦截示意图

拦截器进行追击顺轨拦截时，从目标的后半球区域进行碰撞，进行前置顺轨拦截时，从目标的前半球区域进行碰撞，一般而言，大气层外拦截器的助推时间较短，速度在3～4 km/s之间，无法达到洲际弹道导弹的水平，因而，对前置顺轨拦截的研究更加具有现实意义。

2 顺轨拦截的数学模型

2.1 质心运动模型

本文采用球坐标描述双方的位置矢量和速度矢量，其中，位置矢量通过地心距r，地理经度λ(东经为正)和地理纬度φ(北纬为正)来表示，速度矢量通过速度大小v，当地速度倾角θ(速度矢量与地球表面的夹角，地球表面向上为正)和当地速度偏角σ(速度矢量在地球表面上的投影与正北方向的夹角，顺时针为正)来描述，6个参数的空间关系如图2所示。

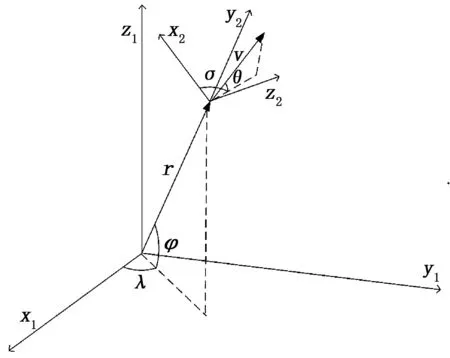
图2 模型参数空间示意图

为简化计算，忽略次要因素，可以认为地球是均匀的无旋球体，得到导弹质心的运动模型为：

式中：r为地心距、λ为地理经度，φ为地理纬度，v为速度大小、θ为当地速度倾角，σ为当地速度偏角；g为平均重力加速度，Fcxh、Fcyh和Fczh为控制力在航迹坐标系3个坐标轴方向上的投影大小。

2.2 相对运动模型

由六参数模型可以唯一确定拦截弹在地心惯性坐系下的位置矢量Rm(t)与速度矢量Vm(t)：

式中,

为地心惯性坐标系到北天东坐标系的转换矩阵。

同理，易知目标在地心惯性系下的位置矢量Rt(t)和速度矢量Vt(t)。

式中，e1(t)、e2(t)和e3(t)为视线坐标系3个坐标轴方向的单位向量，即：

2.3 制导控制模型

侧向指令采用自适应滑模制导律[7](ASMG)，拦截器侧向指令过载应为：

式中：aMy(t)、aMz(t)分别表示拦截器纵向和横向上的指令过载，N为导航比，k、η和δ为用来保证鲁棒性的参数。

拦截器所受到的轨控力矢量可以表示为：

Fc(t)=(aMy(t)·e2(t)+aMz(t)·e3(t))·mK(t)

为了将控制力矢量与质心运动模型对应起来，对其做如下转化：

Fcxh(t)=Fc(t)·ε1(t)

Fcyh(t)=Fc(t)·ε2(t)

Fczh(t)=Fc(t)·ε3(t)

式中，ε1(t)、ε2(t)和ε3(t)为航迹坐标系3个坐标轴方向的单位矢量，即：

那么，Fcxh(t)、Fcyh(t)和Fczh(t)即控制力矢量在航迹坐标系3个坐标轴上的投影。

2.4 质量模型

对于处于中段飞行的机动弹头，其质量mt(t)可以表示为：

其中：Pt(t)为机动力矢量，m0t为机动弹头的初始质量，It为机动弹头的燃料比冲，t0为初始时刻。当机动弹头不做机动时，其质量可以看作是不变的。

对于拦截弹，其质量mm(t)可以表示为：

mm(t)=∑mzi(t)+mk(t)

mzi(t)表示第i级助推火箭的质量：

其中：Pzi(t)为的推力矢量，m0zi为第i级助推火箭的初始质量，Izi为第i级助推火箭的燃料比冲，ti为第i级发动机开始工作的时刻。

mk(t)表示拦截器的质量：

其中：Fc(t)为拦截器的控制力矢量，m0k为拦截器的初始质量；Ik为拦截器的燃料比冲；tk为拦截器开始工作的时刻。

3 计算机辅助仿真分析

3.1 拦截场景设定

设预警系统探测到173°E，46°N处有一洲际导弹目标，初始地表高度为1 000 km，速度为6 000 m/s，弹道倾角为30°，弹道偏角为-90°，拦截弹阵地位于128°E，40°N处，采用顺轨拦截方式对目标进行防御。

拦截弹的助推火箭参数参照“标准-3”的MK72发动机、MK104发动机和MK136发动机设定[8]，如表1所示。

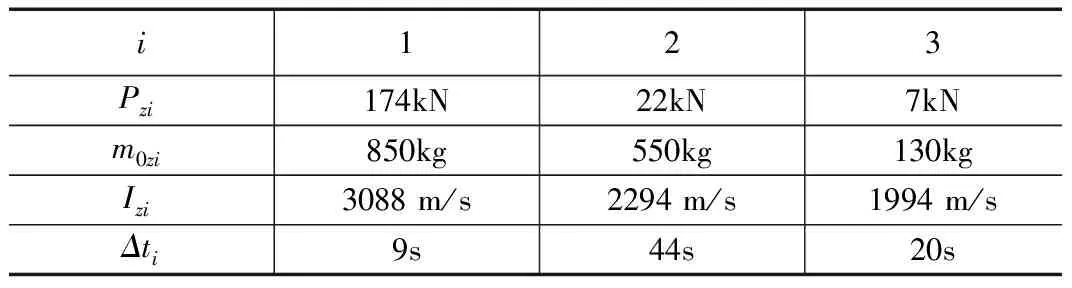
表1 助推火箭参数表

表中，Δti=ti+1-ti表示第i级助推火箭的总工作时长。

拦截器参数参照“标准-3”的“LEAP”大气层外轻射弹设定[9]，如表2所示。

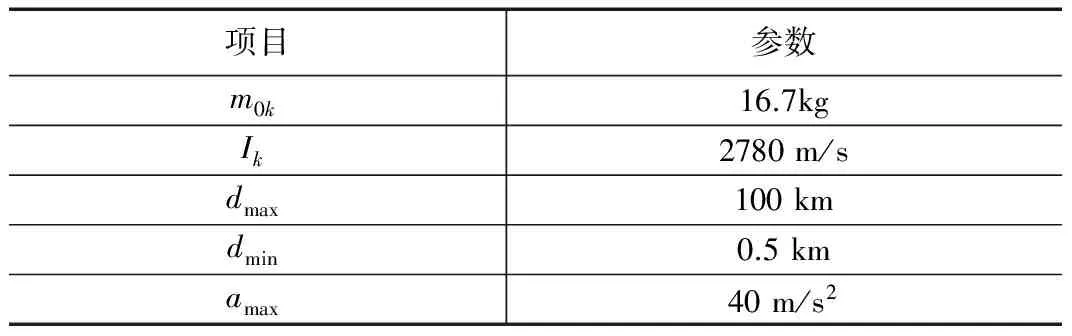
表2 拦截器参数表

表中，dmax和dmin分别表示拦截器导引头的最大探测距离和盲区，amax代表拦截器的饱和过载。

3.2 顺轨拦截窗口计算

弹道导弹已摧毁既定目标为最终目的，在没有遇到拦截的情况下不会主动进行机动，可以通过轨道外推的方法来求解发射诸元，对于顺轨拦截弹道，只要使拦截器与目标的交会角Ψ满足条件即可。

在拦截弹阵地位置已知的情况下，可以按照以下流程来计算拦截窗口：

STEP1：取足够小的初始当地倾角Δθ，初始当地偏角Δφ和时间间隔Δt，建立基于已知部署位置的拦截弹空间可达集Λ；

STEP2：用同样的时间间隔Δt，外推目标弹道τ；

STEP3：记初始时刻tp= 0 s，取空间点τ(tp)，判定拦截弹可达集中是否存在一点Λ(θ0,φ0,tf)同时满足以下3个条件：

1)到τ(tp)的距离dp<1 000 m；

2)拦截弹飞行时间tf≤tp；

3)交会角90°≤Ψ≤180°。

STEP4：若可达集中存在满足条件的点，计算拦截弹发射时间tl=tp-tf并储存，令tp=tp+Δt，回到STEP3，若不存在，直接令tp=tp+Δt，回到STEP3；

STEP5：检索至目标落地时刻结束。

计算当前场景的顺轨拦截窗口，如表3所示。

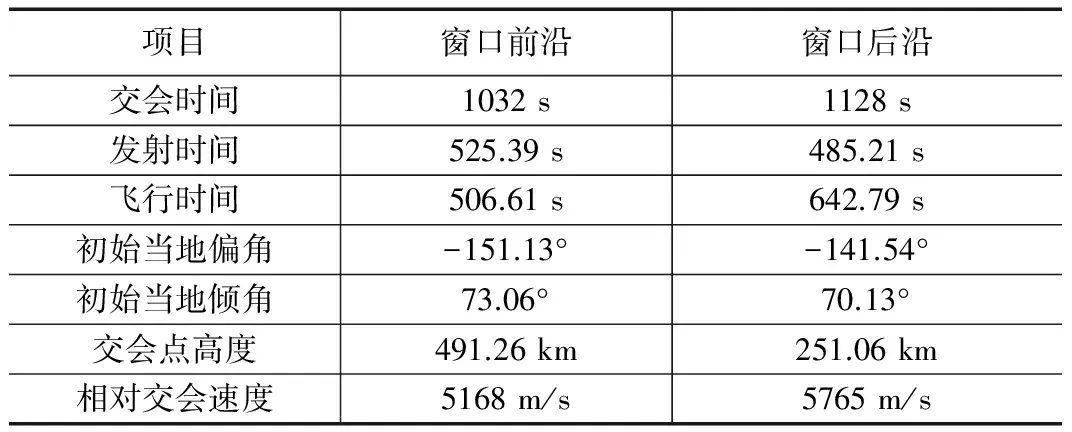
表3 拦截弹道数据表

由表3可以看出，在当前场景中，顺轨拦截窗口长度为96 s，目标弹道可拦截弧段的高度在260 km到452 km之间，相对交会速度约为5.5 km/s。另外，由于采用顺轨拦截方式时，拦截弹的飞行时间随着拦截时间的推移而增加，发射时间反而会提前，换而言之，拦截窗口的前沿对应着发射窗口的后沿，拦截窗口的后沿对应着发射窗口的前沿。

3.3 寻的制导过程仿真分析

选取拦截窗口中的一条顺轨拦截弹道，研究末制导阶段的拦截器过载情况，所选拦截弹道tl=506.89 s，θ0=73.78°，φ0=-149.17°，双方的空间飞行轨迹如图3所示：

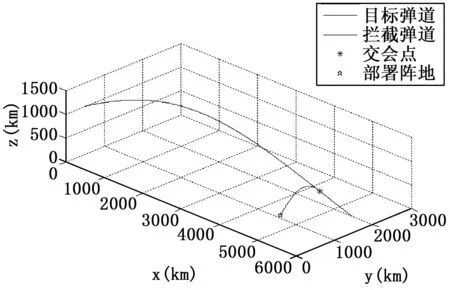
图3 顺轨拦截空间示意图

3.3.1 初始对准误差

由于实际控制误差的存在，双方不可能严格按照理论弹道飞行，当目标进入拦截器的导引头捕获距离时，双方的空间位置和飞行速度有可能严重偏离理论位置，故取目标和拦截器距离达到dmax时的位置矢量端点和速度矢量端点作为球心，分别在半径为1 000 m和100 m/s的空间球体内随机取点生成带有误差的位置矢量和速度矢量，作为末制导的仿真初值。

3.3.2 视线测量误差

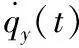
3.3.3 动力学约束条件

“标准-3”的拦截器“LEAP”弹头采用喷流直接力控制，响应速度远远高于气动力系统，控制精度可以达到0.01 s，仿真中采用两个采样周期作为动力学系统的延迟时间，为0.02 s[11-12]，此外，当目标与拦截器只见的距离达到dmin时，导引头无法继续提供视线转率信息，将拦截器的指令加速度置零。

3.3.4 末制导过载分析

令目标的纵向机动力Ptyh=10 000sin(πt/2)N，横向机动力Ptzh=10 000cos(πt/2)N，取制导参数N=3、k=2.1、η=0.5、δ=0.0 002 deg/s，得到视线转率和拦截器过载的仿真图线，如图4和图5所示。

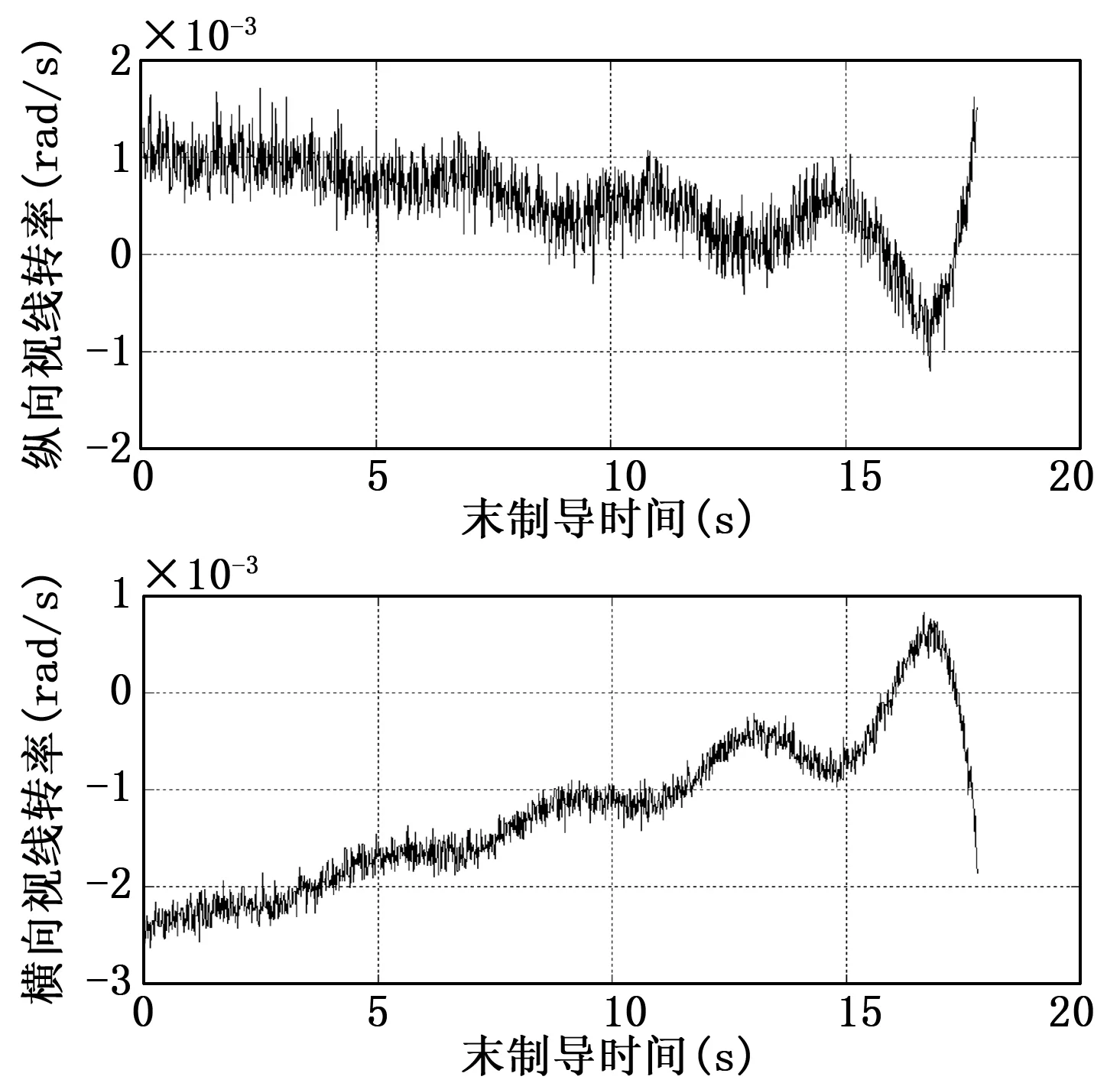
图4 视线转率的仿真曲线

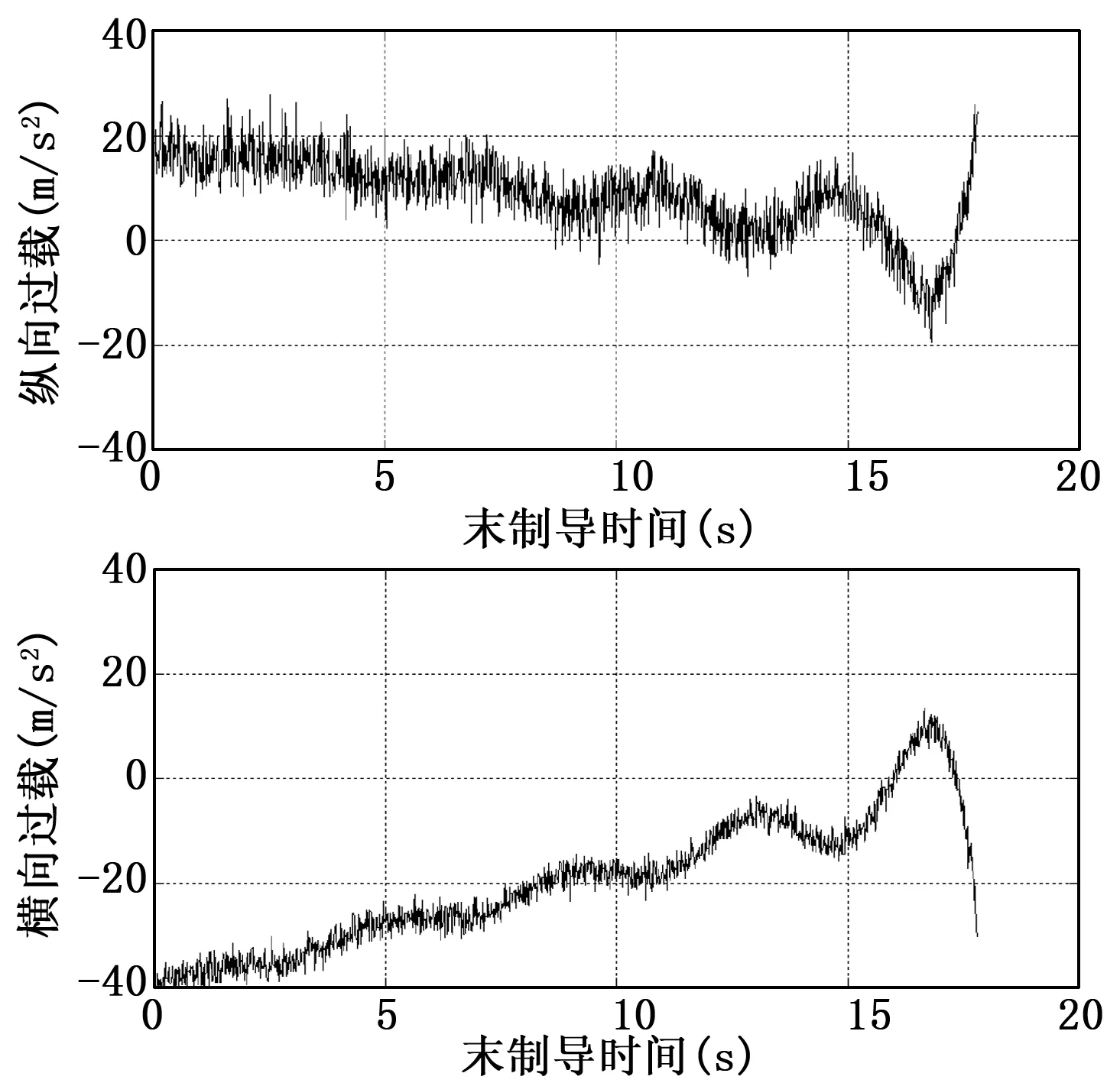
图5 过载的仿真曲线

可以看出，由于初始对准误差的存在，拦截器与目标之间存在较大的视线转动，造成零时刻指令过载较大，横向过载甚至接近饱和，随着拦截器与目标的不断接近，初始对准误差因此的视线转动逐渐被修正，目标的主动机动成为了造成视线转动的主导因素，过载指令也随之呈正弦型波动。

整个末制导过程中，纵向视线转率被控制在±2×10-3rad/s之间，横向视线转率被控制在±1×10-3rad/s，虽然在最后受到目标机动的影响较大，但指令过载并未达到饱和。

3.3.5 命中率和剩余质量估计

采用蒙特卡洛方法[13]测试“标准-3”拦截弹在当前场景的拦截效果，重复打靶试验100次，按照下式计算拦截器指令过载置零后的脱靶量：

可以得到零控脱靶量和拦截器剩余质量的分布如图6所示。

图6 蒙特卡洛打靶实验结果

当脱靶量为5 m以下时，认为拦截器命中目标，读取结果数据，可知“标准-3”拦截弹在场景中的命中率为89%，平均剩余质量为14.03 kg。

4 结论

本文基于美国的“标准-3”拦截弹的性能参数建立了数学模型，采用自适应滑膜制导律对大气层外机动目标的顺轨拦截过程进行了仿真研究，得到了以下结论：

1)采用“标准-3”拦截弹对大气层外机动目标进行顺轨拦截在时间和空间上是可行的，顺轨拦截方法具有较高的工程实践意义。

2)在考虑初始对准误差，视线测量误差，过载约束和动力学延迟的情况下，顺轨拦截方法对正弦机动的目标具有较好的防御效果，命中率约为89%。

3)仿真实例中拦截器的燃料消耗约为2.7 kg，指令过载在大部分时段内高于25 m/s2，考虑到安全裕度，若想对大范围强机动目标进行有效拦截，需要对现有拦截器的装药比和发

动机进行调整和改进。

[1] 刘燕斌, 南英, 陆宇平. 弹道导弹突防策略进展[J]. 导弹与航天运载技术, 2010(2):18-23.

[2] Morgan R, Vincent T, Cottrell R. Minimizing maneuver advantage requirements for a hit-to-kill interceptor[J]. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2013, 219(2):113-129.

[3] Nikos Mastrodemos, Daniel G. Kubitschek, Stephen P. Synnott. Autonomous Navigation for the Deep Impact Mission Encounter with Comet Tempel 1[J]. Space Science Reviews, 2005, 117(1-2):95-121.

[4] 谷志军, 陈 磊. 大气层外动能拦截器顺轨拦截技术研究[J]. 宇航学报, 2007, 28(5):1195-1198.

[5] Golan O, Shima T. Precursor Interceptor Guidance Using Sliding Mode Approach[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit. 2005.

[6] 高 乾, 周 林, 王云鹏,等. 大气层外动能拦截器顺轨拦截制导律设计[J]. 导弹与航天运载技术, 2011(6):1-5.

[7] 周 荻. 寻的导弹新型导引规律[M]. 北京：国防工业出版社, 2002.

[8] 陈 健, 孙 媛, 滕克难. 动能拦截导弹弹道数据计算研究[J]. 战术导弹技术, 2015(1).

[9] 胡泽保, 张振鹏. "标准-3"拦截导弹发动机参数复原设计[A]. 中国宇航学会固体火箭推进专业委员会年会[C]. 2004.

[10] Hablani H B, Pearson D W. Miss Distance Error Analysis of Exoatmospheric Interceptors[J]. Journal of Guidance Control & Dynamics, 2011, 27(2):283-289.

[11] 张涛涛. 大气层外拦截弹末段制导控制精度分析[D]. 北京：国防科学技术大学, 2012.

[12] 张 兵. 大气层外动能拦截器末制导段性能研究[D]. 北京：国防科学技术大学, 2005.

[13] 康崇禄. 国防系统分析方法[M]. 北京:国防工业出版社, 2003.