基于量子粒子群优化的表面波特征方程的数值求解

汪涛 国家新闻出版广电总局724台

1 前言

电介质波导和旋磁波导中非线性电磁动力学波的传播行为已经成为物理学、通信与信息科学领域中重要的研究课题.其理论和应用研究已成为现代高科技发展的巨大推动力。表面波波导这类传输线既可用在波长较长时（如米波），也可用在相当短的波长（如毫米波）。表面波传输线横向尺寸不大，因而有广泛的实用价值。微波集成电路技术亦需要表面波理论。正如“表面波”一词所表示的那样，它是一种沿两媒质之间的界面传播的电磁波，媒质之一通常是空气。界面可以是光滑表面（平面或曲面），也可以是周期性或不规则结构。表面波比光速慢，在界面处近距离上携带了大部分能量。表面波一般作为被导波而加以研究，但当它在传播过程中遭遇不连续性障碍时，或在专门的表面波天线设计中，它是辐射性的。实际上，分析介质导引的表面波关键是求解其特征方程。当介质为有耗时，该特征方程为一复超越方程，数值求解具有相当的难度。

量子行为粒子群算法（QPSO）是一种的能保证全局收敛的粒子群算法，QPSO算法把所求的问题对应于搜索空间中一个“粒子”。每个粒子都有自己的位置，还有一个适应值。各个粒子记忆，追随当前的最优粒子，在解空间中搜索。QPSO算法参数个数少，且进化方程的形式简单，更容易控制，运算速度快，精度高，占用资源少。

为此，本文应用量子粒子群优化算法对同轴馈电微带天线表面波特征方程进行了精确的数值求解。

2 量子粒子群优化算法（QPSO）

2.1 粒子群优化算法（PSO）

粒子群优化算法(PSO)是一种再现群智能的全局优化算法，它是从动物群体的觅食行为中受到启示，在群体搜寻最优目标时，每个个体在自己寻找目标的同时参照当前群体中其它最优个体达到的最优位置而调整下一步的搜寻。该算法采用速度－位置搜索模型，基本PSO算法公式描述如下：

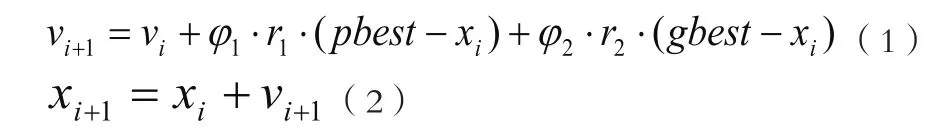
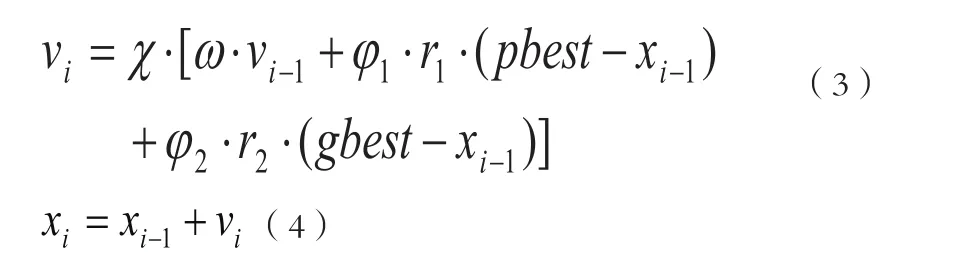
2.2 量子粒子群优化算法（QPSO）

根据粒子群的基本收敛性质，受量子物理基本理论的启发，Sun等人提出的QPSO算法是对整个PSO算法进化搜索策略的改变，并且进化方程中不需要速度向量，且进化方程的形式简单，参数少，容易控制。

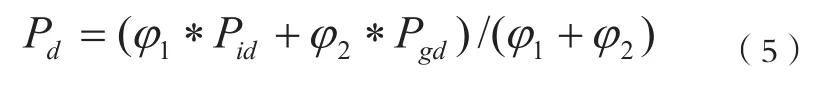
其 中 ϕ1=rand(0,1)， ϕ2=rnad(0,1)或 者Pd=ϕ∗Pid+(1 −ϕ)∗Pgd，0＜ ϕ ＜1。 全 局 点mbest来计算粒子的下一迭代步的变量L，它定义为所有粒子的局部最好位置的平均值公式如下：

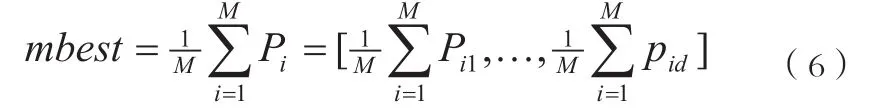
其中M是粒子的个数，iP是粒子i的局部最好位置。于是粒子的迭代方程为：

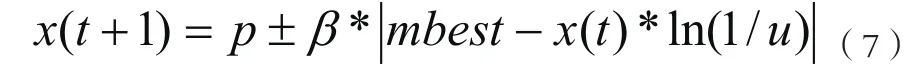
其中 )1,0(randu= ，β被称为收缩扩张系数，调节它的值能控制算法的收敛速度。一般而言β值在算法运行是从1.0线性减小到0.5时，可以达到比较好的效果，即：

其中MAXITER是迭代的最大次数。式(7)被称为具有量子行为的粒子群算法(简称QPSO)。

3 表面波特征方程的求解

下面研究微带天线表面波电磁场表达式及其特征方程的求解。

3.1 微带天线表面波电磁场表达式

微带天线贴片端口除了激励起空间辐射波外，也在介质基片上激励起表面波。在远离探针的区域，由于辐射波能量衰减比表面波快，可以近似认为只存在表面波。这种表面波是柱面波，且具有轴对称性，因而采用圆柱坐标系。空气中的表面波电磁场分量为：

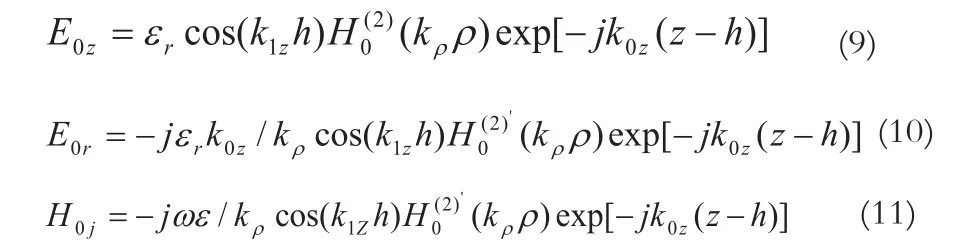
介质中的表面波电磁场分量为

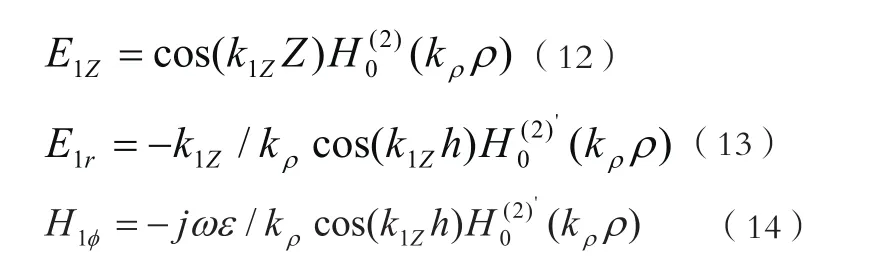
其中，式（9）-（11）中的 z＞ h；式（12）-（14）中的z＜h；er和µr分别为相对介电常数和相对磁导率；e0和µ0分别为真空中的介电常数和磁导率；h为微带天线的介质基片的厚度；分别为第二类Hankel函数及其导数。波数 k0z和 k1z满足的特征方程为：

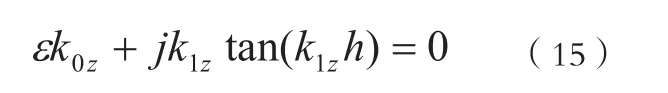
k0z，k1z和kρ之间有如下关系：

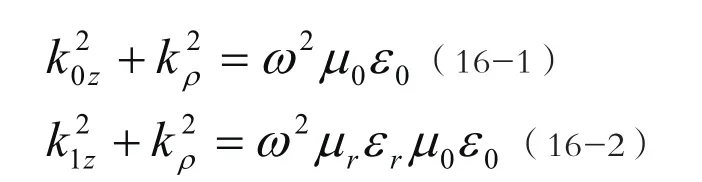
将式（15）和式（16）代入方程（9）-（14）便可得相应区域的电磁场分布。

3.2 表面波特征方程的求解

对于有耗介质平面上的微带天线表面波特征方程(15)，令 hkzz1= ，并考虑到方程（16），可以得到表面波特征方程为：

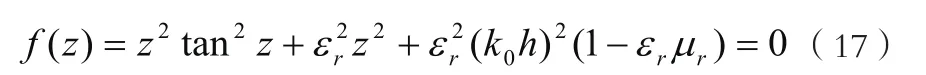
在高等电磁场领域，准确，快速的解此类复超越方程是个关键。

量子粒子群优化算法（QPSO）具有较好的全局搜索能力，利用此算法求解此表面波特征方程时，把待求的参量z看做搜索空间的粒子，粒子在搜索空间中找到的最优位置即为方程（17）的精确解。

4 结论

表面波是一种沿两媒质之界面传播的电磁波。本文提出利用量子粒子群忧化算法（QPSO）进行表面波特征方程的求解。使得求解速度快，精度高，且能节省大量的计算机内存。这为电磁场其他方程的求解奠定了基础。量子粒子群优化算法属于智能算法，智能算法广泛的应用于各个领域。电磁场中涉及的方程很多，如果能将智能算法正确的应用于此，则会在电磁场方面有一个突破。尤其是对于那些像超越方程等无法用常规算法解决的问题，均可用智能算法进行求解。

[1]钟顺时.微带天线理论与应用[M].西安电子科技大学出版社，1991

[2]龙云亮，蒋鸿雁.有耗介质平面上表面波特征方程的数值解[J].中山大学学报，1997，36（4）：27-30