基于BP神经网络系统的电力系统负荷预测
2018-02-05王善磊河海大学能源与电气学院
王善磊 河海大学能源与电气学院
电力系统的一项十分重要的日常工作便是电力系统负荷预测,负荷预测是否精准关系到电网运行的经济性、安全性以及电能质量。准确的电力负荷预测有助于合理地布局电力投资、统筹安排购电计划和制定运行时间,对于社会效益和经济效益的提升大有裨益。
早期研究的电力负荷预测方法主要有时间序列、回归分析、和趋势外推等 ,这些模型多基于线性建模,却未考虑到短期电力负荷预测受到天气、季节、节假日和经济等多种因素影响,忽略了负荷变化具有随机性、自相似性、突发性、混沌性的特点,从而导致预测结果与实际需求有一定的差距。
在此背景下,区间预测方法逐步受到重视。但是,区间预测不可避免的存在计算复杂、假设性强、预测时间长等问题,随着Eberh博士和kennedy博士粒子群算法的提出,在此理论支持下,基于粒子群群算法的电力系统负荷预测逐渐成为研究热点。文献[2]同样在粒子群算法的基础上,提出一种改进粒子群-c神经网络模型的短期电力负荷预测,通过神经网络模型的学习能力对电力系统负荷作出合理的预测。
BP神经网络良好的非线性处理能力,使得 BP神经网络结构变得更为简单、运算速度加快,提高了预测精度。笔者将通过实例对此说明。
1 BP神经网络算法的改进
1.1 传统的负荷预测过程:
对于基于BP神经网络的电力系统负荷预测模型,需要指出的是,传统理论上的BP网络模型在电力系统符合预测中存在着以下问题:学习时间过长,学习效率低下。电力系统的负荷预测较其他问题而言相对复杂,传统的学习方式效率低下;基于传统BP神经网络的负荷预测,难以满足目标精度。
因此需要对该理论模型进行改进,笔者主要从以下三个方面进行了改进:
1.2 BP网络模型的改进
1.2.1 利用动量法调整权值
权值得选取是BP神经网络系统的核心,文章采用动量法权值调整法对权值做出如下计算:
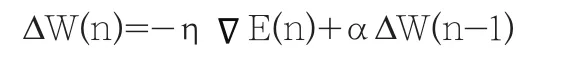
其中:α为动量系数,通常0<α<0.9;η—学习率,范围在0.001~10之间。
这种做法就是上一次权值调整量的一部分迭加到按本次误差计算所得的权值调整量上,作为本次的实际权值调整量。这样做的原因是电力系统的负荷前后具有一定的关联,相互影响,因此须在此对BP算法进行一定的改进。
另外,所加的动量因子其实相当于阻尼项,有效抑制了了学习过程中的振荡趋势,从而改善了收敛性。大大降低了网络对于误差曲面局部细节的敏感性,同时又能做到预测值之间的相互关联。
1.2.2 采取自适应方法调整学习速率
学习率选择不当对于电力系统负荷预测的精准度以及预测效率都有一定的影响。学习率取值太小,收敛过慢,预测效率低下学习率选得太大,修正过头,产生振荡甚至发散。因此文章将改进学习率:在学习收敛的情况下,增大η,以减少学习时间;当η偏大甚至不能收敛时,要适当减小η,使其合理收敛。
1.2.3 学习规则调整
Levenberg-Marquardt算法比较而言运算速度快,算法结构简单,虽然需要相当大的存储空间,但整体而言还是拥有较高的选择权。其对于权值的调整有如下规定:
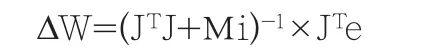
2 实验验证
2.1 改进的BP网络模型效果验证
为了验证所改进模型的正确性,笔者通过具体的仿真实验,通过调取某日某市的负荷数据,设置12个节点进行仿真,设定预期目标ε=0.0001。
2.2 对比结果分析
传统的BP网络模型不仅学习速度上较慢,最终结果的精度也难以达到要求。反观改进后的BP网络模型,其训练误差达到9.89028×10-5,测试误差为1.9899×10-4,符合预期的目标。
3 结束语
文章通过对现有的BP网络模型进行研究,找出其不足之处,并结合电力系统负荷预测的需求,将模型进行了改进。最后通过实验证明,改进后的神经网络模型不仅在学习速度上有所改观,最终的精度也能达到预期要求。这对于今后的电力系统负荷预测,具有较高的参考价值。
[1]朱继萍,戴君.中长期电力负荷预测相关影响因素优化选择[J].计算机仿真,2008,25(5): 226-229.
[2]雷绍兰,孙才新,周湶,等.电力短期负荷的多变量时间序列线性回归预测方法研究.中国电机工程学报,2006;26(2):25—29
[3]赵宏伟,任震,黄雯莹.基于周期自回归模型的短期负荷预测.中国电机工程学报,1997;17(5):350—353
[4] 林晓华,冯毅雄,谭建荣.基于免疫优化的产品系统可靠性参数区间预测方法[J].浙江大学学报(工学版),2013,(6):1013-1021
