基于GM(1，1)残差修正模型的飞行训练量预测

姚裕盛，徐开俊，杨 泳

(中国民用航空飞行学院 飞行技术学院，四川 广汉 618307)

0 引言

自20世纪60年代以来，全世界民用航空产业持续高速发展，我国民航事业的发展也取得了令人瞩目的成就。如此快速的发展无疑给我国的民航飞行员培养带来了新的机遇和挑战，各个飞行训练机构每年都承担着巨大的飞行训练任务。由于飞行训练的开展受到很多因素的制约，比如天气环境的影响，各个季节气候的影响，还可能出现一些无法预期的突发状况打乱飞行计划。所以各年份的训练量会呈现一定的波动性和不确定性，因此做好阶段性的训练容量预测也就显得尤为重要，准确的对训练量进行预测有助于制定合理的飞行计划，安排合适的训练任务，对提高飞行训练的效率有很大的帮助。

预测是对尚未发生或目前还不明确的事物进行预先的估计和推测，如果能够实现准确的预测就能更好的做计划安排，对事物有一个宏观的把握。预测方法基本可以分为定性预测和定量预测两大类，随着研究的不断深入，科技的持续发展，预测的方法经历了一个发展完善的过程。从传统的时间序列预测方法，到不断出现的一些新的预测方法，比如灰色预测理论，人工神经网络，支持向量机以及遗传算法等，通过引入复杂人工智能的方法来突破传统预测方法的局限性。

时间序列分析预测法作为传统的预测方法，它是根据过去的变化趋势预测未来的发展。它充分考虑了预测对象过去和现在的变化规律，对于短、近期的预测比较显著，但是忽视了外界各种不确定因素的影响[1]，这也势必会导致预测结果在一定程度上的不准确。自我国邓聚龙教授提出灰色系统理论之后，经过多年的发展，该理论已经在各个邻域得到了广泛的应用。清华大学的何国华利用灰色预测模型进行区域物流需求预测[2]，结果表明灰色预测模型对数据要求限制少、中短期预测精准等特点，特别适合区域物流需求的预测。焦文玲等人根据灰色理论与灰色预测的原理，对城市燃气负荷进行预测[3]，并进行了实际的应用。张雅君、刘全胜从灰色模型的特点与需水量本身的变化规律出发，揭示了模型的应用条件及其在需水量预测中的应用范围，并对北京市需水量进行了灰色预测[4]。吴强等人将灰色预测法应用在城轨客流预测中[5]，提出了在预测过程中数据的维数以及连续性问题。中国民航大学的潘毅志将灰色预测算法应用到近空域的空中交通流量预测[6]，研究表明相对于传统线性预测方法，灰色预测可以将目标函数曲线与预测函数曲线更好地进行拟合。另外付建飞、安仲文等基于灰色模型对铁路分品类货运量进行预测[7]，同时还介绍了检验模型的方法。由此可见灰色预测模型在各个领域都得到了广泛的应用，而且都取得了很好的效果，主要是因为灰色预测模型所需样本数据少，不用考虑数据的分布规律以及变化趋势，建模简单，运算方便，因此应用广泛。

本文就是在传统灰色预测的基础上，建立残差修正模型，对某飞行学院的飞行训练量进行预测，验证了模型的有效性，且比较模型之间的预测精度，结果表明改进后的灰色预测模型对现有的数据进行预测，具有更高的预测精度。

1 灰色预测模型

灰色系统理论的实质是将无规律的原始数据进行累加生成，得到规律性较强的生成数列后再重新建模。它实际上是一种以数找数的方法，从系统的一个或几个离散数列中找出系统的变化关系，试图建立系统的连续变化模型。灰色问题建模使用最多的是GM(1,1)模型，其建模过程如下：

假设有时间序列

(1)

X(1)为X(0)的一阶累加生成序列：

(2)

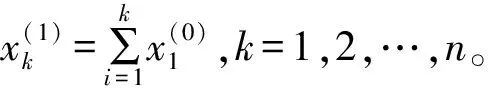
累加生成的数列可以使任意非负数列变为非减的递增数列，这样使该数列的随机性得到减弱，规律性得到加强[8]。

构造一阶微分白化方程：

(3)

式中，a称为发展灰数，反映X(1)及原始序列X(0)的发展趋势；b称为内生控制灰数，反映了数据间的变化关系。

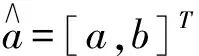
(4)

令

(5)

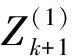
假定b取值为0.5，则有：

(6)

将式(3)离散化后，则有：

利用最小二乘法求解参数：

[a,b]T=(BTB)-1BTY

(7)

式中，

假定x(1)=x(0)，解微分方程(3)得到响应函数：

(8)

(9)

2 预测模型精度检验

一般采用后验差检验对模型得到的预测结果的拟合效果进行评价，检验预测模型的精度。后验差检验包含两个值的计算[9]，一个是后验差比值，另一个是小误差概率。计算过程如下：

计算原始序列标准差：

(10)

计算绝对误差序列的标准差：

(11)

计算后验差比：

(12)

计算小误差概率：

(13)

后验差比C越小，小误差概率P越大时，预测精度越高，计算精度等级[10]参考表1。

表1 灰色预测模型精度检验等级表

如果经过精度检验发现预测效果不好时，需要对原模型进行改进，以期提高预测精度。

3 基于GM(1,1)的残差修正模型

以上GM(1,1)模型应用在波动的原始数据类型，造成最后的预测精度较低，所以在传统模型的基础上进行改进，采用一种残差修正的灰色预测模型，它的理论实质就是将GM(1,1)模型生成的残差数列再进行一个灰色预测，最后的预测值即为两次预测值的相加，引入残差修正可以提高预测精度。残差修正模型建模过程如下：

将之前灰色预测模型中(9)式得到的预测值代入(14)中得到残差序列E(0)。

E(0)=(e(0)1,e(0)2,…,e(0)k)

(14)

如果得到的残差序列E(0)中的元素有负值则需要根据式(15)进行正化处理，得到序列F(0)：

(15)

(16)

残差模型一般只注意修正原点附近的数，而不是修正所有的数，只选用最后残差较大的值构成残差尾段序列q(0)建模，然后根据试(15)进行正化处理后得到残差尾段Q(0)。

(17)

利用得到的新的序列Q(0)作为原始序列按照之前的(1)～(9)式进行GM(1,1)建模。得到残差模型为：

(18)

(19)

利用得出的残差模型对原模型进行修正可得基于GM(1，1)的残差修正模型值：

(20)

4 模型应用

中国民航飞行学院的飞行训练，作为一类特殊的本科教学，每年承担着2500～3000人次的飞行学员训练任务，每年超过20多万小时飞行训练量。而且训练量呈现出逐年缓慢增长的一个趋势，如图1，是该学院2009年～2015年全年训练总量增长情况。训练计划的有效制定和实施是保证高效训练的必要前提，所以必须对每年的训练量情况全面的了解。该学院下面有五个分院进行飞行训练，本例选取其中的广汉分院作为研究对象，对它的训练量进行预测。图2是广汉分院2009年～2016年每年3月～11月训练量的变化情况。

图1 全年训练量变化曲线

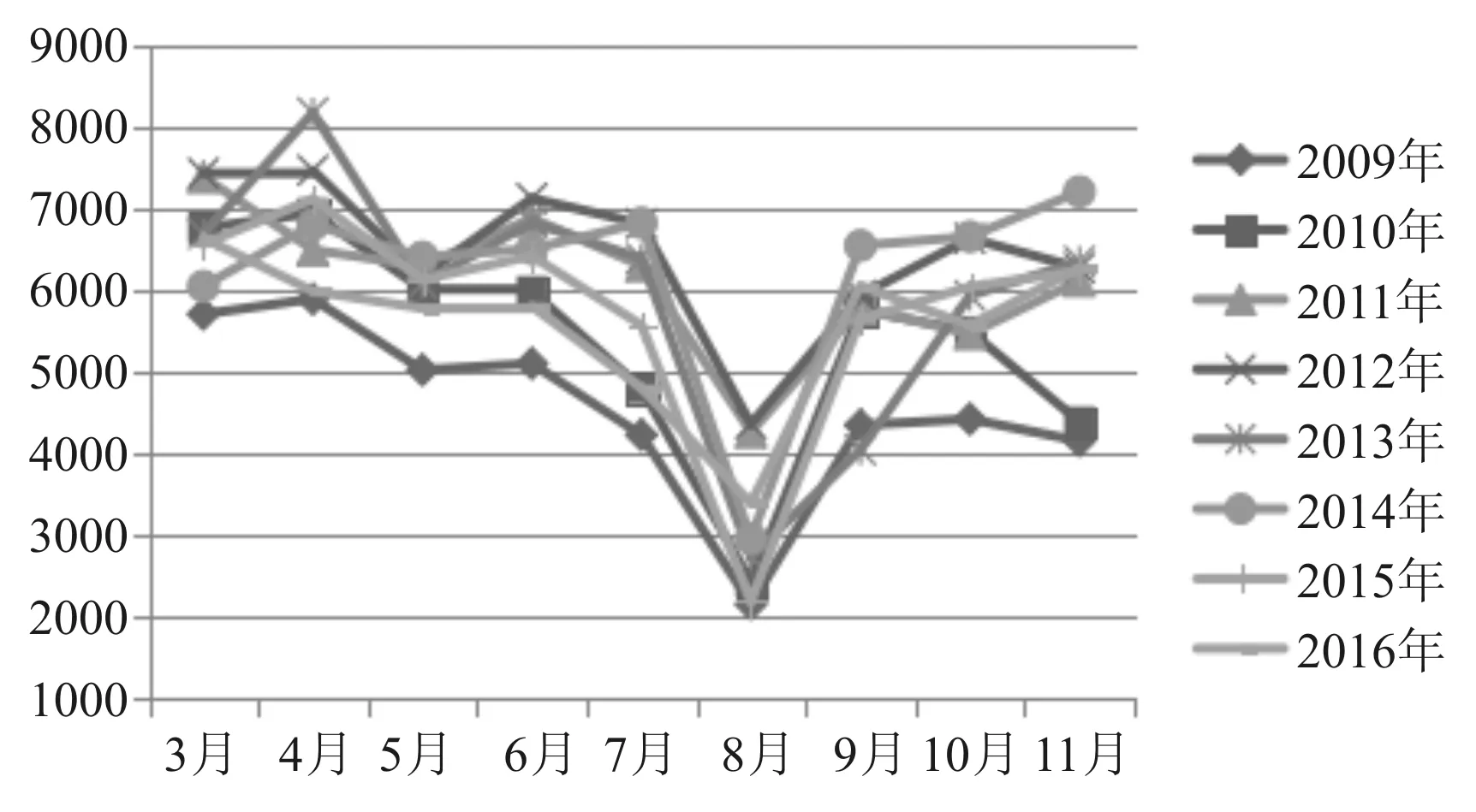
图2 全年各月训练量变化曲线

从图2可以看出每年当中各月的训练量存在很大的差异，但是总体来看是呈现出一定的变化趋势的。所以对训练量进行科学的预测很有必要。预测的主要过程是：将2009年～2015年的训练量作为原始数据对2016年3月到11月的训练量进行预测，由于各月波动性很大，而相同的月份的训练量比较集中，所以预测时是利用2009年～2015年3月训练量预测2016年3月的训练量，如此重复进行9次预测就得到了2016年3月～11月的训练量预测值。

以2016年5月的训练量预测为例，具体过程如下：

取2009年～2015年3月的训练量数据进行建模，得到原始序列：

X(0)=(5015.6，6004.3，6283.2，6163.9，6069.4，6398.8，6123.9)

对原始序列进行一阶累加生成得到累加生成序列为：

X(1)=(5015.6,11019.9,17303.1,23467,29536.4,35935.2,42059.1)

由(7)式可得：a=-0.00391，b=6082.13。

由(8)可得时间响应函数为：

根据式(9)可以得到GM(1,1)模型的预测值：

n

经计算得到预测值序列：

X(0)=(5015.6,6113.6967,6137.6566,6161.7104,6185.8585,6210.1012,6234.4389)

残差序列：

E(0)=(0,-109.3967,145.5434,2.1896,-116.4585,188.6988,-110.5389)

根据式(10)～(13)计算得到：P=1,C=S2/S1=162.89434/457.31779=0.3562。参照表1可知此模型应用在该数据上精度不是特别高，所以在此基础上利用残差修正模型进行改进，提高预测精度。

利用残差修正模型改进，预测过程如下：

取残差尾段：q(0)=(-109.3967,145.5434,2.1896,-116.4585,188.6988,-110.5389)，对其进行正化处理得到：Q(0)=(123.520,378.460,235.107,116.458,421.616,122.378)。

将Q(0)作为原始序列重复(1)～(8)式过程进行GM(1,1)建模，计算得到残差模型响应函数为：

根据(19)、(20)式最终得到基于GM(1,1)的残差修正模型：

将数值代入上式就可以得到最终的预测值为：

对最后的预测结果进行残差检验：P=1，C=0.3459。参照表1可知所建的残差模型等级为好，该模型可以进行训练量的准确预测。

取k=7，代入残差修正模型就可以得到2016年5月的训练量预测值为6172.145小时。

2016年其他各个月的训练量通过重复以上过程进行预测，最后得到的传统灰色预测值以及基于GM(1，1)残差修正模型预测值整理如表2。

表2 2016年训练量预测值

得到的预测效果如图3所示。

图3 2016年各月训练量预测效果

5 结语

从表2以及图3可以分析出，利用传统灰色预测模型对波动比较大、没有稳定缓慢增长趋势的数据应用预测效果不佳，存在很大的误差，但是经过残差修正后的模型能够很好的弥补这个缺陷，达到预期的预测效果。通过最后的预测值和实际训练量的比较，可以看出，文中经残差修正后的GM(1,1)模型能够有效地对该飞行学院的训练量进行预测，科学的预测方法可以对该学院制定合理的训练计划，科学的安排训练任务有很大的辅助作用。当然，这种模型得到预测值和实际训练量还存在一定的误差，有待今后的进一步改进和完善。

[1] 徐国祥.统计预测和决策[M].上海:上海财经大学出版社,2005:35-36 .

[2] 何国华.区域物流需求预测及灰色预测模型的应用[J].北京交通大学学报(社会科学版),2008,7(1):33-37.

[3] 焦文玲,严铭卿,廉乐明.城市燃气负荷的灰色预测[J].煤气与热力,2001,21(5):387-389.

[4] 张雅君,刘全胜.城市需水量灰色预测的探讨[J].中国给水排水,2002,18(3):79-81.

[5] 吴强,冯维琇,胡晓嘉.灰色预测法在城轨客流预测中的应用[J].城市轨道交通研究,2004,7(3):52-55.

[6] 潘志毅. 空中交通流量的灰色预测方法应用[J].科技信息,2011(18):527.

[7] 付建飞,安仲文,宋小满,等.基于灰色模型的铁路分品类货运量预测[J].交通运输工程与信息学报,2014,12(3):38-42，46.

[8] 马晓光,孟伟.残差修正法在电力负荷预测中的应用[J].电网技术,2001,25(4):21-23.

[9] 李论. 基于灰色预测模型的我国心脑血管疾病死亡率预测[J].现代电子技术,2015,38(11):107-111.

[10] 陈新国,訾丽.基于残差修正GM(1,1)模型的年降水量预测研究[J].水资源研究,2014,35(4):4-6.