两级式逆变器母线电压二次纹波分析及抑制
2018-02-03袁义生张育源钟青峰胡根连
袁义生,张育源,钟青峰,胡根连
(1.华东交通大学电气与自动化工程学院,南昌330013;2.国网南昌供电公司,南昌 330012)
两级式逆变器[1-6]已广泛应用于航空静止变流器、车载逆变电源、光伏并网逆变器等。由于逆变器输出的电压和电流都是交流电,使得输出的瞬时功率中除了有直流分量外还含有2倍频的脉动功率,而系统的输入功率是直流量,这就造成输入输出功率的不平衡。中间直流母线电容作为两级式逆变器前级和后级的解耦电容,承担了系统中存在的2倍频脉动功率,从而使得母线电容电压中含有二次低频电压纹波。中间母线电容一般会选择电解电容,而电解电容使用寿命短且承受纹波的能力很小,较大的低频电压纹波会引起母线电容发热从而进一步危及母线电容的运行寿命,进而危及整个逆变器的使用寿命。此外,较大的低频电压纹波对系统造成的影响还有:影响DC/AC级的交流输出效果,使输出电压波形削顶而产生畸变;影响系统的动态性能。因此,研究抑制两级式直交逆变器中间母线电容低频电压纹波的方法具有实际意义。
文献[7]提出用加大中间母线电容的方法抑制两级式逆变器母线电容低频电压纹波,这相当于增加了前级DC/DC变换器的输出滤波电容,只能在一定程度上减小母线电压低频纹波,当电容增大至一定值时,不仅母线电压低频纹波抑制效果有限,还会降低DC/DC变换器的动态响应速度,增大系统的体积、重量,使逆变器的可靠性降低;文献[8]提出用增大母线电压平均值的方法减小母线电容电压低频纹波,这使得系统中器件承受的电压应力增大,对器件的选型造成困难,而且中间直流母线电压的增大还会使得逆变器调制比减小,进而影响系统的效率;文献[9]提出在中间直流母线上并联功率解耦变换器的方法以抑制母线电容低频电压纹波,引入的功率解耦电路使得系统结构及控制变复杂、成本提高,而且由于脉动能量始终在功率器件中流动,变换器的转换效率较低;文献[10]提出了减小DC/DC变换器中纹波占空比波动的方法以抑制直流母线电容上低频电压纹波,该方法的不足之处是需要额外增加精确的电流传感器,增大了系统的成本;文献[11]提出了改变前级直流变换器外环电压控制器参数的方法以增大前级电路电压环截止频率从而达到抑制中间母线电容低频电压纹波的目的。但是这个方法需要精心计算电压环截止频率与该纹波电压之间复杂的关系,截止频率会受到电流环控制器的限制,且未提供这种方法下的动态特性;文献[12]提出了在前级电压环给定上注入一个与母线电压同频、同相的二次谐波扰动量的方法,通过调节扰动量的大小以达到减小母线电压低频纹波的目的。
本文提出了一种输出功率前馈的方法,即用瞬时输出功率除以输入电压得到一个电流信号,再将此电流信号叠加到前级直流变换器电流环的给定信号处,以达到减小母线电容二次电压纹波的目的。所提出的控制方法不需要额外增加辅助硬件,仅通过改变控制算法就可实现母线电压二次纹波抑制。系统采用DSP全数字化控制,因此,所提出的控制方法实现起来比较简单。仿真和实验结果验证了所提出的控制方法的正确性和有效性。
1 两级式逆变器工作原理
本文研究的两级式逆变器拓扑结构如图1所示,其前级采用Boost电路,后级采用单相全桥逆变电路。图中:Q1~Q5为功率开关管,Cdc为中间母线电容,L为前级Boost电路升压电感,D为二极管,Lo和Co分别为两级式逆变器输出滤波电感和输出滤波电容,Zo为两级式逆变器所带的负载,uo和io分别为两级式逆变器瞬时输出电压和瞬时输出电流,iinv为后级逆变器瞬时输入电流,ic为中间母线电容瞬时输入电流。两级式逆变器前后级各自的作用为:前级Boost电路用于升压完成逆变器输入输出之间的电压匹配,后级全桥逆变电路用于完成直流到交流转换,得到的交流电用于给终端负载供电。

图1 两级式逆变器拓扑Fig.1 Topology of two-stage inverter
假设两级式逆变器的瞬时输出电压uo和输出电流io均为理想正弦波形,两级式逆变器所带的负载Zo为线性负载,则两级式逆变器的瞬时输出功率po(t)的表达式为

其中

式中:Uo和Io分别为两级式逆变器瞬时输出电压和电流的幅值;ωo和fo分别为输出电压的角频率和频率;φ为负载阻抗角。
由式(1)可知,两级式逆变器的瞬时输出功率包含直流分量和2倍输出频率脉动分量,该脉动分量将造成交流输出侧波动的瞬时功率与直流输入侧功率无法实时匹配,从而使中间母线电容Cdc上含有二次低频电压纹波。正是由于Cdc的存在,前后两级可以分开分析和建模,独立控制。
由于母线电容一般较大,母线电容电压中二次电压纹波比例较小。假设中间直流母线电压udc的平均值为Udc,且忽略系统损耗,则根据能量守恒定理,可推出在忽略高频谐波分量的情况下后级逆变器瞬时输入电流iinv(t)为
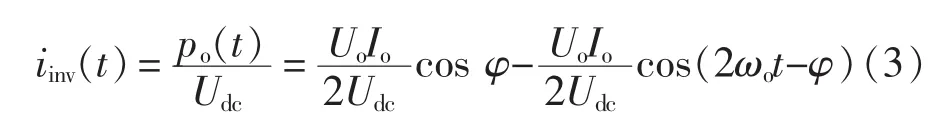
根据式(3),后级逆变器的瞬时输入电流由一个直流分量和一个二次纹波分量(2倍输出电压频率的交流分量)组成,其中,直流分量代表逆变器工作时消耗的有功功率。由于电容的隔直通交特性,后级逆变器瞬时输入电流中二次纹波分量将由中间母线电容Cdc提供。因此,中间母线电容瞬时输入电流ic(t)为

则中间母线电容二次电压纹波Δudc(t)为

可得中间母线电容电压udc(t)为

即母线电容电压可近似等效为直流分量与一个二次谐波分量的叠加。
2 中间母线电压二次纹波抑制
2.1 两级式逆变器控制策略
图2所示为本文研究的两级式逆变器控制策略框图,图中虚线框部分为本文提出的功率前馈控制方案,用于抑制其中间母线电压二次纹波。

图2 两级式逆变器控制策略框图Fig.2 Control strategy diagram of two-stage inverter
基于双环控制和数字控制技术的突出优点,此两级式逆变器前、后级系统采用的控制策略均为DSP实现的平均电流控制。在前级Boost升压电路中,外环电压给定信号Uref与母线电压采样信号udc相减所得误差信号经电压环调节器Gv(s)后产生电感电流指令信号i*L,电流内环则控制反馈的输入电感电流iL快速精确地跟踪给定电流i*L。
假设能量传输没有损耗,则根据能量守恒定理,可推出两级式逆变器的输入电流(即前级Boost变换器的输入电感电流)iL为

式中,Uin为两级式逆变器的输入电压。


因此,Uref-udc=0,从而推出udc=Uref。由此可知,中间母线电压udc仅含有直流分量Uref,而不含有二次纹波分量,从而达到了抑制母线电压二次低频纹波的效果。
2.2 前级直流变换器控制器设计
对Boost变换器运用小信号分析法可得其在电流连续模式下的小信号模型,如图3所示。

图3 Boost变换器小信号模型Fig.3 Small signal model of Boost converter
图中:D'=1-D=0.5,Uin=100 V,Cdc=1 290 μF,R= 24.2 Ω,Ls=1 mH。
根据小信号模型可推出Boost变换器在CCM下的相关传递函数。
(1)输入电感电流对占空比控制变量的传递函数Gid(s)为

(2)Boost变换器输出电压(即中间直流母线电压)对输入电压的传递函数Guu(s)为

(3)Boost变换器开环输入阻抗Zin(s)为

由式(11)和式(12)可得Boost变换器输出电压对输入电感电流的传递函数Gui(s)为
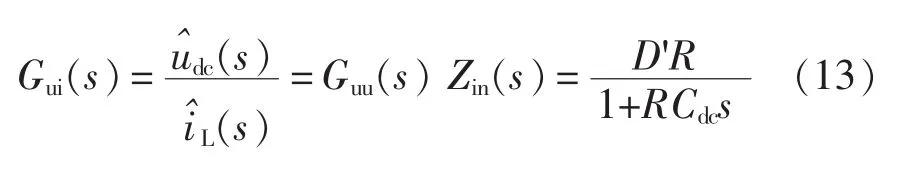
2.2.1 电流内环控制器设计
图4为电流内环的控制策略框图,其中,Fm(s)为PWM调制器增益,Fm(s)为0.5,fs为系统开关频率,取值100 kHz,电流环控制器Gi(s)采用单零点ωzi、单极点ωpi的补偿网络。Gi(s)表示为

根据多环控制理论的知识,电流内环的截止频率应远大于电压外环的截止频率,以使内外环互不影响,且电流环截止频率fci应足够大以改善动态性能,同时为避免高频开关纹波引入系统,通常fci<(1/2π)fs。控制器积分环节的作用是提高低频增益,消除稳态误差,保证静态性能;控制器零点用于保证系统在截止频率处相位裕量够大;高频段的极点用于保证系统在开关频率处有足够的衰减,提高系统抗高频干扰能力。基于以上设计原则,电流环控制器参数可取为ωzi=3 000,ωpi=739 000,Kpi=739 000,如此可得加入控制器补偿后的电流环开环系统伯德图,如图5所示。由图可知,加入补偿网络后的电流环,其截止频率为15.5 kHz,相角裕度为80°,这既能保证系统的稳定性,又能满足系统的响应速度。

图4 电流环控制框图Fig.4 Control block diagram of current loop

图5 电流内环开环频率响应Fig.5 Open-loop frequency responses of inner current loop
2.2.2 电压外环控制器设计
若电流内环控制反馈的电感电流iL能快速精确地跟踪指令电流i*L,则电流内环的增益近似为1,此时电压环控制框图可简化为图6所示,电压环控制器Gv(s)同样采用的是单零点ωzv、单极点ωpv的补偿网络,即

式中,Kpv为电流环比例系数。当电压外环的开环截止频率fcv设计得很低时(10 Hz左右),系统的响应速度慢,若逆变器负载进行投切载,则中间直流母线电压将出现较大波动。逆变器突然减载时,直流母线电压会有较大的升高,这会使系统中功率开关管承受的电压应力增大;逆变器突然加载时,直流母线电压会有较大的下降,再加上直流母线电压叠加了较大的二次低频电压纹波,很可能导致母线电压低于逆变器正常工作所需的最小直流母线电压,这将造成输出的电压电流波形出现削顶而产生畸变,导致逆变器不能正常工作。因此,低电压环截止频率时,系统容易受到干扰,其动态特性较差。为了解决系统响应速度慢而带来的问题,在设计电压外环的截止频率时应将其设计的大一些,以加快系统的响应速度,改善系统的动态性能。本文中电压环控制器Gv(s)的参数可设计为Kpv=720,ωzv=15,ωpv= 450,如此可得加入控制器补偿后的电压环开环系统伯德图,如图7所示。由伯德图可知,加入补偿网络后的电压环,其截止频率为72 Hz,相角裕度为48°,系统稳定。
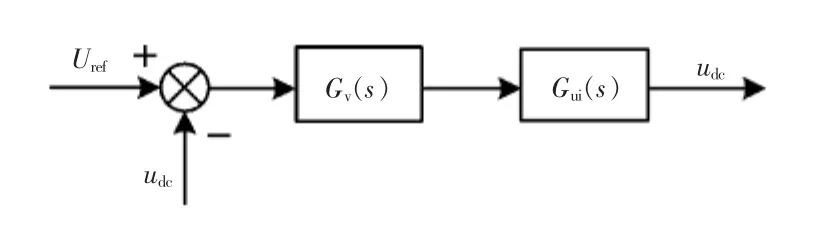
图6 电压环控制框图Fig.6 Control block diagram of voltage loop

图7 电压外环开环频率响应Fig.7 Open-loop frequency responses of outer voltage loop
2.3 单零点双极点控制器的数字化
由于DSP只能处理数字量,因此,在对Boost变换器进行数字控制时,需要对电压环、电流环的控制器进行数字化。电压环、电流环采用的单零点单极点补偿网络可用一般形式表示为

式中:e(s)为指令与反馈的差值;A、B、C和K为常数。
将式(16)进行反拉式变换,可得

采用离散化方法[13]可得
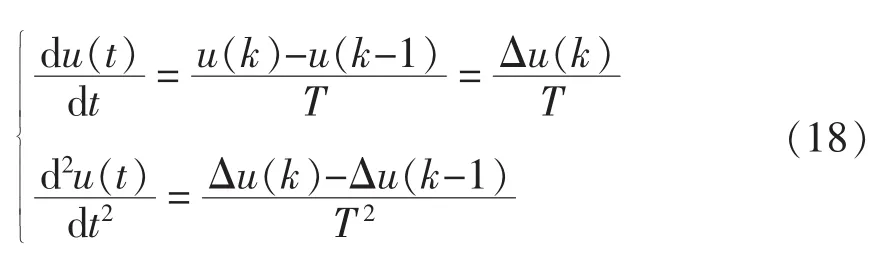
式中:K为开关次数;T为开关周期。将式(18)代入式(17),整理后可得

式(19)即为单零点双极点补偿网络增量式控制算法的增量部分。由式(19)可得便于DSP实现的增量式数字控制器的表达式为

3 仿真分析
为研究本文提出的输出功率前馈控制方案对两级式逆变器中间母线电压二次纹波的抑制效果,基于Saber软件搭建了两级式逆变器控制系统,系统参数如表1所示。仿真结果如图8、图9所示。图8为不同负载情况下未引入功率前馈时电路的仿真波形,由图可以看出,中间母线电压udc含有2倍逆变输出电压频率的低频脉动分量。图8(a)为两级式逆变器带R负载时的电路波形,逆变器输出电压、电流同相位;图8(b)为两级式逆变器带RL负载时的电路波形,相位上逆变器输出电压超前输出电流58.2°;图8(c)为两级式逆变器带RC负载时的电路波形,相位上逆变器输出电压滞后输出电流50.3°。图9为引入功率前馈时的电路仿真波形。从图9可看出:引入功率前馈后,对于R负载、RL负载、RC负载,中间母线电压udc的二次电压纹波都得到了抑制,且抑制效果明显。
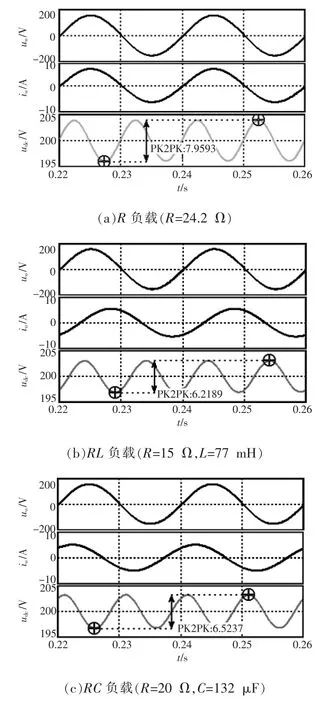
图8 未引入功率前馈时电路仿真波形Fig.8 Simulation waveforms of the circuit without power feedforward

图9 引入功率前馈时电路仿真波形Fig.9 Simulation waveforms of circuit with power feed-forward
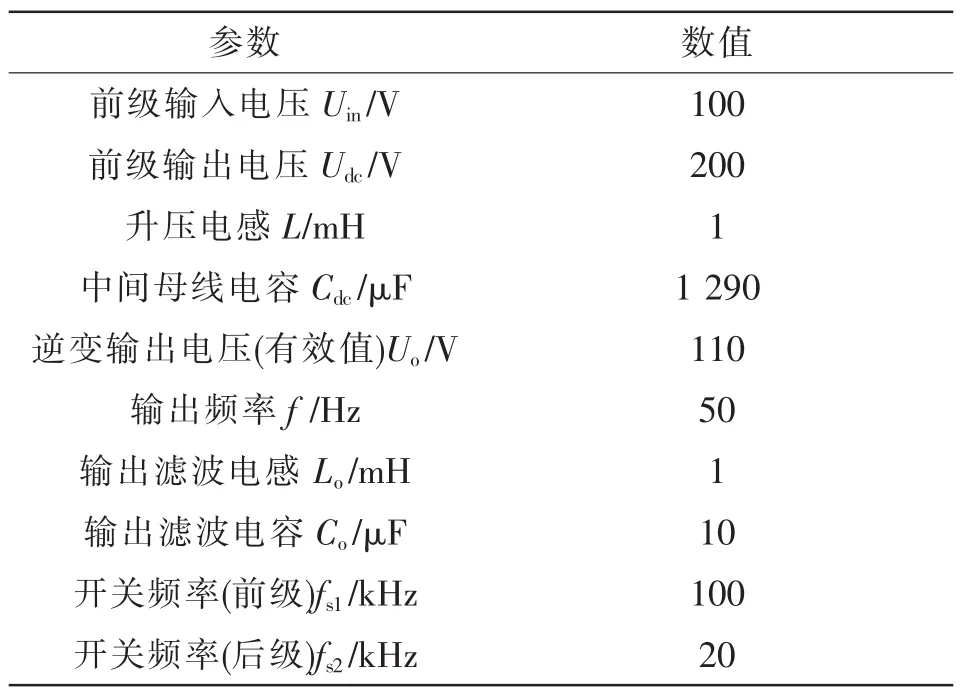
表1 两级式逆变器系统参数Tab.1 System parameters of two-stage inverter
4 实验分析
为了验证所提出的输出功率前馈控制方案抑制两级式逆变器中间母线电压二次纹波的正确性与有效性,本文研制了一台基于DSP F28335控制的500 W的两级式逆变器原理样机,实验主要参数如表1所示。图10为未引入功率前馈时电路的实验波形,图10(a)为两级式逆变器带纯电阻负载,图10(b)为两级式逆变器带的是非线性RCD负载,实验波形也证实了母线电压udc含有2倍逆变输出电压频率的低频脉动分量。图11为引入功率前馈时电路的实验波形。从图中可以看出,引入功率前馈后,不论是线性电阻负载,还是非线性RCD负载,中间母线电压的二次电压纹波均能得到很好的抑制。图12为引入功率前馈后逆变器带电阻负载时系统由半载到满载突变的动态响应波形图。由图12(a)可知,负载由半载到满载切换时,母线电压udc不仅有较大的波动,而且需经2~3个输出周期才能稳定,因此,低带宽时系统动态响应速度慢;由图12(b)可知,负载同样由半载到满载切换时,母线电压udc几乎没有波动,且能马上进入稳态,因此,较高的带宽可使系统动态响应速度加快,动态特性变好。

图10 未引入功率前馈时电路实验波形Fig.10 Experimental waveforms of the circuit without power feed forward

图11 引入功率前馈时电路实验波形Fig.11 Experimental waveforms of the circuit with power feed forward

图12 带电阻负载时系统动态响应波形Fig.12 System dynamic response waveforms with resistive load
5 结语
本文分析了两级式逆变器中间母线电压二次低频纹波的产生原因及母线电压低频纹波的计算方法。为了解决中间母线电容低频电压纹波带来的不利影响,本文提出了一种输出功率前馈的控制方法,给出了前级Boost变换器电流环、电压环的设计过程,并对双环控制中具有单零点双极点的补偿网络进行了数字化,得到了便于DSP实现的增量式数字控制器的表达式,搭建了两级式逆变器控制系统的仿真模型并研制了一台500 W的实验原理样机进行仿真和实验验证。仿真和实验结果表明:中间母线电压二次纹波得到了很好的抑制。对于中间母线电容二次电压纹波,所提出的控制方法不仅对线性负载(如R负载、RL负载、RC负载)具有良好的抑制效果,对非线性负载(如RCD整流性负载)同样具有很好的抑制效果,且当前级Boost变换器电压环的带宽设计的较大时,系统的动态性能在较大范围负载切换输出时是比较优良的。此外,所提控制方法在负载切换时同样能保证有效抑制中间母线电压低频纹波。由于仅通过DSP改变控制算法且没有在系统中增加辅助硬件,所以,该控制方法实现起来比较简单。
[1]邓翔,韦徵,龚春英,等.一种新颖的抑制两级式直交逆变器输入电流低频脉动的方法[J].中国电机工程学报,2011, 31(30):24-29.
Deng Xiang,Wei Zheng,Gong Chunying,et al.A novel technique for low frequency input current ripple reduction in two-stage DC-AC inverter[J].Proceedings of the CSEE, 2011,31(30):24-29(in Chinese).
[2]祝国平,阮新波,王学华,等.两级式单相逆变器二次纹波电流的抑制与动态特性的改善[J].中国电机工程学报, 2013,33(12):72-80,188.
Zhu Guoping,Ruan Xinbo,Wang Xuehua,et al.Suppression of the second harmonic current and improvement of the dynamic performance for two-stage single-phase inverters[J].Proceedings of the CSEE,2013,33(12):72-80,188(in Chinese).
[3]朱国荣,王浩然,肖程元,等.抑制燃料电池单相逆变系统低频纹波的波形控制方法[J].中国电机工程学报,2014,34(18):2936-2943.
Zhu Guorong,Wang Haoran,Xiao Chengyuan,et al. Waveform control method for mitigation the low-frequency current ripple in the fuel cell single phase inverter system [J].Proceedings of the CSEE,2014,34(18):2936-2943(in Chinese).
[4]陈轶涵,韦徵,龚春英.平均电流控制型移相全桥DC-DC变换器输出阻抗及控制环路优化设计[J].电工技术学报, 2013,28(4):43-49.
Chen Yihan,Wei Zheng,Gong Chunying.Study of output impedance and control loop optimization for average current mode control phase-shift full bridge DC-DC Converter [J].Transactions of China Electrotechnical Society,2013, 28(4):43-49(in Chinese).
[5]彭良平,石峰,杜毅,等.双级式光伏并网逆变器母线电压二次纹波抑制[J].电力电子技术,2013,47(9):29-31.
Peng Liangping,Shi Feng,Du Yi,et al.A suppression method about the bus voltage of the secondary ripple of the double-stage photovoltaic grid-connected inverter[J]. Power Electronics,2013,47(9):29-31(in Chinese).
[6]周建.2 kW单相电力逆变电源系统的数字控制技术研究[D].南京:南京航空航天大学,2012.
Zhou Jian.Research on digital control technology for 2kW single-phase power inverter system[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2012(in Chinese).
[7]孙良伟.单相光伏并网发电系统中DC/DC变换器的设计与优化[D].杭州:浙江大学,2007.
Sun Liangwei.The design and optimization of DC/DC converters in single phase grid-connected photovoltaic system [D].Hangzhou:Zhejiang University,2007(in Chinese).
[8]王翀.两级式光伏并网逆变器及其功率解耦研究[D].南京:南京航空航天大学,2010.
Wang Chong.Research on two-stage PV grid-connected inverter and power decoupling[D].Nanjing:Nanjing Unive-rsity of Aeronautics and Astronautics,2010(in Chinese).
[9]Chen Y M,Liao C Y.Three-port flyback-type single-phase micro-inverter with active power decoupling circuit[C]. 2011 IEEE Energy Conversion Congress and Exposition, IEEE,2011:501-506.
[10]Kwon J M,Kwon B H,Nam K H.High-efficiency module-integrated photovoltaic power conditioning system[J].IET Power Electronics,2009,2(4):410-420.
[11]袁义生,张育源,陈进,等.两级式逆变器中间母线电压低频纹波抑制[J].电源学报,2016,14(3):38-46.
Yuan Yisheng,Zhang Yuyuan,Chen Jin,et al.Low frequency ripple rejection of the middle bus voltage of two stage inverter[J].Journal of Power Supply,2016,14(3):38-46(in Chinese).
[12]袁义生,张育源,周盼,等.抑制两级式逆变器中间母线电压二次纹波的方法[J].华东交通大学学报,2015,32(6):93-99.
Yuan Yisheng,Zhang Yuyuan,Zhou Pan,et al.A technique for the secondary ripple reduction of the bus voltage in two-stage DC-AC inverter[J].Journal of East China Jiaotong University,2015,32(6):93-99(in Chinese).
[13]张敬南,张军伟.基于数字控制的双向直流变换装置的设计[J].电力电子技术,2012,46(11):90-92.
Zhang Jingnan,Zhang Junwei.Bi-directional DC/DC converter unit based on digital control[J].Power Electronics,2012,46(11):90-92(in Chinese).
