基于遗传算法的起落架缓冲器变截面油针优化设计研究

吴志光，陈杰平，张陈荣

(1.池州职业技术学院 机电技术系，池州 247000) (2.安徽科技学院 机械工程学院，蚌埠 233100)

0 引 言

起落架作为飞机在着陆时吸收撞击能量的重要组成部分，其吸能和耗能能力的强弱对保证飞机安全性、舒适性至关重要。

为了提高起落架的吸能和耗能能力，即提高起落架的着陆性能，众多学者做出了突出的贡献。陈旺[1]中仅选主油孔直径，在其取值范围里取3个值，分别计算其对应的缓冲器功量曲线，对比功量曲线的饱满程度及缓冲器最大载荷的变化。洪学玲[2]选取最为敏感的参数，以缓冲器载荷绝对值最小为目标，获得最优设计。晋萍[3]对设计变量进行敏感度分析，以缓冲器载荷最大绝对值最小为目标，采用工程软件进行自动优化设计。李霞[4]以现有某型飞机起落架为基础，对其油针进行修形，提高了起落架着陆性能。吉国明等[5]假设缓冲器量油针为圆形截面且截面直径随油针轴向位置线性变化的规律，以缓冲效率为目标函数对起落架着陆性能进行优化设计。王明义等[6]建立摇臂式起落架的结构模型及数学模型，计算确定了缓冲器系统的各性能参数，采用能量法对这些参数进行了核验计算。李晓霏等[7]建立了起落架动力学模型和缓冲器模型，采用NSGA-Ⅱ算法进行了优化设计，得到了油针截面形状的最佳解，在降低轴向载荷的同时，增加了缓冲器效率。姜志良[8]建立变油孔缓冲器油针形状的优化模型，对油针横截面积进行优化及对油针分段位置和横截面积同时进行优化设计。以上均从不同角度对起落架缓冲器进行了优化设计研究，但未对起落架油针进行全面设计，所建立的优化流程缺乏飞机滑跑等综合情况分析。

NSGA-Ⅱ遗传算法是Kalyanmoy Deb提出的一种多目标优化遗传算法[9]，许多学者对此算法进行了大量研究和应用[10-12]。

本文以摇臂式起落架为例，首先利用平面多体动力学建立其数学模型，以文献[5]中的方法对起落架缓冲器进行初始设计，完成起落架的初始化；然后利用本文建立的起落架数学模型和NSGA-Ⅱ遗传算，以油针轴向不同位置的截面直径为设计变量，以起落架过载系数和缓冲效率为目标函数，对起落架缓冲器变截面油针进行优化设计，以提高起落架着陆性能。

1 起落架建模及NSGA-Ⅱ遗传算法

1.1 起落架建模

本文建立摇臂式起落架的数学模型，包括三个质量块和两个力单元。摇臂式起落架的受力分析如图1所示。

图1 起落架各部分受力分析图Fig.1 Force analysis diagram of parts of landing gear

①上质量块：将机身等效质量、起落架支柱及起落架支柱上的附属部件作为上质量块，上质量块承受升力、自身重力、缓冲器作用力以及惯性力，此外还承受摇臂的作用力。

②下质量块：将机轮组件作为下质量块，下质量块承受摇臂对机轮的作用力、自身重力、地面作用力以及惯性力。其中地面对下质量块的作用力的垂直分量与轮胎对地面的作用力为作用力和反作用力。

③中间质量块：将摇臂作为中间质量块，中间质量块承受支柱对其的作用力、缓冲器作用力、机轮对其作用力、自身重力以及惯性力。

④两个力单元：将缓冲器作用力和轮胎作用力分离作为两个独立的力单元。

各质量块既具有运动学属性也包括动力学属性。其动力学属性和运动学属性，以及各力单元为了便于求数值解，均采用的矩阵表述。动力学属性如表1所示，运动学属性如表2所示。

表1 摇臂式起落架数学模型的动力学表述Table 1 Dynamic expression of the mathematical model of articulated landing gear

表2 摇臂式起落架数学模型的运动学表述Table 2 Kinematical expression of the mathematical model of articulated landing gear

(1)

由上式判断中间质量块是否转动。

1.2 缓冲器力单元

缓冲器为单作动、被动式、油气式缓冲器，由内外筒组成。上腔为气腔，预填充压力为29.5 bar的空气或氮气；下部为油腔，填充介质为Skydrol 500 B磷酸酯液压油。缓冲器内筒外径为D1，对应面积为A1；内筒内径为D2，对应面积为A2；油孔直径为Do，对应面积为Ao；油针直径为Dp，如图2所示。

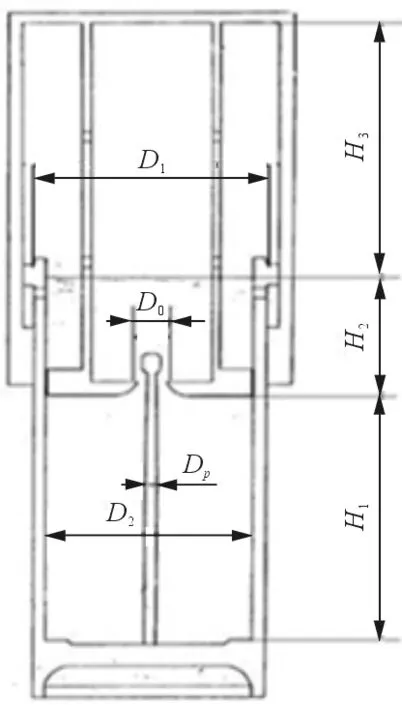
图2 缓冲器内部结构图Fig.2 Internal structure of buffer

规定缓冲器内外筒压缩时运动为正，伸张时运动为负。缓冲器内部受力如图3所示。缓冲器对外输出力Fs[13]为

Fs=Fh+Fa+Ff

(2)

式中：Fh为液体阻尼力；Fa为空气弹簧力；Ff为结构摩擦力。

图3 缓冲器内部受力分析Fig.3 Internal force analysis of buffer

液体阻尼力、空气弹簧力和结构摩擦力满足

(3)

式中[5]：ρ为缓冲器液压油密度；Cd为缓冲器流量系数，取值为0.7～1；s、s′分别为缓冲器行程和内外筒间的相对速度；An=A0-Ap为有效节流面积；Ah=A2-Ap有效压油面积；γ为气体多变指数；Aa=A1为气体作用面积；μ1为安装在内筒的上部轴承摩擦系数；F1为安装在内筒的上部轴承垂直作用力；μ2为安装在外筒的下部轴承摩擦系数；F2为安装在外筒的下部轴承的垂直作用力；s′/|s′|力的方向符号[13-14]。

流量系数Cd满足[15]：

Cd=0.8β2-0.481 3β+0.844 8

式中：β为油孔直径与来流腔直径的比值。

缓冲器外筒连接上质量块的点A，内筒连接中间质量块的点B。缓冲器内、外筒的相对运动可转化为点A和点B的相对运动。由平面多体运动学基本理论有：

(4)

(5)

缓冲器行程s及内外筒相对速度s′满足：

(6)

式中：l0为缓冲器外筒与支柱实际连接点到其投影点A的距离。

缓冲器力单元与其在全局坐标系的x向和y向的分量Fs,x、Fx,y满足：

Fx=(Fs,x,-Fs,y)T

(7)

1.3 轮胎力单元

机轮触地后轮胎发生弹性变形，并具有一定阻尼，将轮胎的力学模型等效为弹簧——阻尼模型。因此，轮胎单元力Ft满足：

(8)

式中：k为轮胎的弹性系数；c为轮胎的阻尼系数；y3为机轮质心O3在全局坐标系下的y向位置；R为机轮半径。

1.4 起落架求解流程

上文完成了起落架三个质量块和两个力单元的定义，以此建立摇臂式起落架着陆性能仿真模型，如图4所示。该模型的运行机理如下：

①各模型初始化，包括运动参数、结构参数等初始化。

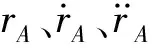
⑦缓冲器力单元，利用点A和点B的运动学参数计算缓冲器的行程、内外筒的相对速度，继而计算缓冲器作用力Fs并输出给上质量块动力学模型和中间质量块的动力学模型。

⑨是否满足中止指令？是，则终止计算；否，回到②继续计算。

图4 摇臂式起落架着陆性能仿真模型Fig.4 Simulation model of landing performance of articulated landing gear

1.5 NSGA-Ⅱ遗传算法

NSGA-Ⅱ遗传算法的运行机理如下：

随机初始化具有N个个体的父种群P0，对该种群进行非支配性进行排序，于是得到与其非支配程度相等的个体适应度值。在该适应度值的基础上进行二元锦标赛选择、交叉和变异操作，于是产生下一代子种群Q0。从第一代以后，循环执行过程如图5所示。

图5 NSGA-Ⅱ第二代以后的算法流程Fig.5 Algorithmic flow after second generation of NSGA-Ⅱ

对图5中的算法流程解释如下：

首先，将种群合并为一个具有2N个个体的种群Rt；然后，对种群Rt进行快速非支配性排序，形成前沿集合F=(F1,F2,…)；接着从第一个前沿起，顺序计算Rt中各非支配前沿中每一个体的密度信息(排挤距离)并将其并入新一代父种群Pt+1，循环执行该过程直到|Pt+1|+|Fi|≥N，此时利用比较运算符对Fi进行降序排序(因为根据拥挤距离排序，拥挤距离大的为优，所以需进行降序排序)，选择排好序的Fi中的前(N-|Pt+1|)个个体并入Pi+1中，至此完成了对新一代父种群的创建过程；最后，对新产生的父种群Pt+1进行二元锦标赛选择、交叉、变异操作，形成具有N个个体的新的子代种群Qt+1，当前代计算结束。

NSGA-Ⅱ算法为用户使用预留函数test_problem(double *xreal, double *xbin, int **gene, double *obj, double *constr)。用户利用该函数创建目标函数。

2 起落架着陆性能双目标优化设计

2.1 目标函数定义

本文进行起落架着陆性能优化设计的双目标函数为起落架过载系数和缓冲效率，分别定义如下：

①起落架过载系数 飞机着陆过程中作用在轮胎上的最大载荷与停机时轮胎上作用的载荷比，即

Ng=Ft,max/Ft,ave

(9)

②起落架缓冲效率 对于油气式缓冲器，通过落震试验获得其载荷——行程曲线，曲线下端所包络的面积与最大载荷最大行程组成的矩形面积比，即

(10)

式(10)中缓冲器在第一次压缩行程中对缓冲器做的功Ws满足：

Ws=∑Fs,iΔsi

(11)

式中：Fs,i为缓冲器在第i个时间间隔中受的载荷；Δsi为缓冲器在第i个时间间隔中的内外筒的相对位移，Δsi=si-si-1，si为缓冲器在第i个时间间隔末时缓冲器的行程。

2.2 设计变量定义

以缓冲器行程为0时，油针截面与其轴线的交点为原点并沿其轴线向油针根部方向建立油针轴向坐标，如图6所示。以10 mm为单位，沿油针轴向坐标建立节点x0=0，x1=0.01，…，x21=0.21，节点xi处对应的油针直径Dp,i的取值范围为20.0～25.0 mm。对于节点xi和节点xi+1间的油针直径采用线性插值获得，按式(12)确定。

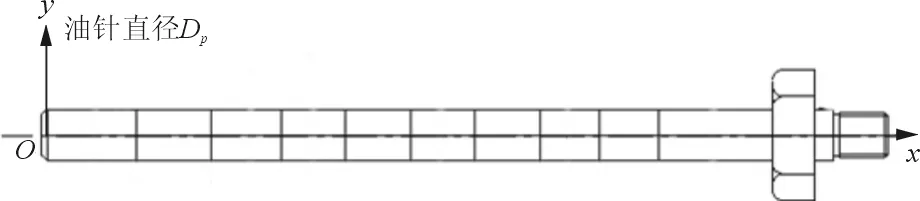
图6 油针示意图Fig.6 Diagrammatic sketch of oil needle

(12)

2.3 优化设计

min {Ng,1-η}

s.t. {0.020≤Dp,i≤0.025} (i=0,1,…,20)

(5)

在NSGA-Ⅱ遗传算法中为用户预留了函数test_problem(double *xreal, double *xbin, int **gene, double *obj, double *constr)定义目标函数。用于油针截面变化率设计的目标函数算法流程如下，即构造函数test_problem()：

①指针*xreal记录油针截面直径变化情况，其中*real[i]为油针轴向坐标xi(xi=i/100)对应的截面直径Dp,i。将数组(xi,Dp,i)写入文件pin.txt。

②运行起落架着陆性能仿真模型的程序LandingGearDesign()，按照图3模式进行计算，步长0.001 s，计算结束时间2 s。根据式(11)计算缓冲器实际做功，收集最大缓冲器作用力和最大行程；收集作用在轮胎载荷的最大载荷。

③根据式(9)计算起落架过载系数Ng、根据式(10)计算起落架缓冲效率η，并将Ng、1-η依次赋予目标函数Obj[0]和Obj[1]。

完成函数test_problem()定义后，运行NSGA-Ⅱ主程序，种群规模为100，进化代数为200，交叉概率为0.9，变异概率为0.125。

2.4 结果分析

用于进行起落架着陆性能优化设计的缓冲器内部结构参数值如表3所示。

表3 缓冲器初始参数Table 3 Initial parameters of buffer

优化前，根据图4所示的摇臂式起落架着陆性能仿真模型自编程序，计算采用直径为22.2 mm的定截面油针，其过载系数Ng=1.343，缓冲效率η=70.15%，缓冲器最大行程为202 mm。

采用本文提出的方法进行起落架着陆性能双目标优化设计，计算结果如表4所示，优化后的起落架过载系数减小到1.151 5，起落架缓冲效率η提升到84.94%，缓冲器行程s约为194 mm。优化后的缓冲器油针模型如图7所示。

表4 基于NSGA-Ⅱ和起落架着陆性能仿真 模型设计的变截面油针参数Table 4 Variable cross section oil needle parameters based on NSGA-Ⅱ and landing performance simulation model design

图7 优化后的缓冲器油针模型Fig.7 Optimized oil pin model of buffer

2.5 优化结果验证

利用基于LMS Virtual.Lab Motion和LMS Imagine.Lab AMEsim的联合仿真技术的虚拟落震方法[5]，对优化前后的起落架着陆性能进行验证，如图8所示。

(a1) 缓冲器载荷行程曲线

(a2) 轮胎载荷-时间曲线 (a) 优化前

(b1) 缓冲器载荷行程曲线

(b2) 轮胎载荷-时间曲线 (b) 优化后图8 起落架着陆性能优化前后缓冲器功量 曲线及轮胎载荷对比Fig.8 Comparison of buffer power curve and tire load before and after landing performance optimization of landing gear

从图8可以看出：优化后缓冲器的载荷和行程较优化前有所减小，缓冲器功量曲线较饱满，表明缓冲效率有所提高；优化后轮胎的法向载荷较优化前明显减小，对应的过载系数减小。

3 结 论

(1) 优化后起落架缓冲效率提高，起落架过载系数降低；改善缓冲器性能的同时也改善了轮胎的载荷环境，综合提高了起落架着陆性能。

(2) 采用NSGA-Ⅱ多目标遗传算法经仿真技术验证可以有效地指导油针形状设计，可以作为起落架缓冲器试验的指导及改型的依据。但是对于建立的缓冲器模型还有待完善，采用有侧油孔及变油孔的模型能够提高模拟的真实性。

[1] 陈旺. 小车式起落架落震及全机着陆动态仿真分析[D]. 南京: 南京航空航天大学, 2005.

Chen Wang. Research on dynamic simulation for dropping of truck-like landing gear and landing of aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2005.(in Chinese)

[2] 洪学玲. 基于ADAMS的小车式起落架着陆及全机滑跑动态仿真[D]. 南京: 南京航空航天大学, 2008.

Hong Xueling. Dynamic simulation for landing of truck-like landing gear and taxing of aircraft based on ADAMS[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008.(in Chinese)

[3] 晋萍. 飞机起落架动态性能仿真分析[D]. 南京: 南京航空航天大学, 2003.

Jin Ping. Simulation analysis of dynamic behavior for airplane landing gear[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2003.(in Chinese)

[4] 李霞. 现代飞机起落架缓冲性能分析、优化设计一体化技术[D]. 西安: 西北工业大学, 2004.

Li Xia. Integration of shock performance analysis, design of aircraft landing gears[D]. Xi’an: Northwestern Polytechnical University, 2004.(in Chinese)

[5] 吉国明, 董萌, 张量. 摇臂式起落架初始设计方法研究及性能仿真[J]. 科学技术与工程, 2011, 11(22): 5345-5349.

Ji Guoming, Dong Meng, Zhang Liang. Study of early design method and co-simulation of the performance on articulated landing gear[J]. Science Technology and Engineering, 2011, 11(22): 5345-5349.(in Chinese)

[6] 王明义, 贾玉红. 基于能量法的缓冲器参数设计[J]. 振动与冲击, 2005, 24(6): 117-119.

Wang Mingyi, Jia Yuhong. Parameter design of buffer based on energy method[J]. Journal of Vibration and Shock, 2005, 24(6): 117-119.(in Chinese)

[7] 李晓霏, 许锋. 起落架虚拟试验及性能优化[J]. 江苏航空, 2016(4): 12-15.

Li Xiaofei, Xu Feng. Virtual test and performance optimization of landing gear[J]. Jiangsu Aviation, 2016(4): 12-15.(in Chinese)

[8] 姜良志. 大型客机起落架缓冲系统优化设计技术研究[D]. 南京: 南京航空航天大学, 2010.

Jiang Liangzhi. Study on optimization design technology for landing gear shock-absorbing system of large civil aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010.(in Chinese)

[9] Kalyanmoy Deb, Samir Agrewal, Amrit Pratap, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-Ⅱ[C]. Proceeds of the Parallel Problem Solving from Nature VI Conference, 2000: 304-311.

[10] 李玥. 基于多目标遗传算法的航空发动机多目标优化控制[D]. 南京: 南京航空航天大学, 2007.

Li Yue. Multi-objective optimization of aeroengine control based on multi-objective genetiv algorithms[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007.(in Chinese)

[11] 张萍. 多目标优化遗传算法在建筑协同设计冲突消解中的应用[D]. 济南: 山东师范大学, 2009.

Zhang Ping. Application of MOGA in conflict resolution for architecture cooperative design[D]. Ji’nan: Shandong Normal University, 2009.(in Chinese)

[12] 王广博, 韩庆, 钟小平. NSGA-Ⅱ中重复个体的控制[J]. 科学技术与工程, 2011, 11(34): 8602-8604.

Wang Guangbo, Han Qing, Zhong Xiaoping. The control of overlapping solutions in NSGA-Ⅱ algorithm[J]. Science Technology and Engineering, 2011, 11(34): 8602-8604.(in Chinese)

[13] Milwitzky B, Cook F E. Analysis of landing-gear behavior[R]. NACA Report 1154, 1953.

[14] 蔺越国, 程家林, 冯振宇, 等. 飞机起落架缓冲支柱参数化模型及优化分析[J]. 系统仿真学报, 2008, 20(10): 2732-2735.

Lin Yueguo, Cheng Jialin, Feng Zhenyu, et al. Parameter modeling and optimization analysis for landing gear absorber[J]. Journal of Simulation, 2008, 20(10): 2732-2735.(in Chinese)

[15] James N Daniels. A method for landing gear modeling and simulation with experimental validation[R]. NASA Constractor Report 201601, 1996.