移动机器人目标物体识别研究

许金波+杨晶东+韩太军

摘要：

基于视觉信息的运动目标识别是室内移动机器人自主导航的重要研究内容。背景噪声干扰、自然光照、机器人视角变化等因素经常影响识别稳定性。针对该问题，提出一种有效的目标物体识别方法，采用体素网格滤波和支持kd-tree结构对点云数据有效组织，以识别复杂环境中的物体。实验表明，该方法在满足实时性前提下，相比传统迭代最近点、采样一致性初始配准算法具有更高的准确率，更适合复杂环境下的物体识别。

关键词：

物体识别；点云滤波；迭代最近点；采样一致性初始配准算法

DOIDOI：10.11907/rjdk.172033

中图分类号：TP301

文献标识码：A文章编号文章编号：16727800（2018）001001405

Abstract：Moving object recognition based on visual information is an important research content of autonomous navigation of indoor mobile robot. The existing methods often affect the stability due to background noise interference， natural light and robot angle change. An effective target object recognition method is proposed for this problem， and the object in the complex environment is identified by using the voxel mesh filtering and supporting the kdtree structure to effectively organize the point cloud data. Experiments show that the method of sampling coherence initial registration algorithm has higher accuracy and more suitable for object recognition in complex environment than the traditional iterative nearest point under the premise of satisfying realtime.

Key Words：object recognition； point cloud filtering； iterative closest point； initial registration algorithm

0引言

利用視觉对物体进行识别，广泛应用于图像检索、机器人抓取、场景识别和移动定位。点云旋转错位、平移错位以及点云的不完整性等影响物体点云匹配识别的精准性。点云的配准指通过摄像头在不同角度下扫描获得点云数据，这些点云数据之间有一定的重叠区域，通过变换坐标，可以将多幅点云数据合并到同一直角坐标系下。

目前常用的点云匹配算法包括经典的迭代最近点（Iterative Closest Point，ICP）算法、基于欧式距离不变性的Greedy bound算法、采样一致性初始配准（Sample Consensus Initial Alignment，SACIA）算法和利用kd tree加速搜索算法、优化ICP算法，实验效果都较好，但存在庞大数量级点云匹配时的时间效率问题。面对大数量级别的点云集合（大于100 000个点）对应的刚体变换，Martin Magnusson提出了利用正态分布算法加以优化，这种思路在时间效率上有了很大改进，但在局部准度上却有所降低。本文提出一种基于点云特征的目标识别方法（IICP—SACIA），在获得点云原图后对其进行体素网格滤波，采用改进的ICP算法和SACIA算法匹配识别物体的点云特征，最大限度地滤除了背景点云，有效提高了算法的识别效率。实验表明该方法在室内环境下能有效识别物体特征，满足了移动机器人视觉自主导航要求。

1相关理论

1.1物体识别原理

物体点云匹配识别指通过摄像头在不同角度下扫描获取点云数据，这些点云数据之间有着一定的重叠区域。通过变换坐标，可以使多幅点云数据叠合到同一直角坐标系下，最终得到物体的点云准确配准。三维空间上的几何模型变换一般含有平移、缩放和旋转，本文研究的点云匹配是刚性点云匹配，在不考虑缩放的前提下，通过求得目标点云集Q到源点集P的平移向量W和旋转矩阵B，使坐标变换后得到的转换矩阵（B*P +W）与Q之间的距离最小，即求min‖Q-（B×P+W）‖＼+2。

1.2改进的迭代最近点算法

传统的迭代最近点（Interative Closest Point，ICP）是经典的点云匹配算法，运用四元素模型，经过最小二乘法迭代运算来最小化源点云和目标点之间的欧式距离函数，继而完成空间上自由曲面的配准问题。算法过程：①在两组点云中查找多对点，在这些点对里，其中的一个点在目标点云中，另一个在待配准点云里，两者之间满足欧式距离最近；假设某一点对之间的距离小于给定阈值，即能确认两个点云对之间存在一一对应关系；②构造所有成对点之间的“距离误差和”的目标函数，求取变换矩阵，要求目标函数值最小，也就是整体对点之间的距离之和最小；③迭代运算，重复上述过程，一直到距离误差和的值小于给定阈值或者运算达到最大迭代次数为止；④假如最后配准效果满足指标要求，即将通过整体变换后的待配准点云叠加到目标点云图中，完成该对点云的配准。endprint

本实验粗配准阶段使用改进的ICP算法：

（1）点云的准确性：Mitra等证明了点对的正确性对ICP结果的重要性，提出当输入点云自身存有较多噪声时，算法会把不正确的点对配对在一起，使匹配的过程不收敛。本实验对点云图像体素化网格滤波的预处理操作就是为了防止这种情况发生，为匹配过程奠定良好基础。

（2）捜索策略：ICP算法效率不高的一个重要原因是，每次迭代都需要遍历整个点云中的点用以搜素匹配的点对，本实验运用kdtree结构对点云数据进行合理组织，加快了ICP算法的搜索效率。

（3）去除错误点对：当经过ICP算法匹配完成后，不是所有的匹配关系都符合要求，错误配对的点对将对旋转矩阵和平移矩阵的运算产生负面干扰，这些有误差的配准点对应在精确配准阶段剔除。排除手段有阈值、比例、分布等。本实验运用较为简单的最大欧氏距离来限制约束，就是当匹配后的点对Yi和Xi的欧氏距离大于预设的限制Dmax时，判断为一个错误的匹配，不参与矩阵估计。假如产生一对多的情况，仅仅取与目标点云欧氏距离最近的那个点作为其对应点，剔除错误的对应关系。

1.3采样一致性算法配准原理

SACIA配准是根据点云的FPFH特征展开的，匹配原理与过程如下：

设目标点云为Q，待配准点云为P，①n个采样点选取自待配准点云P，这些采样点满足两两之间的距离大于dmin，即预先给定最小距离阈值，偏向于拥有不同的FPFH特征，这样在不影响点云整体特征统计的同时降低计算量；②针对点云P中的每个样点，在目标点云Q中查找与P中该点拥有类似FPFH特征的一系列点，也就是说P中的一个采样点也许会在Q中匹配到多个与之相似的点；③运算从P中选择的n个采样点与在Q中查找到的对应点刚体变换矩阵，依次求得所有对应点变换之后的“距离误差和”函数，判断当前配准变换效果。这时的距离误差和函数一般用Huber罚函数表达，

式（1）中：第i组对应点在变更之后的距离差是li，ml为给定值。目的是寻求一个最优的变换，把误差函数值降到最小，此时的变换即是最终的匹配变换矩阵所得的匹配结果。

2物体识别

2.1点云滤波

因为深度体感相机采集的原始點云数据庞大，直接用来配准会加大计算机系统运算负担，降低匹配效率。本实验运用点云体素化网格滤波，在物体识别之前对点云进行滤波，可使体感相机获取点云细节特征，具有较高的配准率。VG滤波器用以建立一个三维体素栅格，体素重心的点用下式表示：

式（2）中：Pl为体素基元，Pmin为点云最小点，Pmul为点云中体素基元Pl各个方向上的扩展体素，Pid为该点体素重心，Round为基于基元Pl的矢量积，取整函数。

针对480×640深度图像，采用体素网格法向下取整，得到体素范围内具有相同标识点云簇。计算点云在体素Pl下重心Pid信息。该方法对于曲面采样点具有较高效率，能有效降低点云密度，确保局部点云特征。体素滤波要考虑点云压缩效率和后期处理时间，确保在点云特征不丢失前提下设定压缩参数。

图1、图2分别是点云图和VG滤波后点云图（见封二彩图）。可以看出滤波后点云密集度降低。VG滤波器将源点云数据根据体素比例投影到新点云集合中，在新集中每一个点都有唯一ID标识，根据ID对源点云进行处理，经过VG滤波后，可滤除不必要的点云簇，有效提高后期物体识别效率。经过多次体素滤波可得到拥有最佳点云特征的体素值。

2.2计算点云的法线特征

在不干扰整体点云几何特征的情况下，降低点云几何特征的运算量，对点云数据集进行体素网格滤波等处理，获得点云几何特征流程如图3所示。

获得点云的局部几何特征直方图（Point Feature Histograms，PFH）。几何曲面中一个重要特征即是表面法线，广泛运用于计算机图形处理。一组点云数据集，运算全体点的法线方式有以下两种：①依据曲面网格化（surface mesh）技术，对所获得的点云数据进行曲面重建，然后依据重建的曲面计算其法线向量；②不进行曲面重建，而是用一组点云数据计算每一组点的法线。

本文运用第②种方法，曲面上的某一点法线以该点在曲面上的相切平面的法线所代替，因此到相切平面的拟合估计通常依据最小二乘法拟合。设需求点为p，其坐标为（x，y，z）＼+T，其k 个邻域点为Pi，则在待求点处构造协方差矩阵R如式（3）：

式（4）中：k为正整数，用来对特征值计数。协方差矩阵说明了待求点的局部变化。另外，该点处法线的走向依据协方差矩阵的最小特征值的特征向量来估算。

2.3物体识别

通过对原点云进行体素网格滤波处理，再依据物体特征直方图进行物体识别。

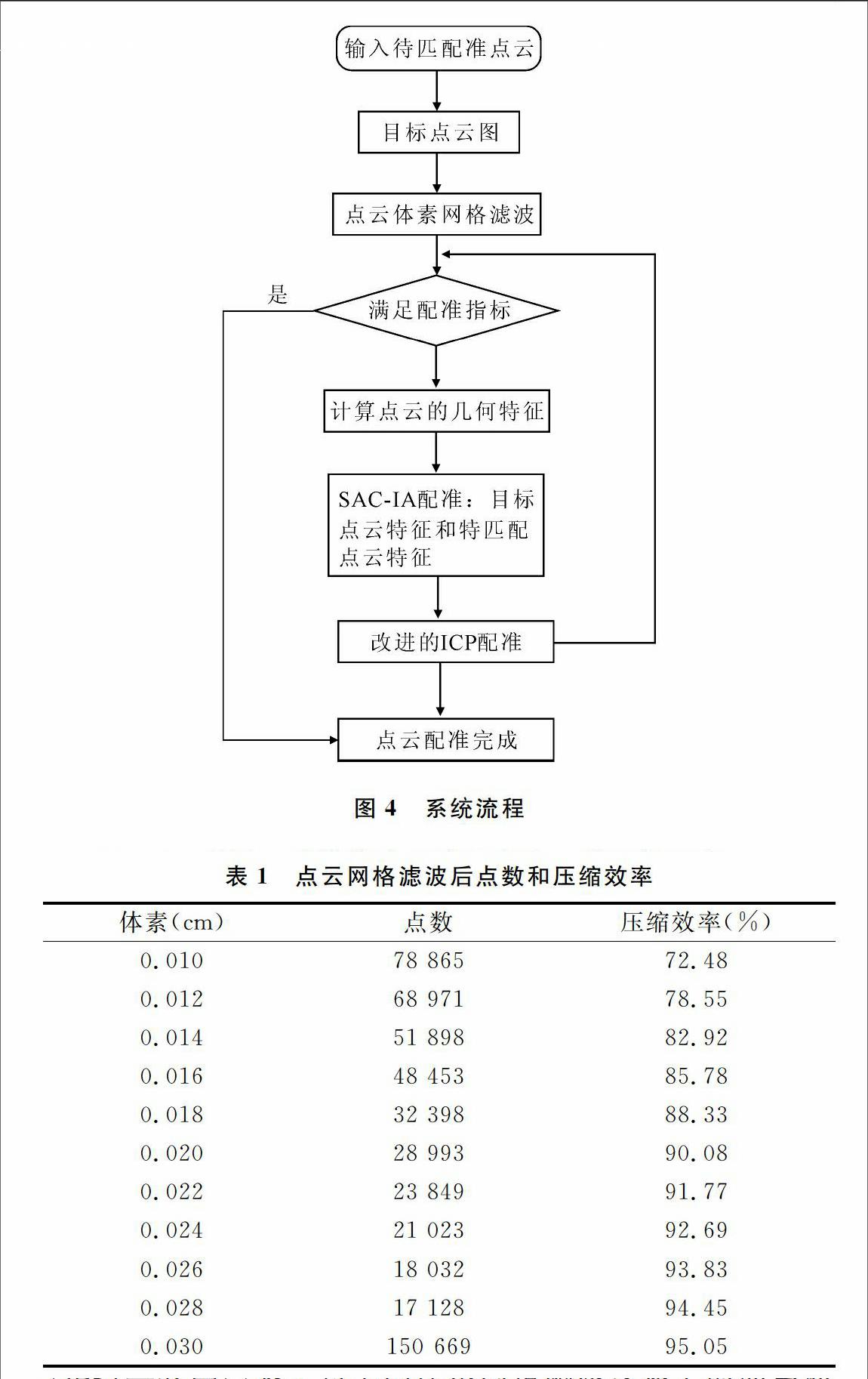
深度相机点云簇形状不规则且分布不均匀，可在3D空间使用固定宽度体素网格表示，并采用kd-tree结构填充。该结构具有二叉树结构，且不需空间等分，比八叉树更好地包围图元。运用采样一致性算法对待匹配点云进行粗配准，最后结合改进的ICP对点云进行细配准以提高配准准确度。系统流程如图4所示。

设Po为单位向量，l为体素长度。Pp、Pr为人、物体、机器人位置，算法描述如下：

Start输入源点云Pin

Step1设置基元体素Pl进行滤波

（1）体素参数Pl=Po/（l，l，l）

（2）获取点云最大Pmax，Pmin，计算在x、y、z方向点云体素矢量Pdiv=（Pmax-Pmin）*Pl

（3）体素矢量积Pmul=（1，Pdiv[0]，Pdiv[0]Pdiv[1]，0）

（4）计算所有乘积系数点云簇Pid见公式（2）

（5）如果Pid只有一个，则P=Pin；若有n个Pid相同，则P=（∑Pin）/n，遍历所有点endprint

Step2根据相机高度Hc，计算直通滤波参数

Step3对VG滤波后的点云Pi填充kdtree结构

Step4采用一致性算法對待匹配点云进行粗配准

Step5采用IICP算法精准匹配，输出结果

End

3实验分析

在室内进行物体识别实验，其中部分实验是在灯光照明环境下进行。操作系统为Ubuntu 12.04，CPU 为Intel（R） Core（TM） i3 2.53GHz，内存为2GB。

3.1体素网格滤波

图5、图6分别是点云图和体素网格滤波后点云图（见封二彩图），表1为不同体素网格滤波参数下的点云簇和压缩效率变化。

由表1可以看出，随着点云体素增加，滤波后点数逐渐减少，压缩效率接近饱和。此时，点云簇中的每个点云特征具有最基本的单体特性，点云体素网格滤波对物体识别过程影响较小。表2为不同体素下物体识别各阶段与平均时间偏差率。

表2中的正负数表示超出和低于平均时间，由此得出，滤波偏差率在-4.55%～7.15%之间波动，识别偏差

率处于-15.52%～9.48%之间。由表2可分析出，当体素值为0.01，且参数在0.02～0.023之间时，滤波偏差率波动较大，处理各阶段所需时间较长，不能稳定识别物体。当体素值大于0.027时，特征点云点数趋于饱和，滤波趋于稳定，不同体素参数下滤波点数也趋于一致。但如果体素参数无限增大，可能导致场景中各特征点云相互融合，丢失部分有效的特征点云。因此，在满足所需点云特征前提下，选择合理体素可有效提升点云识别效率。

3.2物体识别

在实验室环境下进行物体识别实验，按照简单环境识别和复杂环境识别，分析物体识别后的距离均方误差变化情况。图7、图8为物体在简单环境下的识别中体素网格滤波和最后的滤波效果（见封二彩图）。

针对以上场景可测得物体识别后的距离均方误差，图8为物体点云配准输出效果图，可以看出简单环境下物体的识别效果达到了预期要求。

图9、图10为复杂环境下的物体识别实验（见封二彩图），环境中待识别物体处于两个干扰物中间，图11、图12、图13为物体在复杂环境下运用IICP算法、SACIA算法、联合IICP和SACIA算法识别效果（见封二彩图）。

ICP和SACIA两种配准算法的配准效果并不客观，两幅物体点云中存在严重偏差。为了获得更精准的配准效果，本文提出了一种结合SACIA算法以及改进的ICP配准算法的点云配准进行改进。对点云进行一次SACIA匹配，作为粗配准准备，提升配对点云的吻合度；运用改进的ICP做一次精配准，得到最后的效果图。因为历经了一次初始的预配准，点云之间的差异大大降低，所以，运行改进的ICP配准能更快收敛，得到更好的配准性能，明显降低了迭代次数，节省了运行时间，提升了配准概率和配准效果。

为了比较配准效果，以“橄榄油包装盒”点云为配准模型，与上述效果进行对比。在改进的ICP算法及SACIA基础上，将SACIA的最大迭代次数由500降低为350，缩短了运行时间，最后由改进的ICP来进行精准配准。由表3看到，联合优化的配准总时间为268 009ms，其中SACIA配准用时304 588ms，改进的ICP配准用时51 133ms。利用联合优化的点云配准流程后，得到“橄榄油包装盒”模型的源点云和目标点云，如图13所示。从图13可以看到，两帧点云中物体盒子的各个部分都得到了良好的配准。完成联合配准后源点云和目标点云一一对应点对的距离误差平方值，如图14～图16所示。基于改进的ICP联合SACIA对应点对的距离均方误差结果约为：1.12e-6。

从表3可以得出，仅仅使用改进的ICP 算法运行时间最短，但距离均方值误差最大，配准结果最不理想；单单使用SACIA 算法的运行时间最长，距离均方差较小，但部分区域偏差较大；SACIA算法和改进的ICP算法组合配准方式的运行时间比SACIA 的时间少，且匹配后的距离均方误差很小，此组合优化匹配效果最好。

4结语

本文提出了一种有效物体识别算法，对基于深度视觉的原点云进行体素网格过滤，通过改进ICP算法和优化配准流程实时对物体进行识别。实验表明，该算法相比单纯IICP算法和SACIA算法具有更高的准确率，相比于ICP算法具有更高的识别速度。在确保实时性前提下，较其它物体识别方法具有较高的识别精度和稳定性，提高了自主机器人目标跟踪的鲁棒性。

参考文献：

[1]马尔，姚国正，刘磊，等.视觉计算理论[M].北京：科学出版社，1988.

[2]ZHANG Z.A flexible new technique for camera calibration[J]. Pattern Analysis and Machine Intelligence， IEEE Transactions， 2000，22（11）：13301334.

[3]陈阳.三维点云数据配准方法研究[D].天津：天津大学，2014.

[4]WILMA PAIRO1， JAVIER RUIZDELSOLAR， RODRIGO VERSCHAE1， et al.Person following by mobile robots： analysis of visualand range tracking methods and technologies[C]. 17th annual RoboCup International Symposium， 2014.

[5]HONG HAN， JINGXIANG GOU.Sparse geometric features for visual detection and estimation.image feature detection and description[J].Neurocomputing， 2013，120（1）：192202.endprint

[6]RUSU R B， BLODOW N， BEETZ M. Fast point feature histograms （FPFH） for 3D registration[C]. Robotics and Automation， IEEE International Conference， 2009：32123217.

[7]FELZENSZWALB PF， GIRSHICK R B， MCALLESTER D， et al. Object detection withdiscriminatively trained part based models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2010，32（9）：120.

[8]BENTLEY J L. Multidimensional binary search trees used for associative searching[J]. Communications of the ACM， 1975，18（9）：509517.

[9]RUSU R B， COUSINS S. 3D is here： point cloud library （pcl）[C]. Robotics and Automation （ICRA）， IEEE International Conference， 2011：14.

[10]戴靜兰，陈志杨，叶修梓.ICP算法在点云配准中的应用[J].中国图象图形学报，2007，12（3）：517521.

[11]EMI MATSUMOTO， MICHLE SEBAG，EINOSHIN SUZUKI.Using SVM to avoid humans： a case of a small autonomous mobile robot in an office[C]. Computer and information Sciences， 2011.

[12]王欣，张明明，于晓，等.应用改进迭代最近点方法的点云数据配准[J].光学精密工程，2012，20（9）：20682077.

[13]解则晓，徐尚.三维点云数据拼接中ICP及其改进算法综述[J].中国海洋大学学报：自然科学版，2010（1）：99103.

[14]杨现辉，王惠南.ICP算法在3D点云配准中的应用研究[J].计算机仿真，2010（8）：235238.

[15]ROBIN STRANDA， BENEDEK NAGYB， GUNILLA BORGEFORSC. Digital distance functions on threedimensional grids[J].Theoretical Computer Science， 2011，412（15）：13501363.

[16]STEPHEN J REDMOND， CONOR HENEGHAN. A method for initialising the Kmeans clustering algorithm using kdtrees pattern[J]. Recognition Letters， 2007，28（8）：965973.

[17]刘博源，陆明刚，阚文涛.激光扫描表面特征的点云数据处理方法[J].光学仪器，2016，38（1）：4144.

[18]钱炜，付东翔，李晓燕，等.越障机器人的设计与研究[J].上海理工大学学报，2002（3）：264267.

（责任编辑：杜能钢）endprint