考虑“井工厂”学习效应的平台位置优化方法

王志月 高德利 刁斌斌 胡德高

1.中国石油大学石油工程教育部重点实验室 2.中石化重庆涪陵页岩气勘探开发有限公司

页岩气开发过程中，在丛式水平井井网部署方式确定以后，所面临的关键问题之一就是平台位置优选，主要包括确定平台的位置和数量，确定每个平台与靶点的对应关系。由于丛式水平井投资巨大，对平台位置进行优选能够有效降低钻井费用。Devine和Lesso[1]最早针对海上平台位置优选问题进行了研究。此后，诸多学者对此问题进行了探讨，所建立优化模型的目标函数主要包括总井深最小、水平位移之和最小[2-4]及钻井费用最少[5-10]，模型求解算法主要包括隐式枚举法[5,7]、图论算法[2,10]、聚类分析法[3]及遗传算法[4]等。上述研究中，通常将常规定向井和水平井作为研究对象，在以钻井费用作为优化目标时，目标函数通常是单井钻井费用的累加。然而，随着“井工厂”技术的不断发展[11-12]和应用[13-15]，“井工厂”模式所产生的学习效应对钻井费用起到重要影响，也是影响平台位置优选的一个重要因素。

1 “井工厂”钻井学习指数

“井工厂”模式下，若所钻井的井型相似，则随着钻井数量的增加，平均单井钻井费用会出现降低的趋势。其原因主要是由于对同一平台上多口井进行流水线作业即依次一开、固井，二开、再依次固完井[16]，通过新型钻井液重复利用降低钻井液用量[17-18]。并且随着钻井数量的增加，作业者会更加熟悉地层情况，获得更多的钻井经验从而提高钻井效率。这种现象可以用学习曲线来表征，Ikoku[19]首先提出了钻井学习曲线的方程：

式中n表示钻井次序；gn表示第n口井的钻井费用。a、b表示针对某一区块通过非线性回归估算的参数。

图1给出了单井钻井费用随着钻井次序的变化趋势。

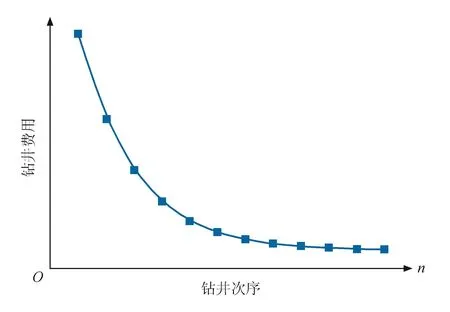
图1 单井钻井费用与钻井次序关系的示意图

Brett和Millheim[20]改进了Ikoku的学习曲线表达式，并给出了一个更符合实际的方程为：

式中C1表示钻最后1口井与钻第1口井相比所节约的费用；C2表示表征学习效率的一个常数；C3表示学习曲线的渐近线，表示钻井极限费用。

为更好地评价“井工厂”模式下学习效应对丛式井平均单井钻井费用的影响，笔者提出了钻井学习指数的概念，在钻井学习曲线已知的前提下，定义每个平台钻n口井的平均单井钻井费用与该平台上钻第一口井的钻井费用的比值为钻井学习指数，根据式（2）可得钻井学习指数的表达式为：

式中I(n)表示钻n口井的钻井学习指数。

2 “井工厂”模式下平台位置优化模型

丛式水平井平台位置优化问题可表述为：在给定水平井水平段位置的前提下，优选平台位置、数量以及平台与水平段的分配使总的钻井费用最小。显然这属于0-1整数规划问题，首先需要对目标函数和约束条件进行阐述，然后建立最优化模型。

在页岩气开发总费用中，钻井费用及压裂费用所占比例极大，但由于压裂费用不受平台与水平段间相对位置的影响，因此在进行平台位置优化时不考虑在内。单井钻井费用与井眼轨道、套管设计、钻完井技术等密切相关，在钻完井施工方案确定的前提下，单井钻井费用可看作关于水平段长度、井口与水平段首靶点间横向位移和纵向位移的函数。图2表示平台位置与水平段之间的相对位置关系，O点代表平台，AB代表水平段。

图2 平台位置与水平段之间的相对位置示意图

参照本文参考文献[8]，本文所采用的第j个平台完成的第i口井的单井钻井费用的函数表达为fi,j（li,σi,j, ηi,j），即

其中

式中li、σi,j和ηi,j分别表示第i个水平段的长度、第i个水平段与第j个平台之间的纵向偏距和横向偏距；d1、d2、d3、d4、d5表示单井钻井费用的相关系数；Xj、Yj表示第 j个平台的中心点坐标 ；xA,i、yA,i、xB,i、yB,i分别表示第i个水平段跟端和指端的坐标。

若考虑平台建设费用，则平台建设费用可看作关于平台钻井数量的函数，其表达式为：

式中Pj表示第j个平台的建设费用；μ表示单位面积平台的建设费用；Nj表示第j个平台的钻井数量；a0、b0为常数。

约束条件主要包括每个平台所允许的最大钻井数量，单井最大钻井费用以及单井的轨道复杂度等，其中，轨道复杂度的约束体现在钻井费用的函数表达式里。综上所述，可得到考虑“井工厂”学习效应的平台位置优化模型。

目标函数：

约束条件：

且

其中，Z表示总的钻井费用；I(Nj)表示第j个平台钻Nj口井的钻井学习指数；Np表示待建平台数量；Nw表示待钻井数量；Pj表示第j个平台的建造费用。ti,j为决策变量，若第i口井由第j个平台完成，ti,j=1，否则ti,j=0。式（9）表示每口井只能分配给一个平台，式（10）表示每个平台的钻井数量不能超过其最大容量。式（11）表示单井钻井费用不能超过所允许的最大钻井费用。式（10）和式（11）同时可以保证同一个平台所钻井的井型相似，以更好地应用“井工厂”技术。

3 求解方法

针对所建立的优化模型，本文采用遗传算法进行求解。遗传算法是模拟自然界生物进化过程的随机搜索算法，依照优胜劣汰的原则，通过基因编码、选择、交叉、变异等操作使得子代个体较父代个体能够更好地适应给定的适应度函数，从而得到问题的最优解或近似最优解[21]。

3.1 初始化与编码

初始种群通过随机选择产生，在编码过程中采用二进制编码，如果待钻井数和平台数分别为Nw和Np，则决策矩阵为Nw×Np。决策矩阵中，每行有且只有一个1，表示每口井只能由一个平台完成钻井，各列之和不能大于Nmax，表示平台的钻井数量不能超过其最大容量。为方便运算，将决策矩阵转换成含有Nw×Np个元素的向量，并代表一个染色体。以3个平台3口井为例，编码过程如下：

3.2 选择

在选择操作中，依据给定的适应度函数选择适应度函数值最高的染色体进行下一步的操作。为保证第j个平台的钻井数量Nj不大于平台最大容量，运用罚函数法对适应度函数进行限定，如果平台的钻井数量大于平台最大容量，则加入惩罚项对其进行惩罚。适应度函数表达式如下式所示。

当时：

式中F表示适应度函数；fmax表示单井钻井费用所允许的最大值；Cmax表示平台建造费用的最大值；σ表示惩罚因子。

通常情况下，水平井需要有一定的靶前位移以避免较大的鱼钩型井出现从而降低钻井复杂度，为此，在进行平台位置选择时，限定平台中心点到水平段垂线的垂足不能位于水平段内，否则，在钻井费用函数中加入惩罚项。平台中心点到水平段垂线的垂足坐标可由下式计算得出：

若垂足位于水平段内，那么垂足坐标将满足：

相对应的单井钻井费用函数由式（18）表示：

式中ω表示惩罚因子。

在选择操作中，计算出每个染色体的适应度函数后，采用轮盘赌方法进行选择，染色体的选择概率可由下式计算得出。

式中pi表示第i个染色体的选择概率；β表示表征选择概率的常数；Fi表示第i个染色体的适应度函数值；Fmax表示种群中适应度函数的最大值。

3.3 交叉

交叉操作可以随机交换两个染色体的基因并生成新的染色体，本文采用单点交叉的方法，考虑到所建立模型中的约束条件，采用式（20）进行交叉位置的计算，并交换交叉位置之后的基因。

式中Pcross表示交叉位置；unidrnd（Nw－1）表示随机产生一个1到Nw－1之间的整数。

3.4 变异

变异操作能够随机改变所选的染色体基因，由此避免算法陷入局部收敛。

以3口井、3个平台为例，交叉和变异操作的示意图如图3所示。

4 算例分析

根据待选平台位置的分布特点进行两个算例的计算。在算例中，假定丛式水平井的垂深相同，水平段长度均为1 500 m，水平段横向间距为400 m，水平段由靶点A和靶点B确定且两个靶点的钻井顺序不固定，第i口井由第j个平台完成时的单井钻井费用的函数表达式及钻Nj口井的平台建设费用的函数表达式分别为：

图3 遗传算法的交叉和变异操作图

在钻井学习指数表达式中，C1、C2、C3分别取80、0.12、80。

在遗传算法参数中，交叉概率和变异概率分别取0.8和0.2；算例1中种群规模为300，算例2中为500；迭代次数均为200次。

4.1 算例1

已知某区块计划布井数为16口，经测量后确定了15个待选平台位置，每个平台所能容纳的最大钻井数为16。水平段靶点坐标及待选平台坐标分别如表1、2所示。

优化计算结果如表3、4所示。图4中绿色正方形代表待选平台位置，直线段代表水平段。图4-a为考虑学习效应的平台优化结果，图4-b为不考虑学习效应的平台优化结果。从图4中可以看出，相对于不考虑学习效应的优化结果，考虑学习效应后可以将平台数由4个降到2个，每个平台的钻井数量由4口井变成8口井；考虑学习效应的建井井总费用为1 345.4万美元，相对于不考虑学习效应的建井总费用1 769.8万美元，总费用减少24%。此外，平台个数的减少也将会减少管线集输费用及后期管理费用从而产生更大的经济效益。

4.2 算例2

若只给定待选平台位置的可行区域，那么首先需要对该区域进行网格划分，每个网格可看作100 m×100 m的区域并代表1个平台的位置。在此算例中，靶点数据如表4所示，待选平台坐标范围假定为X∈（－200，200），Y∈（－300，400），由此可得待选平台数为40。为避免大鱼钩井的出现，通过约束方程（18）确保被选平台和水平段之间存在一定的靶前位移以此来降低轨道复杂度。

表1 算例1水平段靶点坐标表

表2 待选平台坐标表

表3 给定待选平台位置时平台优化结果对比表

表4 算例2水平段靶点坐标表

图4 给定待选平台位置时平台优化结果图

优化计算结果如表5和图5所示。图5中，绿色区域为待选平台位置的可行区间，红色区域表示优化的平台位置。图5-a为考虑学习效应的平台优化结果，而图5-b为不考虑学习效应的平台优化结果。从图5中可以看出，考虑学习效应后8口井可以由一个平台钻完；而不考虑学习效应的结果为每个平台钻4口井。考虑学习效应的建井总费用为672.7万美元，相对于不考虑学习效应的建井总费用899.3万美元，总费用减少25%。此外，优化模型能够避免大鱼钩井的出现，从而降低钻井作业难度。

表5 给定待选平台可行区域时平台优化结果对比表

图5 给定待选平台可行区域时平台优化结果图

5 结论

1）在“井工厂”模式下，钻井学习效应、平台容量和轨道复杂度等因素能够显著影响丛式水平井平台位置的选择和钻井费用。考虑钻井学习效应的平台优化模型能够减少平台数量，增加每个平台的钻井数量，更有利于应用“井工厂”技术从而降低钻井费用。

2）丛式水平井平台优化为数学上的最优化问题，可根据遗传算法的原理进行快速求解。采用遗传算法求解所建立的模型时，在进行编码、交叉和变异设计中需考虑井与平台的对应关系；在适应度函数设计中，罚函数法是处理平台容量和轨道复杂度等约束的一种有效方法。

[1] Devine MD & Lesso WG. Models for the minimum cost development of offshore oil ベelds[J]. Management Science, 1972, 18(8):B-378-B-387.

[2] Dogru S. Selection of optimal platform locations[J]. SPE Drilling Engineering, 1987, 2(4): 382-386.

[3] 史玉才, 管志川, 陈秋炎, 周延军. 钻井平台位置优选方法研究[J]. 中国石油大学学报(自然科学版), 2007, 31(5): 44-47.Shi Yucai, Guan Zhichuan, Chen Qiuyan & Zhou Yanjun. Location optimization method for drilling platform[J]. Journal of China University of Petroleum (Edition of Natural Science), 2007,31(5): 44-47.

[4] 李文飞, 朱宽亮, 管志川, 陈明, 刘云鹏, 史玉才. 大型丛式井组平台位置优化方法[J]. 石油学报, 2011, 32(1): 162-166.Li Wenfei, Zhu Kuanliang, Guan Zhichuan, Chen Ming, Liu Yunpeng & Shi Yucai. Location optimization for the drilling platform of large-scale cluster wells[J]. Acta Petrolei Sinica, 2011, 32(1):162-166.

[5] Grimmett TT & Startzman RA. Optimization of offshore ベeld development to minimize investment[J]. SPE Drilling Engineering,1988, 3(4): 403-410.

[6] 陈祖锡, 葛云华, 周煜辉. 用丛式井开发油田的方案设计[J].石油钻采工艺, 1992, 14(6): 19-28.Chen Zuxi, Ge Yunhua & Zhou Yuhui. Schematic design for oilベeld development with cluster wells[J]. Oil Drilling & Production Technology, 1992, 14(6): 19-28.

[7] Garcia-Diaz JG, Startzman R & Hogg G. A new methodology for minimizing investment in the development of offshore ベelds[J].SPE Production & Facilities, 1996, 11(1): 22-29.

[8] 葛云华, 鄢爱民, 高永荣, 唐雪平. 丛式水平井钻井平台规划[J]. 石油勘探与开发, 2005, 32(5): 94-100.Ge Yunhua, Yan Aimin, Gao Yongrong & Tang Xueping. Drilling pad optimization for oilfield development by cluster horizontal wells[J]. Petroleum Exploration and Development, 2005, 32(5):94-100.

[9] Rodrigues HWL, Prata BA & Bonates TO. Integrated optimization model for location and sizing of offshore platforms and location of oil wells[J]. Journal of Petroleum Science and Engineering, 2016, 145: 734-741.

[10] 刘震, 潘斌, 王连宝. 海上油田中心平台选址优化[J]. 中国海洋平台, 2002, 17(2): 28-30.Liu Zhen, Pan Bin & Wang Lianbao. Position optimization for central platform of offshore oilベeld[J]. China Offshore Platform,2002, 17(2): 28-30.

[11] 王敏生, 光新军. 页岩气“井工厂”开发关键技术[J]. 钻采工艺, 2013, 36(5): 1-4.Wang Minsheng & Guang Xinjun. Key technologies of shale gas development by "well factory"[J]. Drilling & Production Technology, 2013, 36(5): 1-4.

[12] 郑力会, 魏攀峰, 张铮, 聂帅帅, 楼宣庆, 崔可心, 等. 联探并采: 非常规油气资源勘探开发持续发展自我救赎之路[J]. 天然气工业, 2017, 37(5): 126-140.Zheng Lihui, Wei Panfeng, Zhang Zheng, Nie Shuaishuai, Lou Xuanqing, Cui Kexin, et al. Joint exploration and development: A self-salvation road to sustainable development of unconventional oil and gas resources[J]. Natural Gas Industry, 2017, 37(5): 126-140.

[13] 李鹴, King-Kai H, Franks T, 谢明华. 四川盆地金秋区块非常规天然气工厂化井作业设想[J]. 天然气工业, 2013, 33(6): 54-59.Li Shuang, King-Kai H, Franks T & Xie Minghua. Design highlights of factory-like production of unconventional natural gas wells in the Jinqiu Block, Sichuan Basin[J]. Natural Gas Industry,2013, 33(6): 54-59.

[14] 刘社明, 张明禄, 陈志勇, 梁常宝, 范文敏. 苏里格南合作区工厂化钻完井作业实践[J]. 天然气工业, 2013, 33(8): 64-69.Liu Sheming, Zhang Minglu, Chen Zhiyong, Liang Changbao& Fan Wenmin. Factory-like drilling and completion practices in the joint gas development zone of the South Sulige Project[J].Natural Gas Industry, 2013, 33(8): 64-69.

[15] 赵文彬. 大牛地气田DP43水平井组的井工厂钻井实践[J]. 天然气工业, 2013, 33(6): 60-65.Zhao Wenbin. Drilling practice of a well plant in the cluster horizontal wells of DP43 in the Daniudi Gas Field, Ordos Basin[J].Natural Gas Industry, 2013, 33(6): 60-65.

[16] 王万庆, 石仲元, 付仟骞. G0-7三维水平井井组工厂化钻井工艺[J]. 石油钻采工艺, 2015, 37(2): 27-31.Wang Wanqing, Shi Zhongyuan & Fu Qianqian. Factory drilling technology for G0-7 3D horizontal well group[J]. Oil Drilling &Production Technology, 2015, 37(2): 27-31.

[17] 郑力会, 陈必武, 张峥, 汤继丹, 孙昊. 煤层气绒囊钻井流体的防塌机理[J]. 天然气工业, 2016, 36(2): 72-77.Zheng Lihui, Chen Biwu, Zhang Zheng, Tang Jidan & Sun Hao.Anti-collapse mechanism of the CBM fuzzy-ball drilling ぼuid[J].Natural Gas Industry, 2016, 36(2): 72-77.

[18] 郑力会, 魏攀峰, 楼宣庆, 孙昊, 付毓伟, 聂帅帅. 氯化钾溶液浓度影响页岩气储层解吸能力室内实验[J]. 钻井液与完井液, 2016, 33(3): 117-122.Zheng Lihui, Wei Panfeng, Lou Xuanqing, Sun Hao, Fu Yuwei& Nie Shuaishuai. Laboratory experiments on the effect of KCl concentration on desorption capacity of reservoir rocks[J]. Drilling Fluid & Completion Fluid, 2016, 33(3): 117-122.

[19] Ikoku CU. Application of learning curve models to oil and gas well drilling[C]//SPE California Regional Meeting, 12-14 April 1978, San Francisco, California, USA. DOI: http://dx.doi.org/10.2118/7119-MS.

[20] Brett JF & Millheim KK. The drilling performance curve: A yardstick for judging drilling performance[C]//SPE Annual Technical Conference and Exhibition, 5-8 October 1986, New Orleans,Louisiana, USA. DOI: http://dx.doi.org/10.2118/15362-MS.

[21] 胡运权. 运筹学教程[M]. 2版. 北京: 清华大学出版社, 2003.Hu Yunquan. Operational research course[M]. 2nded. Beijing:Tsinghua University Press, 2003.