星敏感器在轨光行差修正方法研究

，，， ，，

(1.上海航天控制技术研究所，上海 200233；2.上海市空间智能控制技术重点实验室，上海 201109)

0 引言

姿态测量是航天器飞行的重大核心技术，对保证航天器准确入轨和变轨、高性能飞行、可靠对地通信、高精度对地观测，及顺利完成各种空间任务具有重要意义。星敏感器是实现航天器自主姿态测量的核心部件，其测量精度直接影响姿态测量的精度。随着航天技术的发展，对航天飞行器姿态测量精度提出了更高的要求。因此对星敏感器的误差源进行分析和修正则尤为重要。而光行差是慢变误差中主要的误差来源。

目前，国内外已进行光行差修正的星敏感器普遍采用的方法是[1-2]，根据星载计算机提供的卫星轨道信息或线速度信息，在星敏感器内部对每个定姿星点进行光行差修正。该方法的缺点是可能会泄露某些保密型号卫星的轨道信息。而本文根据光行差产生的原理和特点，将星敏感器沿探测器X和Y方向产生的光行差误差角巧妙地转换为光行差误差四元数，可在星敏感器输出的四元数上直接进行修正，无须给星敏感器提供卫星轨道信息，从而为修正星敏感器光行差提供了一种方便简洁的方法。

1 星敏感器测量原理

星敏感器的测量模型[3-4]如图1所示。

图1 星光矢量测量模型Fig.1 Starlight vector measurement model

恒星P在星敏感器的焦平面上像点的坐标为(x,y)，星敏感器坐标系按照图中指向，则星光矢量SP在星敏感器坐标系中可表示为

(1)

其中，f为光学系统焦距。

同时，恒星P在地心惯性系下的矢量r由存储在导航星表中的赤经、赤纬(α,δ)表示为

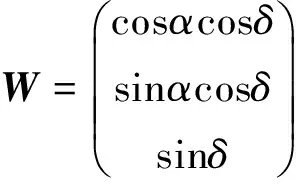
(2)

星敏感器姿态确定所依据的基本方程为

V=A·W

(3)

其中，A表示星敏感器相对于地心惯性系的方向余弦阵。当星敏感器在一帧星图中识别或者跟踪多颗恒星,利用最小二乘法获得最优的转换矩阵A，由A计算得到星敏感器测量系相对于地心惯性系的姿态四元数。

2 光行差产生原理和特点

由上述星敏感器的测量原理可知，V和W的测量误差以及转换矩阵A在转换过程中的误差都将影响星敏感器的测量精度。为此，须将影响星敏感器精度的因素进行分类，更好地将其抑制或减小，从而提高其测量精度。

根据星敏感器的测量模型以及国内外相关文献[5-6]可知，影响其精度的因素主要有：系统偏差(Bias)、慢变误差(LFE)、噪声等效角(NEA)。其中，光行差是慢变误差中主要的误差源，因此，本文对光行差进行了具体分析。

所谓光行差，是由于光传播时间以及星敏感器的线性运动，使得恒星在测量坐标系中的位置产生偏移的一种测量误差，如图2所示。假设在星敏感器探测面方向上有一个线性匀速运动，那么就可以计算出相对偏移误差。

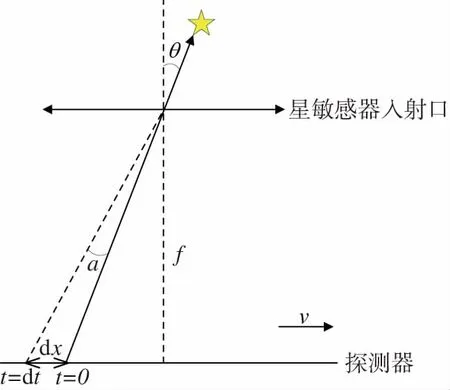
图2 光行差误差示意图Fig.2 Aberration error model

由图2可知，光束传播使得光轴和星敏感器入射口与探测器垂线之间产生一个夹角θ，光束传播的时间表达式如下

(4)

式中，c为光速，f为光学镜头的焦距，在光传播的时间内，探测器也将移动一定的位移，位移表达式如下

(5)

因此，星点在探测器上的位置也将产生dx的误差，从而会产生一个等效的角度误差a。

而由于星点离探测器的距离相当远，即角度θ足够小趋于0，sinθ=tanθ≈θ(rad)，θ角所对的边也极小，边长等于θ角所对的弧长，而θ角弧度值等于弧长比半径，即θ角等于三角形对边比临边。

(6)

因此根据式(5)和式(6)，可以得出

(7)

由式(7)可知，光行差与探测器的线速度成正比。地球公转的线速度约为v=30km/s，光速c=300000km/s。因此，根据式(7)可得出地球公转引起的光行差a1

(8)

式(8)表明，在没有修正的情况下，地球绕太阳的公转将产生21″的角度误差。

以地球同步高轨卫星为例，卫星绕地球的线速度约3.08km/s，根据式(7)可得出高轨卫星绕地球转动引起的光行差a2

0.00059°≈2″

(9)

以轨道半径为7000km的低轨同步卫星为例，角速度ω=0.06(°)/s，因此其线速度约为7.33km/s，根据式(7)可得出低轨卫星绕地球转动引起的光行差a3

0.00059°≈5″

(10)

由式(9)和式(10)可知，由于地球公转运动和卫星绕地球的运动，在低轨情况下光行差将使星敏感器产生近16″～26″的误差，高轨时光行差将使星敏感器产生近19″～24″的误差。

3 在轨光行差修正实施过程

在轨光行差修正实施过程如下：

1)计算卫星相对太阳的线速度

①计算t时刻的真近点角fs

其中，Ms为太阳视运动轨道平近点角，es为太阳视运动轨道偏心率。

②计算t时刻地球相对太阳的线速度Ve

Ve= -29788.8×

其中，ωs为太阳视运动轨道近地点幅角。

③计算卫星相对太阳的线速度在2000.0惯性坐标系的投影分量VJ2000

其中，ε为太阳视运动轨道倾角，v=(vx,vy,vz)为卫星相对地球线速度在J2000.0坐标系的投影分量，由轨道参数计算得到，单位m/s。

VJ2000的四元数表达方式为Q(VJ2000)=[0VJ2000(x)VJ2000(y)VJ2000(z)]T。

2)计算星敏感器的惯性指向

采集t时刻星敏感器四元数Q，即可计算出星敏感器的惯性指向。其中，Q=[q0q1q2q3]T。

3)计算线速度在星敏感器测量坐标系中的分量Vss

Q(Vss)=Q*⊗Q(VJ2000)⊗Q

其中，Q*=[q0-q1-q2-q3]T，Q(Vss)=[0VSS(x)VSS(y)VSS(z)]T，⊗ 为四元数相乘。

4)计算光行差误差角α

其中,C为光速，大小为3.0×105km/s。

计算星敏感器X轴线速度VSS(x)所引起的光行差误差角αx

计算星敏感器Y轴线速度VSS(y)所引起的光行差误差角αy

5)计算星敏感器光行差误差修正后四元数Q′

计算星敏感器光行差误差四元数ΔQ

计算星敏感器修正后四元数Q′

Q′=Q⊗ΔQ

4 对某星敏进行光行差修正分析

根据某在轨卫星星敏感器的在轨数据，并按上述星敏感器在轨光行差修正实施过程，分析了星敏感器光行差修正对定姿精度的影响。

由图3～图5可知，光行差对卫星定姿精度有较大影响，不修正会引起卫星约5″～11″定姿误差。因此，对于有高精度定姿要求的卫星，光行差是必须进行修正的。

图3 未修正光行差姿态角Fig.3 Attitude angle with no aberration correction

图4 修正光行差姿态角Fig.4 Attitude angle with aberration correction

图5 光行差引起的姿态偏差Fig.5 Attitude deviation caused by light difference

5 结论

本文基于光行差产生的原理和特点，将星敏感器沿探测器X和Y方向产生的光行差误差角巧妙地转换为光行差误差四元数，并直接对输出四元数进行修正，并按该方法对某在轨星敏感器进行了光行差修正前后数据比对分析，得出了光行差对卫星定姿精度的影响，从而为修正星敏感器光行差提供了一种方便简洁的方法。

[1] 奚伯齐, 李葆华, 温奇咏,等. 一种星敏感器在轨光行差的修正方法, CN 102252673 A [P]. 2011: 1-7.

[2] 张广军. 星图识别[M]. 北京: 国防工业出版社, 2010: 1-16.

[3] 李杰. APS星敏感器关键技术的研究[D].吉林: 中国科学院研究生院(长春光学精密机械与物理研究所), 2005.

[4] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1997: 1-36.

[5] 屠善澄. 卫星姿态动力学与控制[M]. 北京: 中国宇航出版社, 2005: 122-132.

[6] AA-star for high performance.

[7] 孙亚辉, 耿云海, 王爽. 星敏感器像平面移位误差的分析与校正[J]. 红外与激光工程, 2014, 43(10):3321-3328.

[8] 王永胜, 王宏力, 刘洁梁,等. 星敏感器误差模型及参数分析[J]. 电光与控制, 2014, 21(2):85-89.

[9] 孙婷, 邢飞, 尤政. 高精度星敏感器光学系统误差分析[J]. 光学学报, 2013, 33(3):253-261.

[10] 赖育网, 谷德峰, 刘俊宏,等. 星敏感器/陀螺在轨系统误差分析与校准[C]// 高分辨率对地观测学术年会分会, 2014.

[11] 熊凯, 宗红, 汤亮. 星敏感器低频误差在轨校准方法研究[J]. 空间控制技术与应用, 2014, 40(3):8-13.

[12] 熊凯, 汤亮, 刘一武. 基于地标信息的星敏感器低频误差标定方法[J]. 空间控制技术与应用, 2012, 38(3):11-15.

[13] 徐樱, 吴德安, 汪礼成,等. 星敏感器慢变误差校准方法研究[J]. 上海航天, 2016, 33(4):63-69.

[14] 连月勇, 张超, 詹银虎,等. 天文定姿恒星视位置解算及更新算法[J]. 测绘科学, 2015, 40(12):134-139.

[15] 霍德聪, 黄琳, 李岩,等. 星敏感器在轨测量误差分析[J]. 遥感学报, 2012, 16(s1):57-60.