控制性能精确可控的自适应鲁棒容错控制方法研究
2018-02-01,,远
, ,远
(1. 西北工业大学 航天学院,西安710072;2. 中国科学技术大学 自动化系,合肥 230027)
0 引言
鲁棒控制理论通常是以牺牲一定的控制性能为代价换取对干扰及未建模动态的鲁棒性,最优控制通常则是以牺牲鲁棒性为代价换取控制性能的最优,如何设计一种方法使控制系统能更好地兼顾控制性能和鲁棒性是控制领域的一个研究热点。针对这一问题,本文以容错控制系统为切入点,将参数空间方法、变结构理论,以及模型参考自适应理论相结合,尝试给出一种可行的方法,在提高系统对故障诊断误差鲁棒性的同时,又保证具备期望的控制性能。
文中拟将参数空间方法作为内回路,是因为这种鲁棒控制方法有一个很好的特点:既可以基于极点配置理论完成适应精确控制性能要求的控制系统设计,又可以基于区域极点配置理论完成适应具有一定鲁棒性且控制性能可控的控制系统设计。基于参数空间的容错控制文献很多,例如参考文献[1]针对直接力/气动力复合控制导弹,采用参数空间方法和变结构控制理论完成了复合控制系统设计。参考文献[2]基于参数空间法的区域极点配置理论研究了线性离散不确定系统在圆形区域极点约束下的容错控制问题,类似的还有文献[3]和文献[4]。
外回路拟采用变结构+模型参考自适应的方法,主要用来增加控制系统对故障诊断误差的鲁棒性。模型参考自适应的相关文献很多,例如文献[5-7]。这类方法的优点是具有较好的鲁棒性,但由于完全没有利用被控对象的模型信息,因此系统性能会受到一定影响。
下面具体介绍如何设计一个内部采用参数空间,外部采用变结构+模型参考自适应方法的自适应鲁棒容错控制系统。
1 自适应鲁棒容错控制系统设计
1.1 基本设计步骤
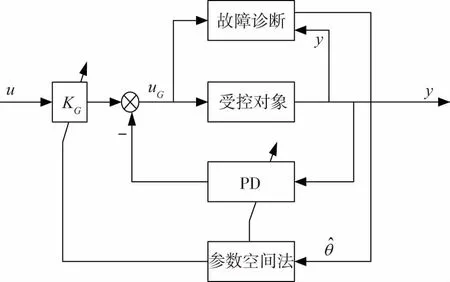
图1 基于参数空间法的内回路框图Fig.1 Block diagram of inner loop basedon parameter space method
自适应鲁棒容错控制系统内回路准备采用参数空间容错方法进行设计,外回路采用变结构+模型参考自适应控制(简称为VS-MRAC)进行设计,其框图分别如图1和图2所示。
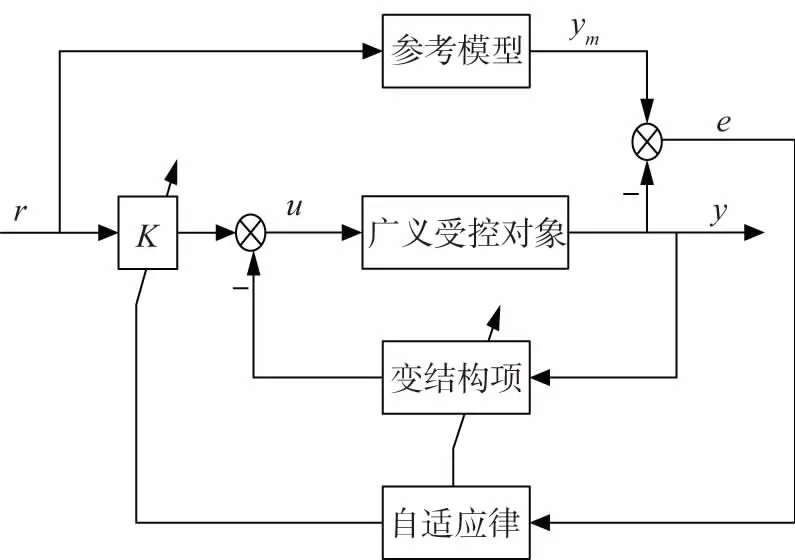
图2 基于变结构模型参考自适应的外回路框图Fig.2 Block diagram of outer loop based on variablestructure model reference adaptive
自适应鲁棒容错控制系统基本设计步骤如下:
1)进行故障模式划分,并建立包括正常模式在内的多模系统;
2)确定不同模式对应的性能指标及在零极点复平面对应的性能区域;
3)基于区域极点配置理论完成图1对应的内回路设计,给出不同模式对应的控制参数,作为图1的调参规律;
4)给定图2所示的参考模型;
5)完成图2中的控制律形式确定及自适应律的设计。
上面的基本步骤中,步骤1)~3)是图1对应的参数空间内回路设计,步骤4)~5)是图2对应的自适应外回路设计。
1.2 参数空间内回路设计与分析
以无人机一侧舵面破损故障下的纵向增稳回路设计为例给出具体设计过程,图3所示为纵向增稳回路框图。
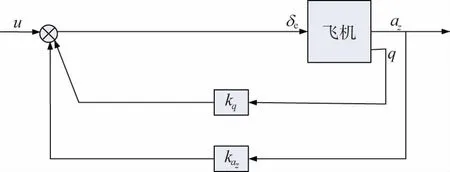
图3 无人机纵向增稳回路框图Fig.3 Block diagram of longitudinal stability loop of UAV
设计步骤如下:
1)建立多模系统
按舵面破损程度,将对象划分为正常、半损、全损3个模式,对应多模系统表示如下
i=0,1,2
(1)
(2)

2)给出一级品质和二级品质两种性能区域要求,控制系统应尽量满足一级品质,最低满足二级品质。
一级品质为ξ1≤ξ≤1,ω1≤ωn≤ω2。


3)利用网格法将性能区域划分为若干个点,每个点代表了一组ξ和ωn,利用极点配置理论可以得到每个模式下的参数集合,示意图如图4所示。

图4 参数空间示意图Fig.4 Schematic diagram of parameter space
根据不同模式参数集合的交集情况,选择合适的控制律。
至此,完成了参数空间内回路的设计。
1.3 自适应控制外回路设计与分析
自适应控制外回路设计步骤如下:
1)选择参考模型
选择一级品质中的一组ξ和ωn来确定参考模型的分母,增益则参考正常模式下的闭环增益给出,如下所示
(3)
2)图2中的控制律设计
广义受控对象即为图1所示的闭环控制系统,其传递函数如下
(4)

令
(5)
则广义受控对象可描述为如下的状态方程
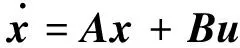
(6)
对式(3)所示的参考模型,令
(7)
则参考模型可描述为如下的状态方程
(8)
定义误差向量为
e=x-xm
(9)
对式(9)求导可得误差系统状态方程为
(10)
由于可能存在的模型故障,式(10)中的矩阵A和B为不确定参数矩阵,可记为
A=A0+ΔA,B=B0+ΔB
(11)
其中,A0和B0是正常情况的标称值,由式(4)可知,此时广义受控对象应该完全逼近式(3)所对应的参考模型,即
A0=Am,B0=Bm
(12)
另外,假设ΔA和ΔB满足匹配条件
ΔA=B0E,ΔB=B0F
(13)
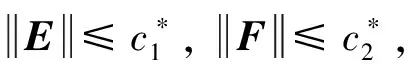
式(10)给出的误差系统状态方程可改写为
(14)
VS-MRAC的目的是使误差趋于0,即

(15)
针对误差系统状态方程式(14)设计滑模面为
s=Ge
(16)
选择Lyapunov函数为
(17)
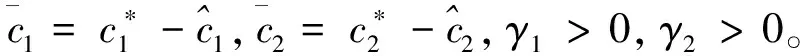
对式(17)求导可得
=eTGTG[Ame-Bmr+Bmu+ΔAx+ΔBu]-
≤eTGTG[Ame-Bmr+Bmu]+
(18)
提出如下控制律
u=ueq+uvs
(19)
式中,ueq=Ke·e+r,e=x-xm
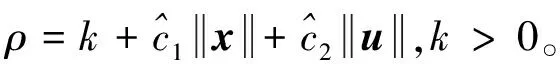

(20)
(21)
至此,完成了自适应控制外回路的设计,也完成了整个复合自适应容错控制系统的设计。
2 数值仿真
以无人机为例,受控对象相应参数如下:
一级品质为0.7≤ξ≤1,2≤ωn≤2.6。
二级品质为0.3≤ξ≤1,0.4≤ωn≤2.6。
在上面的条件下,可分别得到一级品质下和二级品质下不同故障模式的参数空间如图5和图6所示。

图5 不同故障时一级品质公共控制器参数空间Fig.5 Parameter space of common controller with firstgrade quality for different faults

图6 不同故障时二级品质公共控制器参数空间Fig.6 Parameter space of common controller with secondgrade quality for different faults
分析图5和图6可知,不存在使正常、半损和全损三种模式都为一级品质的公共控制器,但是存在一个参数交集,使得正常和半损模型下为一级品质,全损模式为二级品质。此处控制参数选择如下:
正常及半损故障时,kaz=-0.03,kq=-3。
全损故障时,kaz=-0.06,kq=-3。
此时故障诊断模块只要能分清正常和全损模式即可。
一级品质中,选择ξ=0.7和ωn=2.2,与正常模式对应的控制参数一起代入式(3),可得参考模型如下
MRAC中,控制相关的参数如下:
Ke=[4 0],γ1=γ2=0.03,G=[1 0],k=3。
假定无人机处于全损模式,当故障诊断正确时,内回路控制参数为kaz=-0.06,kq=-3,阶跃响应如图7所示,对应自适应控制指令如图8所示。
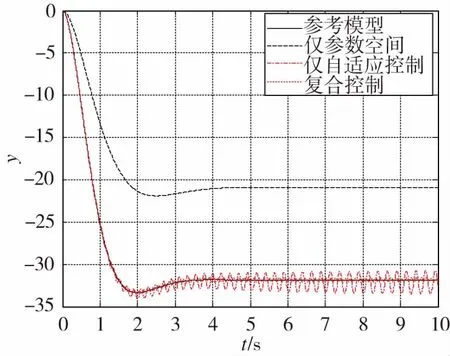
图7 诊断正确时的阶跃响应Fig.7 Step response in correct diagnosis

图8 诊断正确时变结构模型参考自适应控制的控制指令Fig.8 Control command of VS-MRAC in correct diagnosis
从图7可以看出,故障诊断正确时,单纯参数空间法仅能保证性能满足一级品质,但与参考模型规定的品质仍有差距,复合自适应控制与参考模型输出基本吻合,单纯VS-MRAC性能略差。从图8可以看出,虽然复合自适应控制与单纯VS-MRAC阶跃响应基本相同,但从控制指令来看,显然复合自适应控制从最优的角度来说能量更省。
下面,再考虑诊断存在误差的情况,无人机仍处于全损模式,故障诊断模块误诊为半损状态,此时控制增益选择kaz=-0.03,kq=-3,阶跃响应如图9所示,对应自适应控制指令如图10所示。

图9 诊断有误时的阶跃响应Fig.9 Step response with diagnosis error
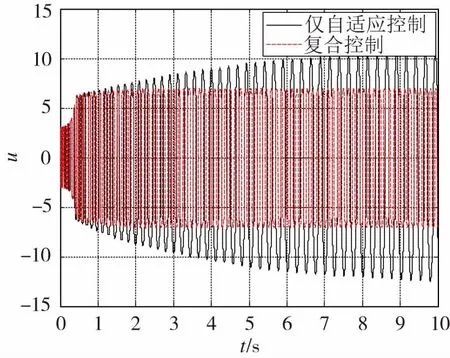
图10 诊断有误时变结构模型参考自适应控制的控制指令Fig.10 Control command of VS-MRAC with diagnosis error
从图9可以看出,故障诊断有误差时,复合自适应控制的输出最接近参考模型输出,下来是VS-MRAC,单纯参数空间方法较差,这与理论是相符的。从图10可以看出,从能量最省的角度,复合自适应控制要明显优于单纯的VS-MRAC。
3 结论
本文将参数空间方法、变结构理论、以及模型参考自适应理论相结合,给出了一种新的自适应鲁棒容错控制方法,这种方法综合了参数空间、变结构及模型参考自适应的优点,既能保证对系统控制性能约束的可控性,又能保证对故障诊断误差的鲁棒性,同时控制指令能量远小于单纯变结构控制,是一种最优控制与鲁棒控制相结合的尝试,未来要做的是进一步完善该理论,将其推广到不同的应用对象。
[1] 朱学平 , 胡晓明, 张晓峰,等. 基于参数空间方法和变结构控制的直接力/气动力复合控制系统设计[J]. 计算机测量与控制, 2014(1): 288-296.
[2] 张端金, 张洛花, 苗启. 圆形区域极点配置的Delta算子系统鲁棒容错控制[C]// 第27届中国控制会议. 昆明, 2008.
[3] 徐峰, 李东海, 薛亚丽,等. 基于区间多项式稳定性理论的PID控制器[J]. 清华大学学报(自然科学版), 2003, 43(12):1642-1645.
[4] 侯玉娟. 不确定连续系统基于区域极点配置的鲁棒容错控制[J]. 渤海大学学报(自然科学版), 2007, 28(3): 245-247.
[5] 吴忠强, 朴春俊. 模型参考自适应控制理论发展综述[J]. 信息技术, 2000(7):33-35.
[6] 林岩, 毛剑琴. 具有理想跟踪特性的鲁棒变结构模型参考自适应控制[J]. 自动化学报, 1999, 25(2): 191-198.
[7] 熊柯, 夏智勋, 郭振云. 吸气式高超声速巡航飞行器飞行攻角的模型参考自适应滑模控制[J]. 航天控制, 2011, 29(2):17-22.
