风险规避供应商的双渠道供应链决策分析研究
2018-02-01贾凯睿
贾凯睿,李 波
(天津大学管理与经济学部,天津 300072)
一、相关文献综述
目前,供应链上的供应商纷纷建立自己的电子商务平台,形成直销渠道和传统零售渠道并存的双渠道局面。供应商通过直销的电子商务平台,可以直接面对市场,提升自己产品的市场份额,但也会带来直销渠道与传统零售渠道竞争冲突的问题。另外,双渠道的出现给终端消费者带来更多的渠道选择,使得市场需求波动加大。这些因素迫使供应商一方面需要不断进行生产技术研发,创新产品,满足消费者个性化需求;另一方面,需要不断调整多渠道下上下游之间的关系,如定价策略等。这显然大大增加了供应商的压力,其可能会出现风险规避行为。
因为需求的不确定和渠道的竞争加剧,风险敏感性在供应链成员的决策中有着很大的影响力(Tsay,2002)。因此,很多学者研究了供应链中零售商具有风险规避行为时对供应链决策分析的影响。如Li等构建了一个风险中性的供应商和一个风险规避的零售商的纳什博弈模型,他们的分析表明产品定价会随着零售商的风险厌恶程度上升而提高;而制造商的直销渠道利润可能会随着零售商的风险厌恶程度上升增加或减少。Ma等也考虑了零售商的风险规避行为,探索了双方谈判能力如何在传统供应链中影响供应链成员的决策及利润分享问题。发现在制造商参与了纳什博弈(拥有与零售商对等或不对等的谈判能力)或作为Stackelberg博弈的领导者时,其分享的利润随着零售商风险厌恶程度的增加而减少。Choi等基于零售商风险态度和供应链风险态度,分别研究了制造商如何通过调整批发价和退货价进行渠道协调的决策。Gan等讨论了零售商风险规避情形下的风险共享契约,指出不能仅仅通过收入共享或回购协议来协调供应链。Xiao等使用均值方差方法探究了当面对外部供应链竞争时,供应商如何通过设计批发价使零售商披露自己的风险厌恶水平,以及对双方价格决策的影响。马利军等通过构建Nash博弈模型,研究了当需求波动且为乘法需求模型时,供应商与风险规避零售商的博弈结果。王莹莉使用混合CVaR方法研究供应商如何设计回购协议进行供应链协调,发现不论零售商的风险偏好系数大于1或小于1,设计的回购契约均可实现协调。
但以上文献均假设零售商是风险规避的,而供应商是风险中性的。目前还少有文献基于由风险规避的供应商和风险中性的零售商构成的供应链来进行研究,仅有Chyu等考虑了供应商的规避行为,使用确定等值法探究了如何设计利润共享机制将分散式供应链转变为集中式供应链,以实现帕累托改进。在分散式决策下,供应商作为领导者决定批发价,而零售商决策产品价格和订货量。进一步,基于Shen等的调查,发现供应商风险厌恶而零售商风险中性这一假设与服装行业的实践非常吻合,他们通过均值方差法度量了供应商效用,且使用折扣价政策协调供应链,最后发现,供应链的风险容忍程度以及供应商风险容忍水平对批发价和折扣价有不同的影响。
事实上,在双渠道供应链中,因为供应链除了面临生产产品的压力外,还需直接面对市场及其来自零售商的渠道竞争。因此,供应商会有风险规避行为。但目前还没有双渠道供应链下考虑供应商风险规避行为对决策策略研究影响的文献,且目前很多研究文献均采用均值方差方法来度量成员的风险规避效用。因为均值方差方法的缺陷是同等地量化上行利润和下行风险,造成其度量结果可能存在偏差;而条件风险值(Conditional Value-at-Risk,CVaR)方法不仅克服了均值方差方法的缺陷,还具有很好的计算性质。
基于以上文献成果,本文运用纳什博弈模型研究了双渠道供应链中一个风险厌恶的供应商和一个风险中性的零售商的决策行为及其均衡策略。本文采用CVaR方法来测量供应商的风险规避行为,并通过纳什博弈模型得出均衡解。发现产品价格随供应商风险厌恶程度增大而升高,但随需求波动增大而降低,且给出了供应商利润占总供应链利润份额的范围。最后,借助数值实验分析,探究了不同市场需求波动以及不同渠道替代敏感度下供应商风险厌恶程度对价格决策以及供应链成员利润的影响。
二、参数表示与基本模型
本文应用CVaR方法来测算供应商的风险规避水平,定义供应商的利润为πs,指标η表示供应商风险规避的程度,且η∈(0,1]。因此,零售商的 η-CVaR 定义为:

其中,v表示供应商的目标利润水平,η指的是供应商保持自己目标利润水平v下的风险规避因子。
在一个风险规避的供应商和一个风险中性的零售商构成的双渠道供应链中,供应商生产一种易逝产品。消费者可以无差别地从供应商的线上渠道或者零售商的传统零售渠道购买该成品。在销售期初,假设零售商采用备货型生产(make-to-stock)方式,因为基于他对市场长期的丰富经验,可以较准确地预测未来的市场需求。而供应商在其直销渠道采用订单型生产(make-to-order)方式应对需求波动。事实上,采用这种混合策略的文献十分丰富。例如,Adan等就探究了两种策略的结合如何影响生产提前期的问题;而Carr等在混合备货型生产和订单型生产生产系统中扩展了物料入场控制与排队的理论。
本文中的参数表示如下:i为标号,i=S代表供应商;i=B代表零售商;ps和pB为供应商直销渠道和零售渠道每单位产品的价格;q为在销售期初,零售商向供应商发出的产品订货量;w为供应商制定的每单位产品的批发价;c为供应商生产单位产品的成本;D为基本市场需求;ξ为产品需求的不确定性,是一随机变量,其概率密度函数和累计分布函数分别为φ(·)和 Φ(·)。本文假设 φ(·)服从[-U,U]的均匀分布,0≤U≤D为总的市场需求,满足D=D+ξ;θ为线下零售市场的市场份额,且0≤θ≤1,则1-θ是供应商线上销售的市场份额;bs和bB为渠道的价格弹性系数;a为两渠道之间的交叉价格弹性,代表两个渠道之间的替代程度,满足bs≥a,bB≥a,表示渠道自身的产品价格比另一个渠道的产品价格对本渠道需求的影响大;πi为供应链双方的利润,i=S,B;μs为供应商的利润占供应链总利润的份额,即
在销售周期前,供应商以单位产品c的成本进行备货生产;到销售季初,供应商制定产品的批发价w,则零售商基于制造商给出的批发价w向供应商订购q件产品。然后,供应商制定其在直销渠道的销售价格ps。这里,假设两个渠道的销售价格p>w>c,且因为是易逝品,销售剩余的产品残值不再考虑。
则线上和线下两渠道的需求可以假设满足以下价格依赖需求的函数形式:

其中,D是常数,代表基本的市场需求。ξ是随机数,代表需求的不确定性。本文假设ξ服从[-U,U](0≤U≤D)的均匀分布,概率密度函数和累计分布函数分别是φ(ξ)和Φ(ξ)。
为了避免双渠道的激烈竞争,这里假设供应商的直销渠道的销售价格同零售商的销售价格一致,即Ps=PB=p,则以上的需求函数可以简化为:


其中,γB=bB-a,γs=bs-a,这里γ代表两渠道的替代敏感系数。
基于Nash博弈模型,假设供应商和零售商拥有同等的议价能力,建立该问题的纳什博弈模型如下:

其中,πs0表示供应商的保留利润,πB0表示零售商的保留利润。供应商和零售商在正常情性下都均需要保持他们的保留利润。假设双方的保留利润都是0,且这个假设对本文的后续分析没有影响,且这种假设在文献中很普遍。则,以上公式(5)可以写成如下:

三、模型分析
根据上面公式(1),可以得出供应商利润的η-CVaR效用如下:
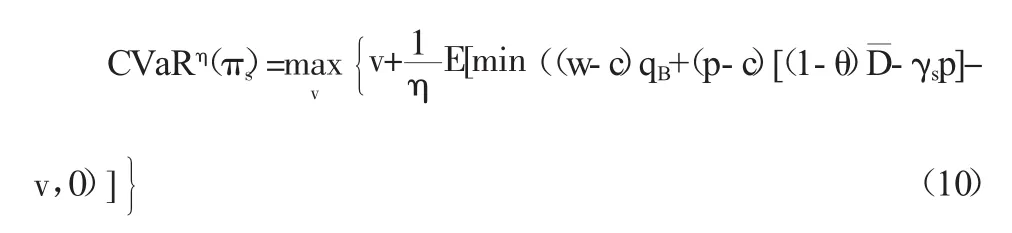
为了计算供应商的目标利润水平v,以下分三种情况进行讨论:
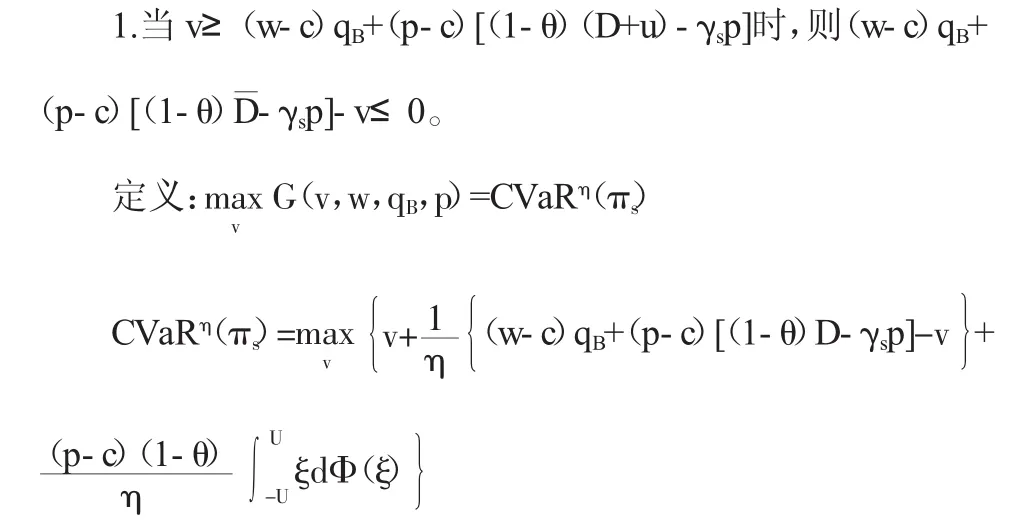
2.当(w-c)qB+(p-c)([1-θ)(D-U)-γsp]≤v<(w-c)qB+(p-c)([1-θ)(D+U)-γsp]时,则(w-c)qB+(p-c)([1-θ)γsp]-v可能是正数,也可能是负数。

因为(w-c)qB+(p-c)[(1-θ)(D-U)-γsp]≤v<(w-c)qB+(p-c)[(1-θ)(D+U)-γsp],且有:
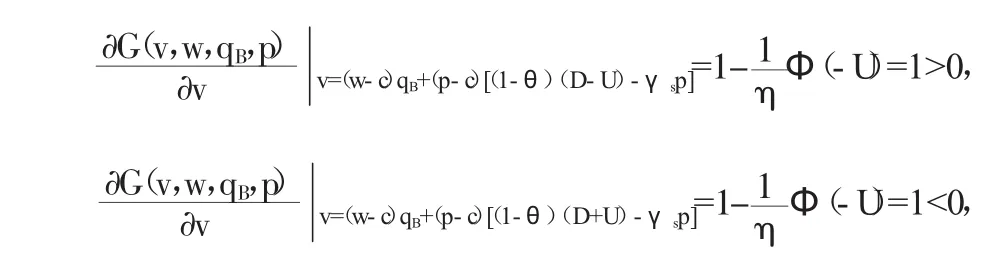
3.如果v<(w-c)qB+(p-c)([1-θ)(D-U)-γsp],则(w-c)qB+(p-c)([1-θ)γsp]-v>0。
因为前面已经讨论过v=(w-c)qB+(p-c)[(1-θ)(D-U)-γsp],这里不再赘述。
另外,因为 G(v,w,qB,p)在上连续,这种情形在第二种情况中已经考虑。因此,得出是满足CVaR方法的最优解。
依据以上的讨论,可得出以下命题1。
命题1:当供应商和零售商拥有同等谈判能力且需求的不确定性ξ服从[-U,U(]0≤U≤D)的均匀分布时,纳什博弈存在如下的均衡解(,w*,p*)。
(1)最优的线上线下价格满足以下方程:
2(γB+γS)p*3-[D+(1-θ)(η-1)u+(γB+γS)c]p*2+θUc2=0。
因为最优的线上线下价格满足一个隐函数,比较复杂。但分析其和供应商风险规避程度和市场需求的关系,可以得出命题2。
命题2:(1)随着供应商的风险规避程度增加(即η减小),最优的线上线下价格p*也降低。(2)随着市场需求波动的加剧(U增大),最优的线上线下价格p*也急剧降低。
由命题2(1)可知,随着供应商风险规避程度的增加,因为市场需求的波动性,其为了最大化其收益,会制定较高的批发价;而零售商面对趋于保守的供应商,会制定较低的销售价格来扩大销售量。但反之,随着供应商趋于风险中性,其会积极应对随机性的市场和渠道竞争,会制定较低的批发价,来提高销售量。而零售商面对供应商的积极心态,会制定较高的销售价格来最大化自己的利润。由命题2(2)可知,当市场随机性加剧时,供应商和零售商都面临着很大的需求波动性。为了规避这种需求带来的风险,扩大销售量,零售商会积极降低销售价格。这种信号传递到上游供应商处,供应商也会随之调整策略,如降低批发价,来维持和零售商的稳定合作机制,因为在纳什博弈中他们具有拥有同等谈判能力。
进一步,在该双渠道供应链中,供应商的利润占供应链的总利润情况可以得出命题3。
命题3:具有风险规避供应商的利润占双渠道供应链整体利润的份额是
命题3揭示了一个有趣的现象,就是当供应商风险中性时,即η=1,供应商和零售商的利润一致,平等分割整个供应链的利润;但当η逐渐减小时,即供应商逐渐变得越来越风险规避,则他将攫取供应链中更多的利润份额。尤其是当η=0时,即供应商极端风险规避,则他将攫取供应链的所有利润。这种情形下,零售商可能就不再参与同供应商的合作,销售关系将终止。所以命题3说明,供应商的高风险规避程度可能破坏供应链成员之间的合作关系。因为当零售商的利润远小于供应商的利润时,他会觉得“不公平”并可能拒绝与供应商进行产品销售的合作。
四、数值实验分析
这部分将进行数值实验分析来进一步讨论供应商风险规避程度与市场需求波动对双渠道供应链定价决策、成员的利润以及供应商利润份额等策略的影响。参考[3,8]等文献中有关数据的取法,这里令 γB=0.7,γS=0.5,θ=0.6,D=100,c=5。
1.需求波动的影响分析。这里分别取U=10、U=30和U=50来表示需求不确定性的不同波动情形。图1给出不同需求波动情形下对产品价格及批发价的影响关系。

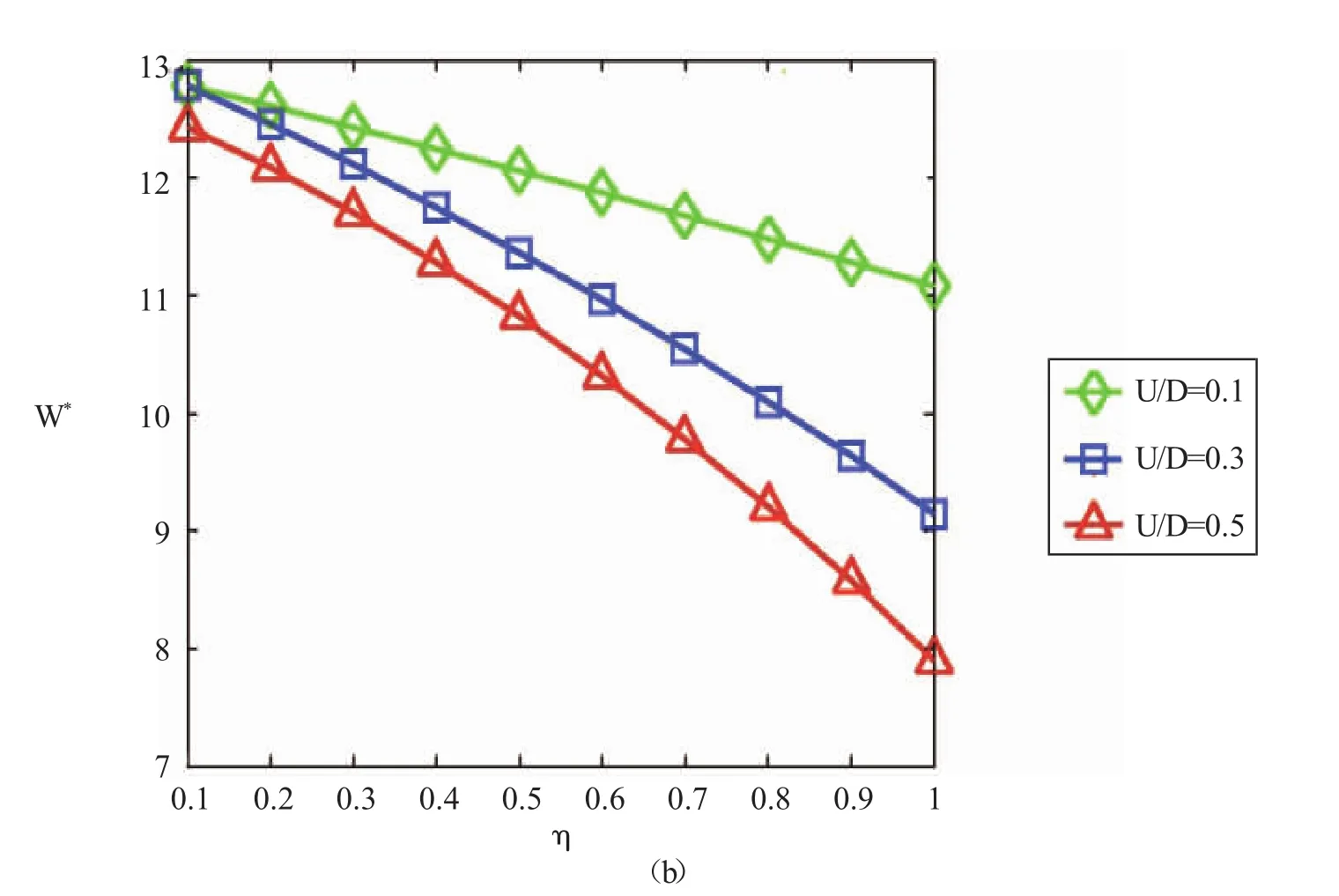
图1 不同需求波动情形下η对产品价格与批发价的影响
从图1(a)中可以得到与命题2一样的结论,即随着供应商越来越风险规避(η减小),则最优线上线下价格p*降低。进一步,发现当市场波动较大时,供应商的风险规避程度η对线上线下的价格有更大的影响,其上升或下降的陡度较大。这也与命题2的结论一致。但当供应商为风险中性时,需求波动的幅度对线上线下的价格不产生影响。图1(b)展示出当供应商风险规避程度趋于中性时,批发价将降低。即供应商越风险规避,其制定的批发价越高。进一步,当需求波动剧烈时,这种变化曲线变得更加陡峭。结合图1(a)和(b)的观察,可以发现需求的剧烈波动会恶化供应商的风险厌恶行为。
下页图2给出了不同需求波动时η对双方成员利润及供应商利润占供应链总利润比例的影响分析。从图2(a)中可以观察到一个有趣的现象:相对于较小的市场需求波动,在市场需求波动较大时,若供应商极端风险规避,则他攫取了供应链中最多的利润,而零售商的利润最低;反之,若供应商趋于中性,则他将获利最少,等于零售商的利润水平。不确定性是人们拥有风险规避态度以规避损失的原因之一,并且当人们面对不同程度的不确定性时,他们可能会通过调整自己的风险规避程度来保证自己利益的最大化。这个反馈机制也许就是极度风险规避的供应商能够在市场需求波动剧烈情形下获得更多利润。图2(b)从另一个视角为解释了供应商在市场需求高不确定性时利润分配的优势。当需求急剧波动时,供应商的利润占供应链总利润比例是最高的,结论同图2(a)。只有当供应商风险规避程度η=1时,不同的市场需求波动不会影响双方的利润占比,即双方各占50%。
2.渠道替代敏感度的影响分析。下面研究供应商的风险规避程度η在不同渠道替代敏感度下是如何影响产品定价及供应链的利润分配的。数据取值同上,令U=10。为了检验渠道替代的敏感性,取三组数据来表示不同的渠道替代敏感度,即 γB=0.5,γS=0.7,有 γB<γS;γB=0.6,γS=0.6,有 γB=γS;γB=0.7,γB=0.5,有γB>γS。下页图3给出了不同渠道替代敏感度下风险规避程度对零售商销售价格及其订货量的影响关系。
从图3(a)可以看出,不同渠道敏感度下产品价格是一致的。这个结果揭示出供应链成员合作下复杂的相互关系。如当线上渠道可替代水平高时,若零售商试图降低产品价格,那供应商将加大自己的批发价作为回应。则较高的批发价格将抵消了零售商从线下渠道获取的利润,迫使零售商降低订货量,参见图 3(b)。当 γB=0.5>γS时,零售商的订货量最低。这个比较好理解,当零售商的线下渠道更容易被替代时,他订货时会变得更保守。另一方面,随着供应商风险规避程度的增加,销售价格直线升高,但零售商的订货量略有下滑。
与图2(a)类似,本文图4(a)展示出不论渠道替代敏感度如何,供应商和零售商都将获得相同的利润,解释同前,不再赘述。进一步展示不确定性上限U对产品价格的影响,这里令η=0.7。显然由图4(b)可知命题3成立,即当零售商面临较大的市场需求波动时,产品价格降低。其次,可以注意到:不论线上线下渠道替代敏感度如何,需求波动将对产品价格施加相同的影响。
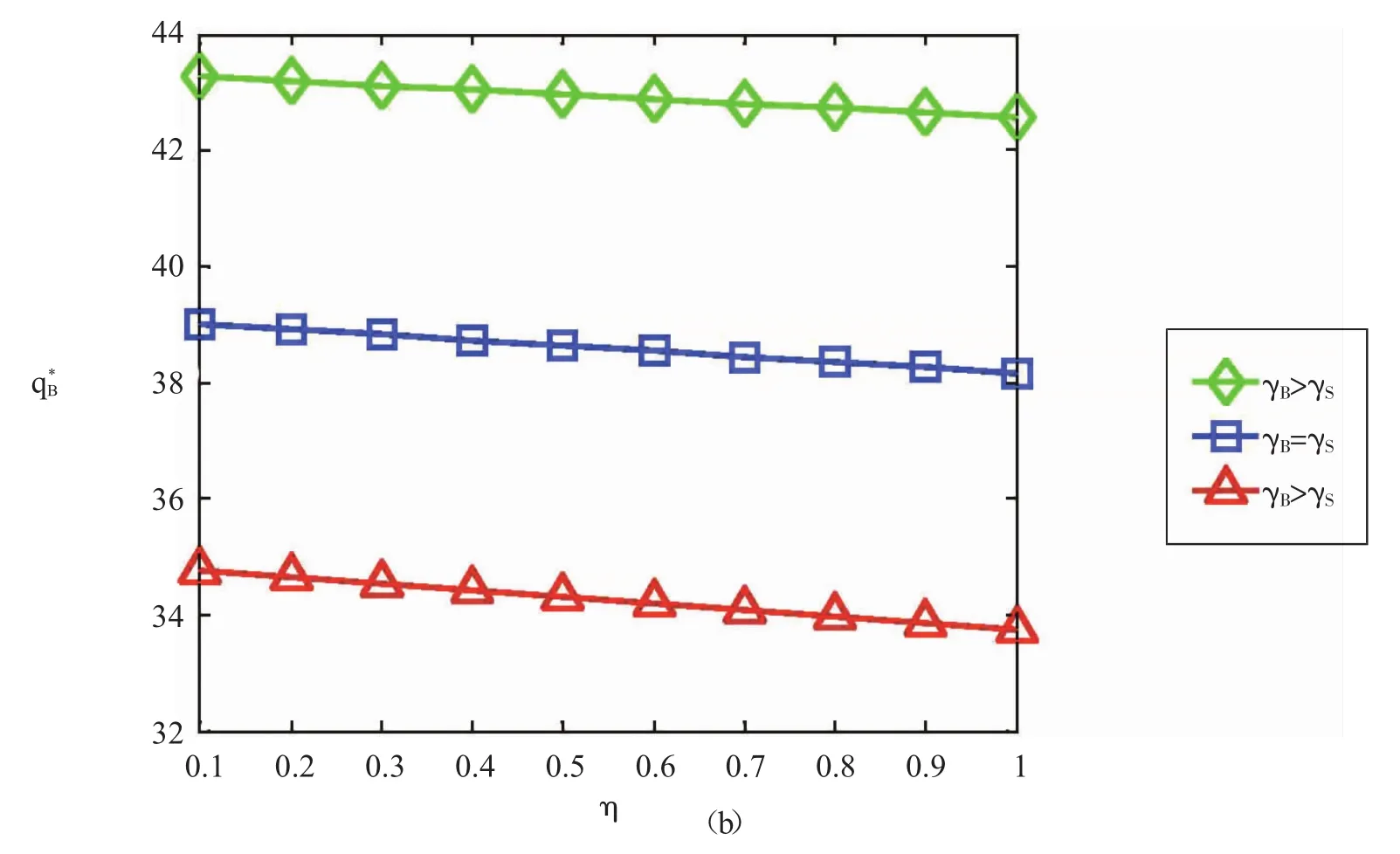
图3 不同渠道替代敏感度下η对产品价格、零售商订货量的影响
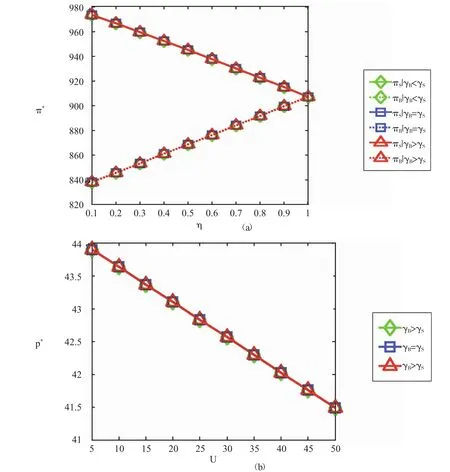
图4 不同渠道替代敏感度下η和U分别对供应链成员利润及价格的影响
五、结论
本文研究了当市场需求不确定时,由一个风险规避的供应商和一个风险中性的零售商组成的双渠道供应链系统的定价决策问题。采用CVaR方法来测量供应商的风险效用,建立了纳什博弈模型,并得出了线上线下产品价格、订货量及批发价格的均衡解。研究发现,产品价格随供应商的风险规避程度的加剧而降低,且产品价格还随需求不确定性的升高而下降。最后还给出了供应商的利润占供应链总利润份额的取值范围。最后,本文通过数值实验分析来验证了本文得出的结论。进一步发现,在不同的市场波动水平下,当供应商的风险规避程度增大时,产品价格升高,而批发价格、供应商和零售商之间的利润差额以及供应商的利润份额都会下降。换句话说,供应商将因为他的风险规避行为收益,但零售商将为此承担损失。而在不同的渠道替代敏感度下,产品价格和供应链成员的利润都保持不变,但零售商将改变他的订货量。这些管理解释,将对具有风险规避行为的供应商双渠道系统的决策分析提供参考作用。
进一步研究方向在于,一是本文考虑的是供应链双方成员具有相同谈判能力的纳什博弈模型;若供应商双方权利不对等,可能会得出不一样的结论。二是本文仅仅考虑由一个供应商和一个零售商组成的双渠道供应链系统;若是一个供应商和多个零售商组成的多渠道供应链系统,可能结论会复杂更多,这些都将是下一步研究的重要方向。
命题1的证明:
求解采用逆推法,首先求解零售商的决策变量,即:


令F(qB,w,p)=CVaRη(πs)E[πB]
为了对公式(6)求解,首先需要求解下列方程:

其中,p*满足下列方程:
(2γB+2γS)p*-([1-θ)(η-1)U+γBc+γSc+D]p*2+θUc2=0(.A1)
进一步,需要证明方程(6)在均衡解处的海赛矩阵是负定矩阵。令H、d1、d2和d3分别表示海塞矩阵和它的一阶子式、二阶子式以及三阶子式。

在均衡点(q*B,w*,p*)处,计算:

因此,就证明了方程(6)的海塞矩阵是负定矩阵,也即说明求得的均衡解是稳定的。
命题 2(1)的证明:
从命题1中得到线上线下最优的产品价格ρ满足下列方程:
(2γB+2γS)p3-[(1-θ)(η-1)U+γBc+γSc+D]p2+θUc2=0
因此,
命题 2(2)的证明:
同样利用如下方程来分析求解:
(2γB+2γS)p3-[(1-θ)(η-1)U+γBc+γSc+D]p2+θUc2=0
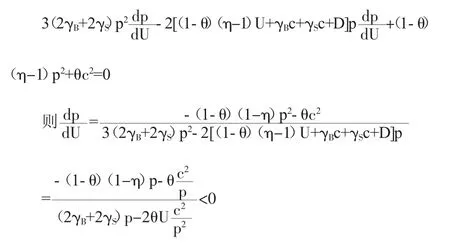
命题3的证明:
因为供应商的利润函数为:
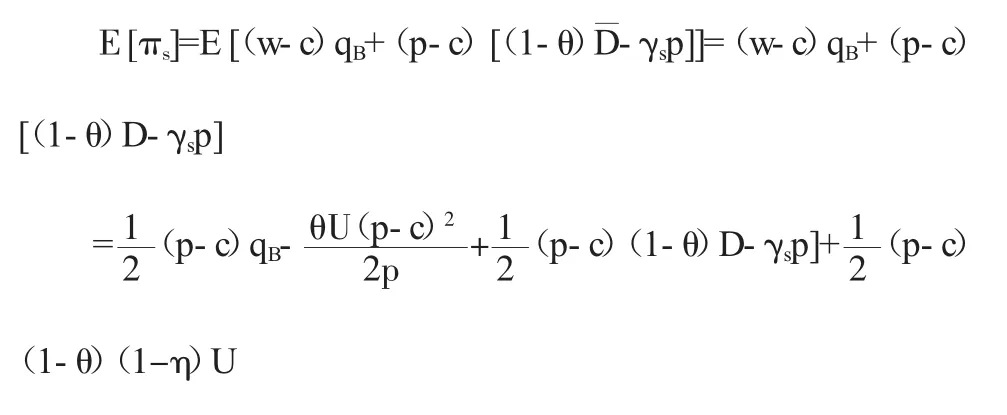
则有:


[1]Tsay,A.A.Risk Sensitivity in Distribution Channel Partnerships:Implications for Manufacturer Return Policies.Journal of Retailing,2002,(2):147-160.
[2]Bo Li,Ping Chen,Qinghua Li,Weiguang Wang.Dual-channel supply chain pricing decisions with a risk-averse retailer.International Journal of Production Research,2014,(23):7132-7147.
[3]Lijun Ma,Fangmei Liu,Sijie Li,Houmin Yan.Channel bargaining with risk-averse retailer.International Journal of Production E-conomics,2012,(13):155-167.
[4]Tsan-Ming Choi,Duan Li,Houmin Yan Chun-Hung Chiu.Channel coordination in supply chains with agents having mean-variance objectives.Omega,2008,(36):565-576.
[5]Xianghua Gan,Suresh P.Sethi,Houmin Yan.Channel coordination with a risk-neutral supplier and a downside-risk-averse retailer.Production and Operations Management,2005,(14):80-89.
[6]Tiaojun Xiao,Daqin Yang.Risk sharing and information revelation mechanism of a one-manufacturer and one-retailer supply chain facing an integrated competitor.European Journal of Operational Research,2009,(6):1076-1085.
[7]马利军,刘芳梅,周威,赵映雪.乘法需求模式下具有风险厌恶零售商的供应链合作博弈分析[J].系统科学与数学,2011,(10):306-316.
[8]王莹莉.基于混合CVaR的供应链回购策略优化与协调研究[J].系统科学与数学,2015,(11):304-315.
[9]Chiuh-Cheng Chyu,I-Ping Huang.Coordination scheme for restructuring business operation of the single period newsvendor problem.Mathematical Problems in Engineering,2013,http://dx.doi.org/10.1155/2013/308187.
[10]Bin Shen,Tsan-Ming Choi,Yulan Wang,Chris K.Y.Lo.The coordination of fashion supply chains with a risk-averse supplier under the markdown money policy.IEEE Transactions on Systems,Man,and Cybernetics:Systems,2013,(2):266-276.
[11]Jun Wu,Shouyang Wang,Xiuli Chao,C.T.Ng,T.C.E.Cheng.Impact of risk aversion on optimal decisions in supply contracts.International Journal of Production Economics,2010,(12):569-576.
[12]Ivo J.B.F.Adan,Jan van der Wal.Combing make to order and make to stock.OR Spektrum,1998,(20):73-81.
[13]Scott Carr,Izak Duenyas.Optimal admission control and sequencing in a make-to-stock/make-to-order production system.Operations Research,2000,(5):709-720.
[14]R.Tyrrel Rockafellar,Stanislav Uryasev.Optimization of conditional value-at-risk.Journal of Risk,2000,(2):21-41.
[15]Guangye Xu,Bin Dan,Xumei Zhang,Can Liu.Coordinating a dual-channel supply chain with risk-averse under a two-way revenue sharing contract.International Journal of Production Economics,2014,(14):171-179.
[16]Hisashi Kurata,Dong-Qing Yao,John J.Liu.Pricing policies under direct vs.indirect channel competition and national vs.store brand competition.European Journal of Operational Research,2007,(18):262-281.
