风险规避型零售商双渠道供应链定价策略研究
2018-01-31,,,
, , ,
(1.武汉科技大学 管理学院,湖北 武汉 430081; 2.华中科技大学 管理学院,湖北 武汉 430074)
1 引言
Internet网络塑造了一个全新的消费市场和一个不断壮大的网络用户群体,企业通过电子商务这一崭新的经营模式可以迅速获取新的竞争优势。尤其近年来,电子商务和网络零售进入快速增长期。而传统实体零售企业在经济增长放缓和电子商务冲击的背景下,面临着经营成本高、消费者流失和利润减少的严峻挑战,甚至许多传统零售业出现关门歇业现象。在这种情况下,传统零售企业开始寻求销售模式的改变,纷纷将目光投向电子商务业务模式。于是许多传统零售巨头企业,如沃尔玛、苏宁、国美等企业除了继续保留传统实体店外纷纷开通网络销售渠道,即零售商双渠道销售模式。实施双渠道销售模式,往往会导致渠道冲突,如制造商与零售商的冲突,线下和线上渠道的冲突,而缓解渠道冲突的主要手段是合理地确定双渠道的价格,因此研究零售商双渠道的定价策略意义重大。
目前,关于双渠道供应链定价方面的研究主要集中在制造商双渠道供应链方面。如Brynjolfsson和Michael[1]通过对两类同质产品书籍和光盘的实证研究发现,这两类产品在网上价格比实体店便宜9%~16%,互联网上书籍价格平均相差33%,CD价格平均相差25%。Chiang等[2]指出直销渠道有利于制造商和整个供应链,减少了价格双重边际效应,同时直销渠道并不是总有害于零售商,因为它可以降低产品批发价格。Hsieh等[3]考虑多个制造商和一个共同的零售商在供应链面临着不确定的需求时的定价和订货量决策问题。Panda等[4]探讨了一个由实体店和网络渠道组成的制造商Stackelberg双渠道供应链的定价和补货决策问题。Yao和Liu[5]构建Bertrand模型和Stackelberg模型,获得了均衡定价策略。Khouja等[6]研究了基于零售偏好型消费者情形下制造商的渠道选择和价格策略。
然而,目前关于零售商双渠道供应链定价问题的研究不多,如Wang和Liu[7]提出了一种模型,研究在零售商主导的供应链渠道期权契约合同协调和风险分担问题。Pan等[8]通过构建一个两周期模型去研究零售商主导的多周期订货决策问题。Huang和Swaminathan[9]研究了在确定需求情形下风险中性的零售商双渠道的定价策略。Zhang等[10]研究在一个由两个制造商和两个零售商组成的供应链中,分别讨论在制造商Stackelberg,零售商Stackelberg和垂直Nash三种情况下的具有替代性产品在需求确定情形下的定价策略。Wang等[11]研究了在两个制造商和一个共同的占主导地位的零售商组成的供应链的加成定价策略问题。Zhang和Wang[12]主要研究短生命周期情况下零售商双渠道的协调问题。随着市场需求不确定性的增加,企业在追求最大利润的同时必须考虑企业的风险承受能力,因此,企业对待风险的态度影响着企业的最终利润。关于供应链参与者风险的双渠道定价的文献较少。Xiao和Yang[13]研究了在需求不确定情形下零售商的风险敏感程度对服务水平和价格的影响。Xie等[14]研究了在三种不同供应链结构中的供应链参与者的风险厌恶行为,结果表明供应链结构和供应链参与者的风险态度对质量投资及定价有显著影响。Xu等[15]研究了供应链参与方是风险规避型的制造商双渠道定价策略,并提出双向的利润共享契约协调机制。Liu等[16]研究在完全信息和不对称信息情形下制造商双渠道供应链参与者的风险规避型程度对价格和利润的影响。Kim和Park[17]研究了在一个分散决策下的制造商双渠道供应链中,参与者的风险规避态度对价格的影响。Li等[18]研究了在需求不确定情况下,制造商双渠道供应链中风险规避型零售商对定价的影响。
与上述文献不同的是,本文是在考虑市场需求随机和零售商主导供应链情形下,研究风险规避型零售商双渠道供应链的定价问题。通过分别建立集中和分散决策下零售商、制造商和整个供应链的均值-方差模型,然后对两种决策模式下的定价和期望效用进行对比分析,在此基础上,深入地分析零售商风险敏感系数、需求波动程度、价格弹性系数、交叉价格弹性系数、市场份额和市场基本需求量等对零售商双渠道价格和期望效用的影响程度。
2 问题描述与模型假设
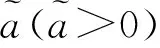
度量制造商和零售商的风险态度的方法很多,根据Choi[19]对风险规避的模型的总结,本文采取均值-方差理论来度量供应链参与方的风险态度。km、kr分别表示制造商和零售商的风险规避度,kr≥0,kr=0表示零售商属于风险中性,kr>0表示零售商对风险持规避态度,kr越大,零售商对风险越厌恶。km的理解同kr。由于假定零售商是风险规避型,制造商是风险中性型,因此km=0。
在模型中,制造商以批发价w将单位成本为c产品出售给零售商,零售商通过双渠道进行产品销售,线下和线上的销售价格分别为pr和pe,pi>w>c,(i=r,e)。需要说明的是,当零售商是供应链的领导者时,直接将p代入利润函数中不能求得最优值,此时需要将p表示为w的函数,即销售价格可以表示为批发价格的溢价部分(Δwi)加上商品的批发价格,将零售商的决策变量pi换算成Δwi,即pi=w+Δwi,其中i=r或e。
πi,E(πi),U(πi)分别表示利润、期望利润和期望效用。上标c为集中决策模式,上标d为分散决策模式,上标*为最优决策;下标r代表零售商或线下渠道,下标e代表线上渠道;下标m代表制造商,下标sc代表整个供应链。
根据以上假设条件,并采用以往学者分析模型中需求函数的形式[9],零售商的两个渠道的线性需求函数如下
(1)
(2)
其中dr表示线下渠道的需求,de表示线上渠道的需求。
3 模型构建与求解
在零售商双渠道供应链中,假定零售商是风险规避型,是供应链中的领导者,而制造商的风险偏好是中性型,在供应链中处于跟随者。为了分析零售商的风险规避态度对双渠道供应链的价格和利润的影响,现在分别考虑集中决策和分散决策下零售商和制造商的决策行为。
3.1 集中决策模式
根据已知条件知,在零售商双渠道供应链中,零售商是领导者,即供应链的产品价格和产量的决策主要由零售商来制定。当双渠道供应链由一个决策者集中控制或管理时,系统将追求整个双渠道供应链利润的最大化,在这种情形下,做出的决策是全局最优的。
根据已知条件可知,集中决策模式下整个双渠道供应链的期望利润为
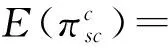
(3)
集中决策模式下整个供应链的利润方差为
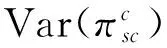
(4)
集中决策模式下整个供应链的期望效用目标函数为
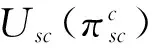
(5)
命题1集中决策模式下零售商双渠道供应链的最优定价策略分别为
(6)
(7)
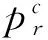
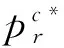
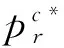
性质1说明,在集中决策模式下,双渠道供应链的领导者零售商如果是风险规避型,随着其对市场风险厌恶程度越来越高,将会有强烈的意愿去降低线下和线上渠道商品的销售价格,促进更多消费者进行购买。性质2则说明,随着越来越多的消费者偏好线下渠道时,零售商则可以通过提供更好的购物体验和服务水平来增强顾客的忠诚度,此时,可以提高线下渠道的价格,使自己利润最大化。与此相反,随着偏好线下渠道的顾客越来越多,线上渠道为了吸引更多顾客,通常会采取降价策略来分流线下渠道的顾客。
命题2集中决策模式下零售商双渠道供应链的最大期望效用为
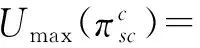
(8)
性质3在集中决策模式下,整个供应链的期望效用与零售商的风险规避kr存在如下关系:
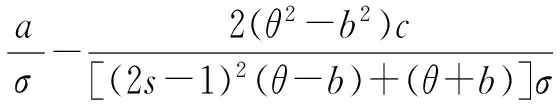
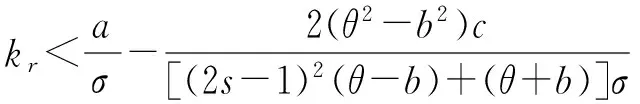
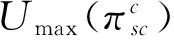
性质3说明零售商的风险规避程度影响其期望效用,当其风险规避程度小于某个阀值时,整个供应链的期望效用是递减的,反之,当其风险规避程度超过某个阀值时,整个供应链的期望效用是递增的。性质4则说明在集中决策下,当线下渠道和线上渠道的市场份额相等时,整个供应链的期望效用是最低的。
3.2 分散决策模式
分散决策模式下,制造商和零售商的决策都以自身利润最大化为目标。由于假设零售商是供应链的领导者,制造商是跟随者,所以制造商和零售商之间进行博弈属于Stackelberg主从博弈。零售商和制造商的博弈分为两步:
第1步作为领导者的零售商,先确定其批发价溢价部分Δwr和Δwe,以使自己利益最大化。
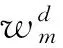
根据假设条件可知,在分散决策下,制造商和零售商的期望利润分别为
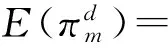
(9)
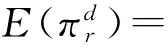
(10)
制造商和零售商的利润方差分别为
(11)
(12)
根据均值-方差理论,制造商和零售商的决策目标期望效用函数分别为

(13)
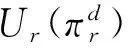
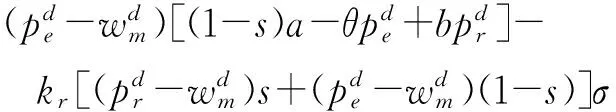
(14)
命题3分散决策模式下零售商双渠道最优价格和制造商最优批发价格为
(15)
(16)
(17)
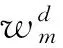
(18)
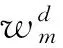
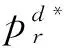
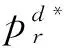
性质5说明在分散决策模式下,零售商的风险规避程度不仅影响线下和线上渠道的价格,也影响到制造商的批发价格。随着零售商对市场风险厌恶程度的增加,零售商会减少订货批量,并将降低线下和线上渠道的商品销售价格,以减少自己的损失。同时,制造商在零售商订货批量减少的情况下,将会提高商品的批发价格,实现自己利润最大化。性质6则说明顾客渠道偏好对双渠道价格的影响,即当大多数顾客偏好线下渠道时,零售商将会提高线下渠道的商品销售价格,并降低线上渠道价格,使自己利润最大化;同理,当大多数顾客偏好线上渠道时,零售商将会提高线上渠道的价格,并降低线下渠道价格。
命题4分散决策模式下零售商、制造商和整个供应链的最大期望效用分别为

(19)
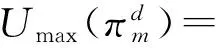
(20)

(21)
性质7在分散决策模式下,整个供应链的期望效用与零售商的风险规避kr关系如下:
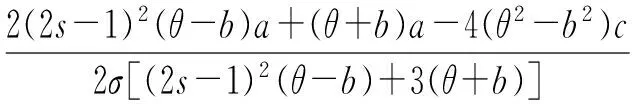
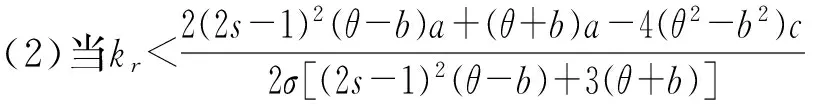
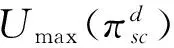
4 两种决策模式比较分析
4.1 两种决策模式下价格比较
(1)同一决策模式下的价格比较
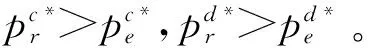
从上式易知:在同一决策模式下,当线下渠道市场份额大于线上渠道市场份额,且零售商的风险厌恶程度小于某一数值时,线下渠道价格高于线上渠道价格;当线下渠道市场份额小于线上渠道市场份额,且零售商的风险厌恶程度大于某一数值时,线下渠道价格低于线上渠道价格;当线下渠道市场份额等于线上渠道市场份额,且零售商的风险厌恶程度等于某一数值时,线下渠道价格等于线上渠道价格。
(2)不同决策模式下的价格比较
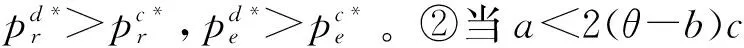
从上式易知:当市场基本需求量大于某一数值时,分散决策模式下的双渠道价格分别高于集中决策模式下相应渠道的价格;当市场基本需求量小于某一数值时,分散决策模式下的双渠道价格分别低于集中决策模式下相应渠道的价格;当市场基本需求量等于某一数值时,分散决策模式下的双渠道价格分别等于集中决策模式下相应渠道的价格。
4.2 两种决策模式下期望效用比较
根据上式分析可知:
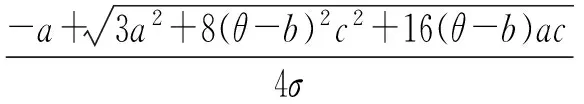
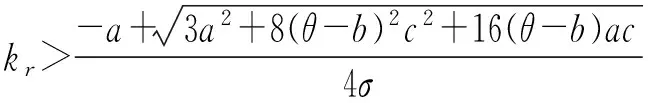
上式说明零售商的风险厌恶程度对供应链的期望效用有影响。当零售商的风险厌恶程度在某个区间取值时,集中决策时的整个供应链的期望效用大于分散决策时的期望效用;而当零售商的风险厌恶程度超过某个阀值时,集中决策时的整个供应链的期望效用小于分散决策时的期望效用。这个结论与在供应链参与方是风险中性时得到的结论是不同的。
5 算例分析
由于在模型中参数较多,表达式也较为复杂,为更直观地分析零售商风险厌恶程度对制造商、零售商的最优价格决策和对整个供应链的期望效用的影响,以及市场需求波动程度、线下渠道的市场份额、市场基本需求量、价格弹性系数、交叉价格弹性系数对制造商、零售商的最优价格、期望效用的影响,故借助数值算例来进行分析。
5.1 价格敏感性分析
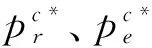
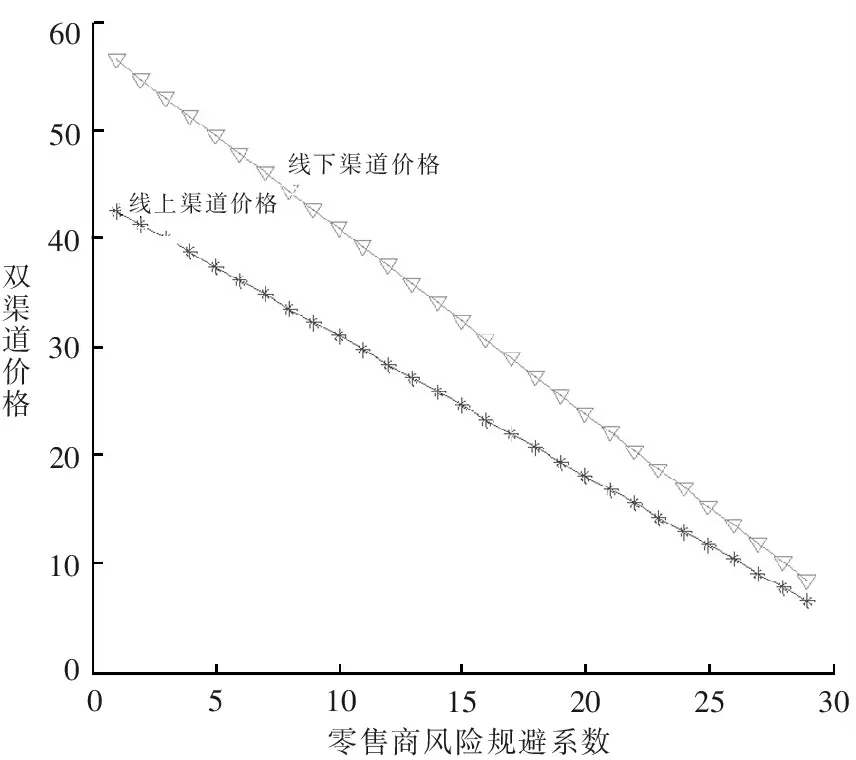
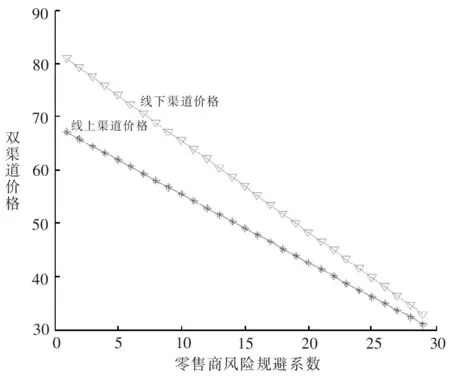
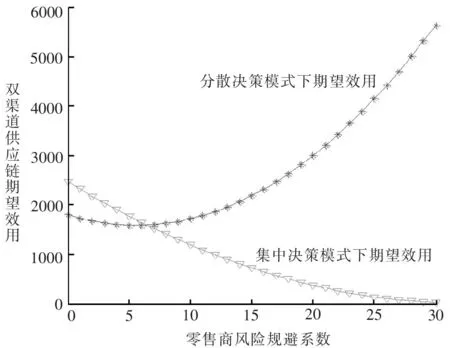
5.2 期望效用敏感性分析
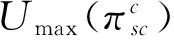

6 结论与启示
在一个制造商和一个零售商组成的线下和线上的双渠道供应链中,考虑到零售商是风险厌恶型的情况,从集中决策和分散决策两种模式分别建立了均值-方差模型,然后对两种决策模式下的零售商双渠道最优价格和整个供应链的最大期望效用进行对比,研究结果表明:
(1)零售商双渠道价格随着零售商风险规避系数和市场需求波动标准差的增加而降低,而制造商批发价格变化与此相反。
(2)当市场基本需求量大于某一数值时,分散决策模式下的双渠道价格分别高于集中决策模式下相应渠道的价格,反之亦然。
(3)当零售商的风险厌恶程度在某个区间取值时,集中决策时的整个供应链的期望效用大于分散决策时的期望效用,反之亦然。
(4)线上渠道和线下渠道价格随着价格弹性系数值的增加而减少,但随着交叉价格弹性系数值的增加而增加。
(5)线下渠道价格随着线下市场份额的增加而增加,线上渠道价格的变化刚好相反。
本文研究对管理上的启示在于:相对于供应链参与者的风险中性而言,供应链参与者的风险规避程度对零售商双渠道供应链的价格和期望效用都有不利影响。因此,供应链参与方对不确定的市场需求,应该利用历史数据和科学预测方法提高市场需求预测的精度,尽量减少需求不确定性所引起的风险和损失。
本文主要针对单个制造商和单个零售商的二级供应链进行研究,但现实中的供应链网络结构往往比较复杂,一般涉及多个制造商和多个零售商,它们之间的关系更加复杂,虽然这类问题比较复杂,但也是今后值得研究的方向之一。
[1] Brynjolfsson E, Michael D S. Frictionless commerce? A comparison of internet and conventional retailers[J]. Management Science, 2000, 46(4): 563-585.
[2] Chiang W K, Chhajed D, Hess J D. Direct marketing, indirect profits: a strategic analysis of dual-channel supply-chain design[J]. Management Science, 2003, 49(1): 1-20.
[3] Hsieh C C, Chang Y L, Wu C H. Competitive pricing and ordering decisions in a multiple-channel supply chain[J]. International Journal of Production Economics, 2014, 154(4): 156-165.
[4] Panda S, Modak N M, Sana S S, et al.. Pricing and replenishment policies in dual-channel supply chain under continuous unit cost decrease[J]. Applied Mathematics and Computation, 2015, 256(1): 913-929.
[5] Yao D, Liu J J. Competitive pricing of mixed retail and e-tail distribution channels[J]. Omega, 2005, 33(3): 235-247.
[6] Khouja M, Park S, Cai G G. Channel selection and pricing in the presence of retail-captive consumers[J]. International Journal of Production Economics, 2010, 125(1): 84-95.
[7] Wang X, Liu L. Coordination in a retailer-led supply chain through option contract[J]. International Journal of Production Economics, 2007, 110(1): 115-127.
[8] Pan K, Lai K K, Liang L, et al.. Two-period pricing and ordering policy for the dominant retailer in a two-echelon supply chain with demand uncertainty[J]. Omega, 2009, 37(4): 919-929.
[9] Huang W, Swaminathan J M. Introduction of a second channel: implications for pricing and profits[J]. European Journal of Operational Research, 2009, 194(1): 258-279.
[10] Zhang R, Liu B, Wang W. Pricing decisions in a dual channels system with different power structures[J]. Economic Modelling, 2012, 29(2): 523-533.
[11] Wang J, Wang A, Wang Y. Markup pricing strategies between a dominant retailer and competitive manufacturers[J]. Computers & Industrial Engineering, 2013, 64(1): 235-246.
[12] Zhang L, Wang J. Coordination of the traditional and the online channels for a short-life-cycle product[J]. European Journal of Operational Research, 2017, 258(2): 639- 651.
[13] Xiao T, Yang D. Price and service competition of supply chains with risk-averse retailers under demand uncertainty[J]. International Journal of Production Economics, 2008, 114(1): 187-200.
[14] Xie G, Yue W, Wang S, et al.. Quality investment and price decision in a risk-averse supply chain[J]. European Journal of Operational Research, 2011, 214(2): 403- 410.
[15] Xu G, Dan B, Zhang X, et al.. Coordinating a dual-channel supply chain with risk-averse under a two-way revenue sharing contract[J]. International Journal of Production Economics, 2014, 147(1): 171-179.
[16] Liu M, Cao E, Salifou C K. Pricing strategies of a dual-channel supply chain with risk aversion[J]. Transportation Research Part E: Logistics and Transportation Review, 2016, 90: 108-120.
[17] Kim K, Park K S. Transferring and sharing exchange-rate risk in a risk-averse supply chain of a multinational firm[J]. European Journal of Operational Research, 2014, 237(2): 634- 648.
[18] Li B, Hou P W, Chen P, et al.. Pricing strategy and coordination in a dual channel supply chain with a risk-averse retailer[J]. International Journal of Production Economics, 2016, 178: 154-168.
[19] Choi S. Risk-averse newsvendor models[D]. New Jersey: Newark Rutgers, 2009.
