聚焦数学课堂 落实数学核心素养的培养
——以《函数的单调性》的教学为例
2018-01-29林晴岚陈柳娟
林晴岚 张 洁 黄 勇 陈柳娟
(福建教育学院数学研修部,福建 福州 350025)
一、从教学整体结构把握课程,落实培养学生的数学核心素养
数学核心素养的培养是一个全方位多角度的培养工程。数学课堂是培养数学核心素养的主阵地。教师应从学科价值、社会价值、育人价值三方面站在课程的高度理解教材、解读教材、用好教材。在此基础上,利用课堂的教与学促进学生对数学基础知识的产生、发展、合理应用有思维体验经历过程积累,形成数学学习的基本思维经验,增加解决数学问题的基本能力,进而实现通过数学课程的学习培养扎实数学基础知识、提升数学解决基本问题能力,形成数学解决问题基本思想、基本方法,促进学生形成以数学的眼光看世界,以数学的思维思考世界,以数学的语言表达世界的数学素养。
1.教材分析与处理、学情分析
函数是数学中最重要的基础概念之一,函数作为中学数学教学的主体内容,几乎每一章都贯穿着函数的思想,可以说函数的思想是整个高中数学的“纲”,是基础数学语言。函数的教学分为三个阶段:第一阶段在九年义务教育的第三学段(即初中)数学课程中,以学习一次函数、正比例函数、反比例函数、二次函数内容为主,探讨函数的概念、表示法、图像画法为主;第二阶段在高中数学必修课程中,以学习指数函数、对数函数、幂函数、三角函数、数列为主,从中获得较系统的函数知识,培养函数应用意识;第三阶段在高中数学选修课程中,以学习函数导数为主,培养应用导数知识解决具体问题的能力。
《函数的单调性》这节课是高中数学必修1第二章《函数》第三节中的学习内容,是学生在初中数学学习过程中初步了解函数的意义,从变化的观点理解函数概念、性质,形成对简单的基本初等函数的感性认识的基础上,用对应的观点更深入理解函数概念,学习研究函数的单调性。
二、在“教”与“学”的过程中发展学生的数学核心素养
函数这章的学习是培养学生从具体的函数中观察、梳理变化的共性特征,从而抽象出一般函数所具备的性质,并能从图形的直观形象状态,通过合理的变式、引申,引导学生学会归纳数学方法,能用严谨的数学推理,抽象数学问题的本质,最终落实到能用数学抽象的符号语言正确表述变化特征,从而促进数学思维的深度发展,提升学生的直观想象、数学抽象、逻辑推理与数学运算等数学核心素养。
1.创设问题情境,引入课题
问题1:观察第一组函数图像,指出其变化趋势?
从左至右函数图像呈现出 的变化趋势,教师通过“引”学生观察函数图像,能用形的直观语言说出随着函数从左至右的变化特征是图像具有上升变化趋势。

“导”出用数学语言表述函数单调递增的特征:函数图像在该区间内逐渐 “上升”,用数学的语言表达为:当x的值增大时,函数值y也随着x增大而增大。
【设计意图】通过从具体函数的图像观察,让学生形成对函数的单调性的图形特征的感性认知到数学抽象概念形成体验,培养学生的直观想象素养。学生用数学语言描述单调递增函数的定义形成的抽象概括过程,培养学生的数学抽象和逻辑推理素养。
问题 2:如果存在 x1<x2<…<xn<…无数个取值,均满足有 f(x1)<f(x2)<…<f(xn)<…成立,能否判断函数在定义域R上是增函数吗?
从具体的实例出发对问题进行分析,进而抽象概括出单调增函数的概念:设函数y=f(x)的定义域为I,如果对于属于定义域I内某个区间D上的任意两个自变量的值 x1,x2,当 x1<x2时,都有 f(x1)<f(x2),那么,就称函数y=f(x)在区间D上是单调递增,区间D也称函数的单调增区间。
【设计意图】教师引导学生由特殊到一般,分析、比较、归纳、抽象、概括,通过从具体函数的取有限点到无限点,以及对无限点与任意点的探究,引入一般函数的单调性的数学符号语言定义,掌握关键词:定义域、子区间、任意、都有、单调、增区间。让学生感受从具体函数逐渐过渡到抽象函数的研究过程。使学生体会函数单调性用数学语言严谨描述单调递增函数的定义形成过程,培养学生的直观想象、数学抽象和逻辑推理素养。
2.类比探究,形成概念
问题3:观察第二组函数图像,指出其变化趋势?
从左至右函数图像呈现出______ 变化趋势。
在学生回答上述图像趋势后,“引导”学生用数学语言表述函数单调递减的特征:函数图像在该区间内逐渐“下降”。用数学语言表达为:当x的值增大时,函数值y也随着x增大而减少。
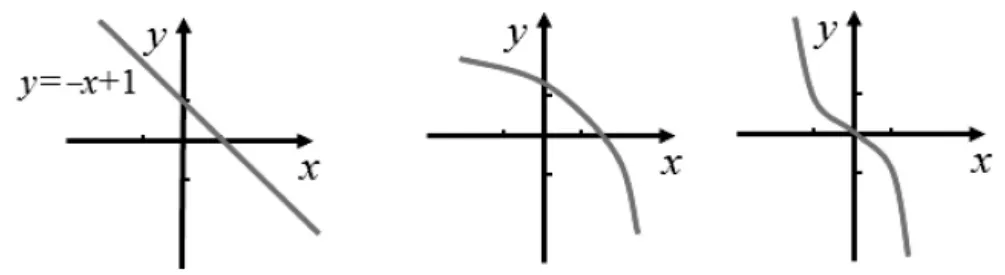
问题4:请用类比单调增函数的数学符号语言定义给单调减函数下一个定义?
【设计意图】通过对比函数单调递增、递减的图像,让学生形成对函数的单调性的几何直观图形特征认知,引导学生类比得到单调减函数的定义,感受函数递增、递减两者在定义上的不同关键点。使学生从对初中特殊函数直观图形的研究逐渐过渡到对一般函数单调性的抽象定义研究中,培养学生的直观想象、数学抽象和逻辑推理素养。
整合单调递增、单调减概念,函数单调性统一表达为:设函数y=f(x)的定义域为I,如果对于属于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有 f(x1)<f(x2)或 f(x1)>f(x2),那么,就称函数y=f(x)在区间D上是单调增或减函数,区间D也称函数的单调增或减区间。
【设计意图】通过对具体函数单调性的符号语言的研究,揭示其数学本质,让学生经历函数的单调性从用“图形语言”“文字语言”过渡到用“符号语言”描述的过程,实现对函数单调性的三种数学语言的表达形式的认知,从而提升学生的抽象与概括能力。培养学生的直观想象、数学抽象和逻辑推理素养。
3.通过典型例练,促进理解单调性概念
例 1 如图是定义在[-5,5]上的函数 y=f(x)的图像,根据图像说出y=f(x)的单调减区间是?
学生出现的错误为:y=f(x)的单调减区间是[-5,-2]∪[1,3]。
教师对错误答案进行分析后,进一步提问:能不能说函数 f(x)=在定义域(-∞,0)∪(0,+∞)上是单调减函数?
【设计意图】让学生利用具体的函数图像,学习用正确数学符号语言表达函数单调区间,加深对函数单调性理解。培养学生的直观想象、数学抽象、数学运算和逻辑推理素养。例 2 证明:函数 f(x)=x-在(0,+∞)上是增函数。
证明:设 x1,x2是区间(0,+∞)上的两个任意的实数,且 x1<x2……设值。

【设计意图】规范训练学生运用严谨的数学符号语言证明函数的单调性,培养学生的逻辑推理和数学运算素养。让学生进一步理解函数的单调性的抽象概念,培养学生的数学抽象素养。让学生体会函数的单调性与函数图像之间联系与转化,培养学生的直观想象素养。
【巩固练习】练习 1:设函数 y=f(x)的定义域为 I,如果对于属于定义域I内某个区间D上的任意两个自变量的值 x1,x2,当 x1<x2时,都有 f(x1)< f(x2),那么,就称函数y=f(x)在区间D上图像是否一定是上升的?如果是,请给说明;不是,请举出反例。
【设计意图】让学生从另一个角度理解函数的单调性,领悟数学关键词“任意”“都有”“增函数”“减函数”在数学符号与概念中的重要作用,揭示函数单调性定义既是判定又是性质。培养学生数学抽象和逻辑推理素养。

【设计意图】让学生掌握运用定义法规范证明函数单调性的表达方式,提升学生的代数运算能力、数学交流能力。培养学生的数学运算和逻辑推理素养。在教学过程中,教师通过引导学生亲身经历数学概念从具体到抽象、从特殊到一般,从有限到无限的符号化过程,让学生在解决问题的过程中实践体会的基础上,从不同角度观察同一事物共同属性,以抽象为基础、通过实践尝试、循序渐进地引导学生经历由感性认识到抽象概括出数学严谨概念形成重要过程,发展了学生的数学核心素养。
三、在评价中提升学生的数学核心素养
数学的独特育人功能主要体现在培养学生的思维特别是逻辑思维上。其主要目的是使学生学会思考,特别是学会有逻辑地思考、创造性思考。函数单调性的教学能以学生的原有认知结构为基础,重视让学生通过对已有知识的再认识研究发现其变化规律,从图形的观察得出直观自然语言表达,培养学生的直观想象素养,逐步引导过渡到会用数学的抽象符号语言表达,培养学生的数学抽象素养;掌握用类比的方式学习新知、认识新知、理解新知、应用新知,培养学生的逻辑推理素养。
在整个课堂教学的过程中,教师给学生较充分的思考时间,从传授转变为引导,让学生经历对问题的思考、变通、迁移过程,积累基本数学活动经验。整个课堂落实函数单调性学习的知识量、数学学习的活动量、问题的思维量,学习形式也从单一转变为多元,从中培养了学生的数学探究能力、知识应用能力、提问能力、交流与合作能力、反思能力,实现了数学学习化神奇为平常,化复杂为简单的目标。
[1]林晴岚,陈柳娟,张洁.探寻高考数学试题之源,找准复习目标回归教材——以函数导数应用专题为例[J].中国数学教育,2017(5).
[2]叶亚美.感受·体验·感悟[J].数学教学通讯:中教版,2006(2).
[3]陆斌.是教教材还是用教材教——从一节函数单调性的说课谈起[J].数学教学,2009(4).
