利用风阻温升估算气封间隙和流量
2018-01-29熊元建蔡国煌周洪宇赵仕志
熊元建, 周 娜, 蔡国煌, 周洪宇, 艾 松, 赵仕志
(东方汽轮机有限公司,四川德阳 618000)
符号说明:
cp——比定压热容,J/(kg·K-1)
T——温度,K
p——压力,Pa
υ——比体积,m3/kg
μ——黏度,N·s/m2
μJ——绝热节流系数,K/Pa
Cms——气封力矩系数
Cw——流量系数
Cf——摩擦因数
CfR——转子表面摩擦因数
CfS——静子表面摩擦因数
Cd——气体压缩因子
A——面积,m2
c——气封间隙,m
w——气封齿宽度,m
l——气封齿节距,m
h——气封齿高度,m
n——气封齿数量
r——半径,m
X——气封转子表面长度,m
τ——壁面剪切应力,Pa
H——风阻耗功,kW
N——转速,r/min
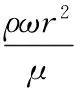
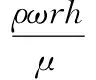
ω——旋转角速度,rad/s
ρ——密度,kg/m3
R——气体常数,J/(kg·K),空气为287.06 J/(kg·K),水蒸气为461.9 J/(kg·K)
Prf——Egli公式压缩因子
qm——质量流量,kg/s
M——风阻力矩,N·m
β——旋转比
vcore——气流周向速度
Δ——计算差值
下标
in——进口
out——出口
篦齿气封是蒸汽轮机、燃气轮机等大型旋转机械中用于密封高压气体的重要部件.气封结构常工作在高温高压环境中,水蒸气、空气等流动介质的温度变化会影响金属壁面温度场分布,温度场分布不均会给结构设计、强度校核工作带来困难,因此在工程应用中开展篦齿气封的介质温度变化研究具有非常重要的意义.
水蒸气、空气等流动介质流过高速旋转的篦齿气封时,气封齿和气封体壁面与流体介质之间的黏滞力做功产生热量,热量被流体介质吸收后,介质焓值升高,温度也会升高.针对高速旋转气封的介质温度变化,航空发动机方面的专家对以空气为介质的气封流动过程进行了大量试验和理论计算分析.Millward等[1]、Mcgreeham等[2]试验了多种气封结构在不同转速、间隙时的风阻温升情况,推荐了计算风阻温升的半经验公式.国内相关部门也总结了适用的经验公式[3].晏鑫等[4-5]采用数值仿真方法对高速旋转光滑面篦齿气封内的流动和传热特性进行了研究.从已有的文献来看,对航空发动机的篦齿封严风阻温升预测已有十分成熟可靠的方法,但对于采用水蒸气为介质的高速旋转篦齿气封风阻温升的研究,还鲜有报道.
介质温度变化与介质流量有关,而介质流量又受气封间隙制约.曹玉璋等[6]采用逐步近似计算方法来计算气封实际工作间隙和气封流量,但该办法迭代流程繁琐,且迭代过程比较理想化,在工程应用中有较大难度.在复杂旋转机械中,直接测量篦齿气封流量通常难以实现,可通过测量其他相关参数来估算气封流量.
对于某种气封结构,介质温度变化可表达为多个参量的函数:
ΔT=f(qm,r,N,Z)
(1)
其中,Z为表征气封结构尺寸的参数,如l、w和h.
qm=g(p,T,r,c,n)
(2)
根据式(1)和式(2)建立介质温度变化ΔT与气封间隙c之间的关系,若能获得工作气封的介质温度变化,便可求得气封实际工作间隙和介质流量.
笔者分别采用理想气体空气和水蒸气2种介质,综合运用半经验公式和数值仿真方法计算篦齿气封在转速N=0和N=3 000 r/min时的介质温度变化.由于介质通过气封齿的过程是节流过程,空气和水蒸气的最大转回温度较高,经节流后温度可能会降低,需要评估空气和水蒸气在气封中的节流温降程度,以修正节流温降对风阻温升的影响.据此,笔者提出了根据流体风阻温升直接估算气封实际工作间隙和泄漏流量的方法.
1 计算模型
所研究的计算模型采用某旋转机械交错式篦齿气封.图1为其结构尺寸示意图.

图1 交错式篦齿气封结构尺寸
气封三维模型网格结构图如图2所示.网格划分采用商业软件Ansys Workbench平台.计算模型取1/72整机模型作为研究对象,采用扫掠网格,分别采用最小网格0.1 mm、0.144 mm、0.2 mm、0.25 mm和0.3 mm进行网格无关性验证,并以各算例收敛后的出口流量变化作为网格无关性的判断标准.根据计算结果(见图3),模型最小网格为0.1 mm时,流量几乎不再随网格大小而变化.为节省计算资源和时间,最终模型采用最小网格为0.1 mm,对应网格节点数量为70.8万,单元数为68.0万.计算采用CFX流体动力学软件.
为研究水蒸气和空气2种不同介质在不同转速下的总温升情况,共选用4个流体动力学(CFD)算例(见表1).空气工质为理想气体;水蒸气选择材质库中的steam5,为干蒸汽,符合IAPWS-IF97标准,其工作范围:450 K≤T≤900 K,1 000 kPa≤p≤30 000 kPa.
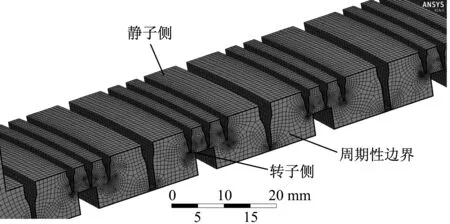
图2 气封三维模型网格结构
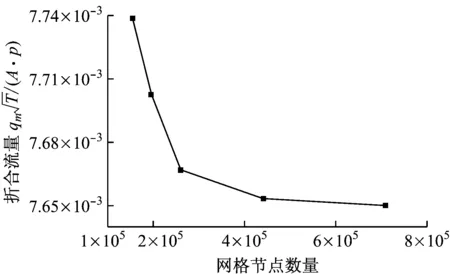
图3 网格无关性验证
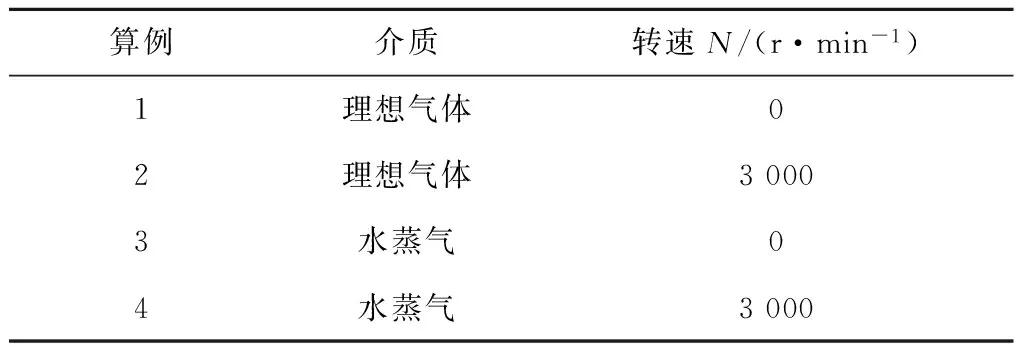
算例介质转速N/(r·min-1)1理想气体02理想气体30003水蒸气04水蒸气3000
由于空气、水蒸气的最大转回温度较高,需要评估流体通过气封齿后节流温降的影响.根据节流微分效应和理想气体克拉伯龙方程:
(3)
pυ=RT
(4)
理想气体在N=0时的节流温升将恒等于0.
在用CFX软件计算流动过程中,湍流模型采用切应力输运模型(Shear Stress Transport),计算域紊流度设置为5%.壁面采用无滑移绝热壁面,不考虑工质与壁面的换热过程.
气封进口总压pin,t=3 200 kPa,出口背压pout,s=2 780 kPa,进口总温Tin,t=805 K.
2 计算结果
精确的传热分析需要具有合理的网格Y+值.图4为各算例模型壁面Y+分布云图,其中算例2气封壁面Y+最大值为30.
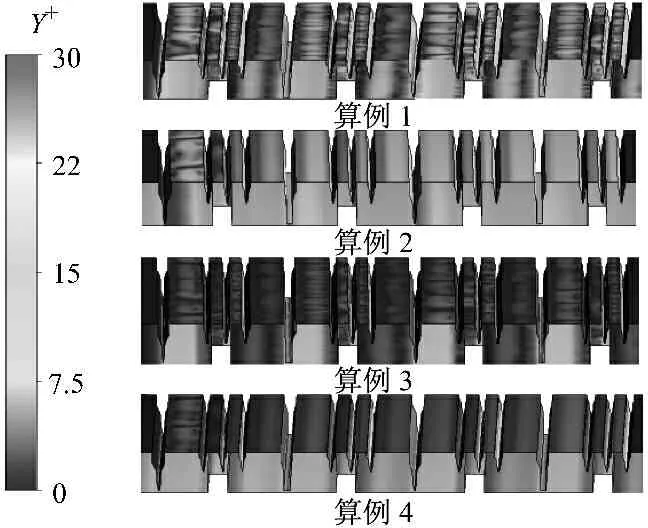
图4 气封壁面Y+分布云图
Fig.4 Seal wallY+value contour
在绝热工况下,气封壁面与流体介质之间的黏滞力做功,转子的能量损失转化为流体的内能,导致流体温度升高.图5给出了4种算例的气封子午面总温分布.





图5 气封子午面总温分布云图
从图5可以看出,算例1和算例3中,当转子转速N=0时,因转子不对流体介质做功,流体流经气封后总温变化不明显,算例3中水蒸气从进气侧到出气侧的总温略有降低.而算例2和算例4中,当转子转速N=3 000 r/min时,旋转转子对流体介质做功,使流体总温升高,且空气比水蒸气的温升更为明显.
为评估气封内流体介质的周向旋转量的大小,引入参数旋转比β,其定义式如下:
(5)
图6为旋转气封子午面旋转比分布云图.由图6可知,篦齿气封在转速N=3 000 r/min时,空气在气封齿中的旋转比约为0.2~0.4,子午面上其全局变化范围为0~0.89;水蒸气在气封齿中的旋转比约为0.2~0.35,其全局变化范围为0~0.94.


图6 气封子午面旋转比分布云图
3 经验公式计算
3.1 气封流量计算
为了验证CFD数值仿真计算,分别对空气和水蒸气介质在N=3 000 r/min时采用广为认可的Egli[1,7]公式计算气封流量,并采用多种经验公式计算风阻温升.经验公式不适用于计算转子转速为0的情况.
计算气封流量的Egli公式为:
(6)
(7)
其中,气体压缩因子Cd可根据气封间隙c和气封齿宽度w的比值进行取值,在图7中取Cd=0.68.
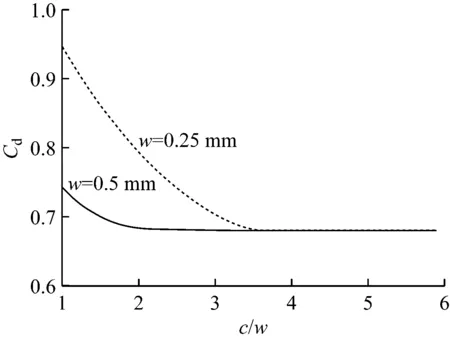
图7 Egli公式中气体压缩因子与c/w的关系图[1,7]
计算得到的空气和水蒸气的气封流量见表2.

表2 CFD和Egli公式计算所得气封流量、旋转比和Re
从表2可以看出,CFD计算气封流量与经验公式计算气封流量符合得较好.同时根据计算结果可以看出,旋转对气封流量的影响并不明显.
3.2 气封风阻温升计算
采用文献[1]~文献[3]中的经验公式计算流体介质流经气封后的风阻温升.3种经验公式均是基于气封壁面上的摩擦因数Cf来计算气封转子对流体介质的风阻耗功H的,但三者的摩擦因数Cf表述各有不同.Millward等[1]推荐计算气封力矩系数Cms,Mcgreeham等[2]推荐的计算公式需求取转子表面摩擦因数CfR和静子表面摩擦因数CfS,《航空发动机设计手册》[3]则推荐计算综合的摩擦因数Cf.具体表述如下.
Millward等[1]推荐的气封力矩系数为:
(8)
其中,旋转雷诺数Re的特征尺寸为气封齿所在位置的平均半径.而流量系数为:
(9)
则风阻耗功
H=Cmsπρω3r4X
(10)
Mcgreeham等[2]推荐基于风阻力矩面积积分的公式如下:
风阻力矩
(11)
壁面剪切应力
τ=Cf(0.5ρω2r2)
(12)
转子和静子表面摩擦因数
CfR=0.042(1-β)1.35Re*-0.2
(13)
CfS=0.063β1.87Re*-0.2
(14)
则风阻耗功
(15)
文献[2]中,转子表面摩擦因数CfR和静子表面摩擦因数CfS共同用于求取旋转比β.根据CFD计算结果,算例2和算例4的旋转比β平均值分别取为0.26和0.25(见表2).
根据定义,修正旋转雷诺数Re*的特征尺寸取为气封齿高度h.
《航空发动机设计手册》[3]推荐的计算风阻耗功公式如下:
式中:rt,i为第i齿齿顶半径,m;rb,i为第i齿齿根半径,m.
第i齿位置的旋转雷诺数为:
(17)
此处第i齿位置旋转雷诺数Rei的特征尺寸取为各气封齿所在位置的平均半径.由于在计算中难以逐级计算各级气封齿处的雷诺数,在实际计算时可仅计算气封齿进出口压力对应的平均雷诺数.
第i齿摩擦因数Cf,i表达式为:
(18)
经多次迭代逼近计算可得到Cf.
根据风阻耗功、介质流量和比定压热容可计算流体流经气封后的风阻温升:
(19)
CFD和3个经验公式计算的气封进出口风阻温升结果如表3所示.从表3可以看出,算例1中,空气在转速N=0时的温升为-0.035 K,可以忽略不计;算例2中,空气在转速N=3 000 r/min时,CFD计算所得气封进出口风阻温升与式(15)和式(16)计算得到的结果比较一致,但式(15)在使用时依赖于旋转比β的选取.
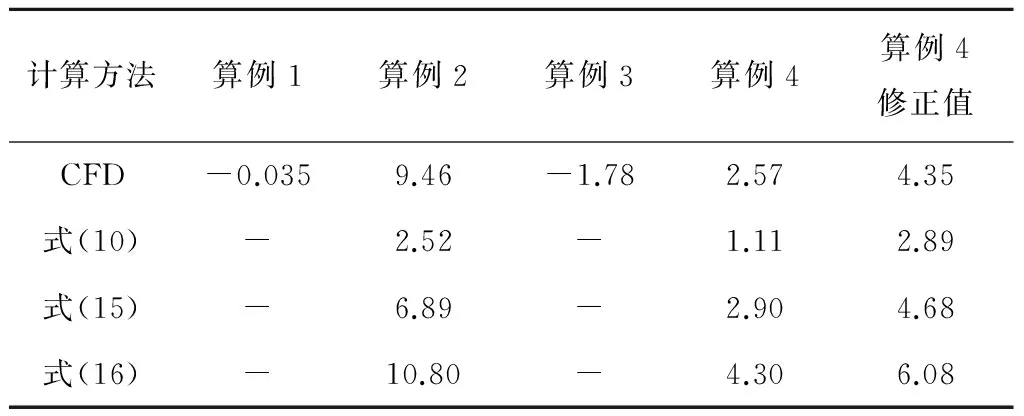
表3 CFD和经验公式计算所得气封进出口风阻温升
算例3中,水蒸气在转速N=0时的温升为-1.78 K,这是由于节流导致水蒸气(实际气体)有温降.算例4中,水蒸气在转速N=3 000 r/min时风阻温升仅为2.57 K,但水蒸气流过旋转气封时仍会有节流温降,节流温降由压力变化决定,而几乎与转速无关,故可对算例4进行-1.78 K的修正,得到不考虑节流温降时的风阻温升为4.35 K,与采用式(14)和式(15)计算的结果较为吻合.
对比3种经验公式的计算结果,Millward等[1]推荐公式计算的风阻温升结果偏小,Mcgreeham等[2]和《航空发动机设计手册》[3]推荐公式的计算结果与CFD计算结果符合得较好.
4 工程应用
根据上述数学模型,某种已知结构气封在给定进出口压力、温度和转速时,风阻耗功基本上不随其他参数变化,由此根据监控气封进出口温升来反求气封实际工作间隙和泄漏流量.气封设计间隙为c0时的风阻温升为ΔT0,联立式(6)和式(19),经归一化后可得:
(20)
式(20)对应图8的数学模型计算曲线.从图8可以看出,若实测气封风阻温升为ΔTi,便可求得气封工作间隙ci.若在原型机验证试验中测得气封实际工作间隙ct,对式(20)引入修正量Δc=ct-ci,可得试验修正曲线,建立起优化的间隙与温升关联模型,并根据流量计算公式得到优化后的泄漏流量.
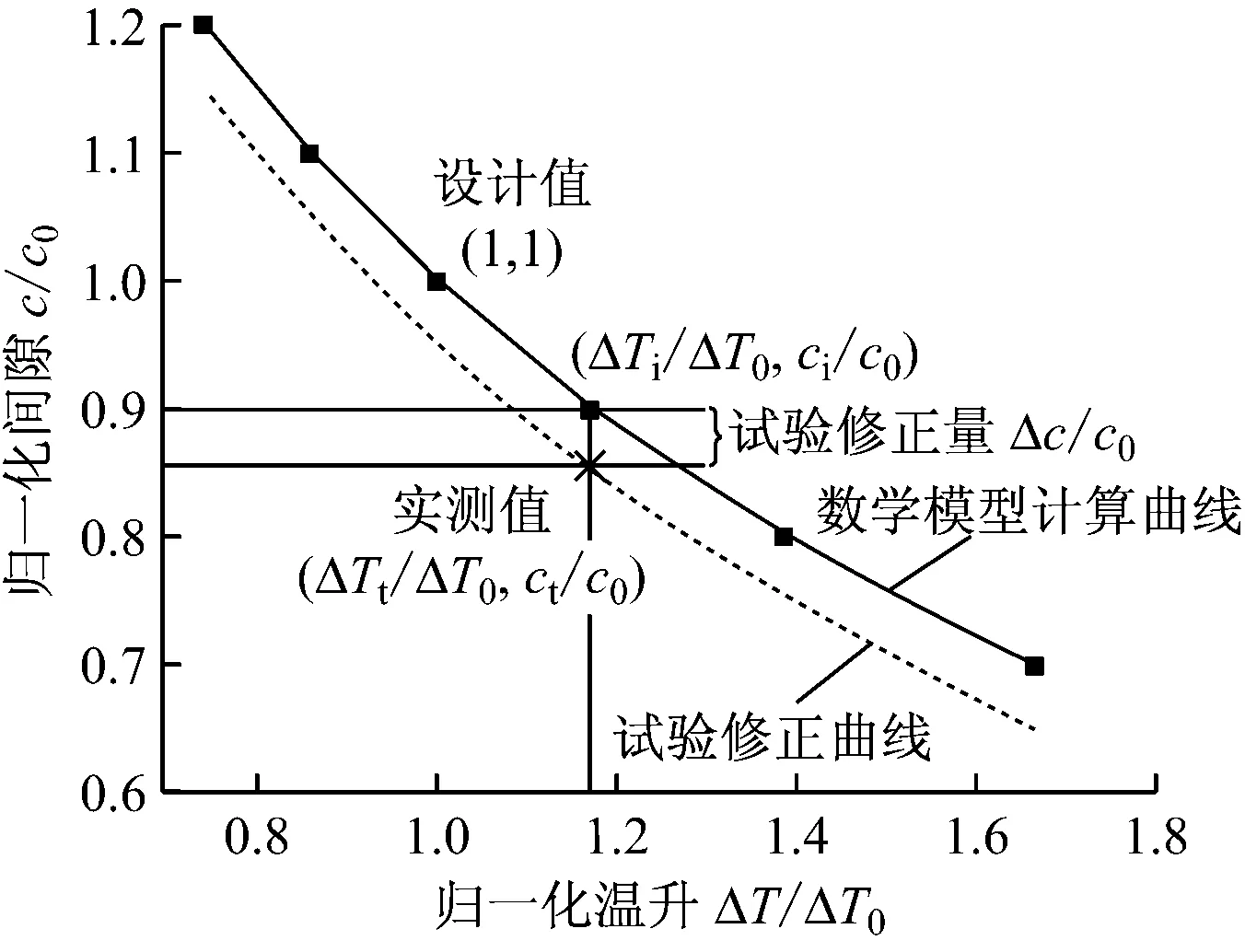
图8 归一化间隙随归一化温升的变化曲线
在原型机验证试验中需要花费高昂代价才能测得气封工作间隙.因此,气封结构定型后,在产品机或类似新设计机组上通过廉价手段监测风阻温升求得气封实际工作间隙,并得到泄漏流量,省去了迭代逼近法的繁琐过程,使计算结果不受气封变形等复杂因素的影响,具有重要的工程意义.
5 结 论
(1) 综合运用CFD数值仿真方法和多种经验公式,计算了空气和水蒸气2种不同介质在转速N=0和N=3 000 r/min时的温升特性.经验公式计算结果证明,在气封结构概念设计阶段,合理运用计算气封温升的经验公式具有较高的工程可靠性.
(2) 在相同进出口气体参数和转速条件下,空气风阻温升比水蒸气风阻温升更为明显,空气节流温降小,因此在燃气轮机等以空气为介质的旋转机械中,用温升特性估算气封工作间隙和泄漏流量的方法可行.水蒸气节流温降较明显,风阻温升一般较小,通过温升反推气封实际工作间隙会有较大误差.
(3) 根据空气在气封中的温升特性,提出根据监控气封进出口温升来反求气封实际工作间隙和泄漏流量的方法.根据原型机验证试验的实测温升和气封间隙修正数学模型,获得优化的计算模型来计算气封工作间隙和泄漏流量,在工程设计中具有重要意义.
[1] MILLWARD J A, EDWARDS M F. Windage heating of air passing through labyrinth seals[R]. The Hague, Netherlands: ASME, 1994.
[2] McGREEHAM W F, KO S H. Power dissipation in smooth and honeycomb labyrinth seals[R]. Toronto, Ontario, Canada: ASME, 1989.
[3] 《航空发动机设计手册》总编委会. 航空发动机设计手册第12册传动及润滑系统[M]. 北京: 航空工业出版社, 2002: 306.
[4] 晏鑫, 李军, 丰镇平. 高速旋转光滑面迷宫密封内流动和传热特性的研究[J].动力工程, 2008, 28(2): 190-194.
YAN Xin, LI Jun, FENG Zhenping. Investigations on the flow and heat transfer characteristics in high rotating smooth labyrinth seals[J].JournalofPowerEngineering, 2008, 28(2): 190-194.
[5] 晏鑫, 李军, 丰镇平.迷宫密封传热特性的数值研究[J].西安交通大学学报, 2012, 46(11): 1-5, 29.
YAN Xin, LI Jun, FENG Zhenping. Numerical investigations on heat transfer characteristics in labyrinth seals[J].JournalofXi'anJiaotongUniversity, 2012, 46(11): 1-5, 29.
[6] 曹玉璋, 陶智, 徐国强, 等.航空发动机传热学[M].北京:北京航空航天大学出版社, 2005: 62.
[7] EGLI A. The leakage of steam through labyrinth seal[J].TransactionofASME, 1935, 57(3): 115-122.
