基于自校正PID控制技术的余热发电系统设计

胡徐胜，刘 娟

（1.河海大学文天学院,安徽马鞍山243031;2.马鞍山职业技术学院 电气工程系，安徽马鞍山243031）

纯低温余热发电技术通过回收高能耗企业排放的温度低于300～400℃的中、低温的废蒸汽、烟气所含的低品位的热量来发电。余热发电温控系统具有惯性强、滞后时间长、非线性等特点，其温度一旦超调就无法用温控手段使其降温，因而很难用数学方法建立精确的模型和确定参数，应用传统的控制理论和方法也难以达到理想的控制效果。

1 纯低温余热发电极点配置自校正控制模型

余热发电的被控对象为AQC（Air Quenching Cooler篦式冷却机）锅炉的水量和温度。由阶跃响应的飞升曲线测得对象特性为具有纯滞后的一阶惯性环节，即：

其中，Kp=2.8；Tp=178s；τ=40s。

式子（1）带零保持器的广义对象脉冲传递函数为：

采样周期T的选择原则见文献[1].对大纯滞后对象，通常选择T=τ，则N=1，d=2.将实测被控对象参数代入式（1），得：

由此可得:b0=0.5636，a1=-0.7987

被控对象的模型为：

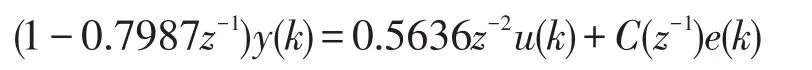
从极点配置的观点考虑，通常以典型的二阶系统闭环传递函数的形式：

作为目标。式（2）的特征方程对应的离散特征多项式为：

式（3）中，ωn为无阻尼自然振荡交频率，ξ为阻尼比。

对式（3），当二阶系统最佳阻尼比ξ=0.707时，在单位阶跃作用下的超调量σ=4.3%，相角稳定裕量 γ(ωc)=65.5°，它为二阶最佳动态响应模型。

采样周期T和ωn、ξ的关系，可以按照式（4）计算如下：

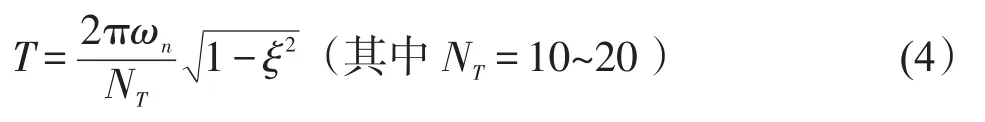
取NT=10。当ξ=0.707，T=40s时，得 ωn=0.022s-1.

式 （3） 的 期 望 特 征 多 项 式 为T(z-1)=1-0.7812z-1+0.2882z-2

为了避免在系统输出端参数突变而造成振荡，故选择：

在数字系统中，采用数字滤波器的PID算法,具体设计如下：

方程式上述 g0、g1、g2方程对Kp、TI和TD有唯一解，即：

为了将极点配置自校正控制器转换成增量型PID控制器，根据式（5）可选用如下形式：

根据增广型自校正闭环极点配置要求，闭环特征多项式应满足式（7），即:

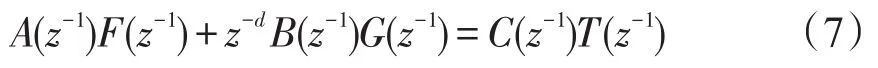
有下列等式成立：

令式（8）两边系数相等，解代数方程得：

将上述解代入式（6），得极点配置自校正PID控制器参数：

综上所述，极点配置自校正PID控制器极点配置成功。

2 系统仿真结果

图1为实时控制温度在设定值阶跃输入和扰动输入时的系统响应曲线。可以看出，对式（1）的被控对象，采用式（9）的PID参数，当温度设定值阶跃输入时，系统响应曲线接近二阶最佳，有超调量σ=5%（理论值是前文提到的σ=4.3%），调节时间较短，证实了极点配置方法设计PID控制器的正确性。

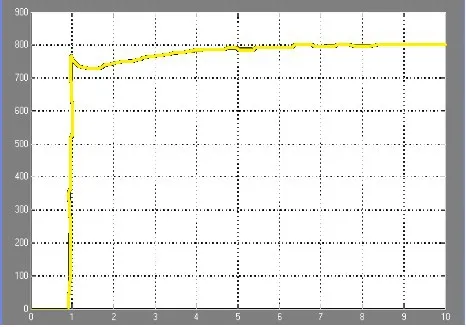
图1 仿真结果

3 结论

经过硬件调试和软件参数的设定与修改，采用该方法均能取得满意效果。经过调试运行，系统工作可靠稳定，操作方便；适当调整有关参数，可以达到较好的控制效果。实时仿真控制结果表明，基于自校正PID控制技术的余热发电系统设计，实现了对系统的控制，取得了令人满意的效果，这种控制方法鲁棒性强，对参数变化有较强的适应能力。

[1]刘伯春.离散系统采样周期的选择[J].化工自动化与仪表，1989（1）：28-33.

[2]刘金锟.先进PID控制及其MATLAB仿真[M].北京：电子工业出版社,2003.

[3]何鹏飞,吴雷.改进型模糊PID控制在光伏系统MPPT中的应用[J].江南大学学报（自然科学版）,2014,13（5）：546-550.

[4]王沫然.Simulink 4建模及动态仿真[M].北京：电子工业出版社,2002.

[5]裴洲奇.基于模糊算法的电阻炉温度控制系统的设计[D].大连:大连理工大学,2015

[6]晏亭太.智能自适应PID/PD控制器设计及仿真研究[D].哈尔滨:哈尔滨工业大学,2014.

[7]南新元，陈志军，等，基于模糊PID控制的电锅炉温度过程控制系统[J],自动化仪表,2008,29(5):5-8.

[8]滑娟，翟二宁，胡江峰,基于模糊PID算法的锅炉温度控制系统研究[J].中国机械,2014(11):201-202.

[9]范津齐.基于模糊自整定PID算法的电锅炉温度控制[D].沈阳：沈阳理工大学,2013.

[10]路桂明.基于模糊PID控制的电锅炉温度控制系统的研究[D].哈尔滨:哈尔滨理工大学,2007.

[11]吕晓峰.基于模糊PID理论的单片机智能温度控制系统设计[J].西部大开发刊,2011(5):56-56.

[12]张建民，王涛，王忠礼.智能控制原理及应用[M].北京：冶金工业出版社,2003.

[13]Zhou Hai-bo,Duan Ji-an,Zhou Zhen-yu.A simplified adaptive interval Type-2 fuzzy control in practical industrial application[J].中南大学学报（英文版）,2014(7),2693-2700.

[14]Han-Xiong Li,Shaocheng Tong.A Hybrid Adaptive Fuzzy Control for A Class of Nonlinear MIMO Systems[J].IEEE Transactions on Fuzzy Systems,2003(1).267-270

[15]Hao Ting.Deriving Analytical Input-Output Relationship for Fuzzy Controllers Using Arbitrary Input Fuzzy Sets and Zadeh Fuzzy AND Operator[J].IEEE Transactionson Fuzzy Systems,2006,5(5).257-262.

[16]Xinyu Du,Hao Ying.Derivation and Analysis of the Analytical Structures of the Interval Type-2 Fuzzy-PI and PD Controllers[J].IEEE Transactions on Fuzzy Systems,2010,4(4).356-361.