基于Kane动力学和通路矩阵的水下自重构机器人建模
2018-01-29王旭阳
徐 钻,杨 柯,葛 彤,王旭阳
(1.杭州电子科技大学 机械工程学院,杭州 310018;2.上海交通大学 船舶海洋与建筑工程学院,上海 200240)
0 引 言
水下自重构机器人由相同模块组成,可以根据环境和任务需要通过自重构策略动态重构出所需的构形。水下自重构机器人构形的变化增强了其在复杂多变的水下环境中的适应能力[1-2],但同时增加了建模的难度。与常规水下机器人AUV和ROV相比,水下自重构机器人的运动学和动力学显然要复杂很多[3-4]。
水下自重构机器人建模需解决两个问题:统一构形描述方法和建模方法。统一构形描述是指对水下自重构机器人模块间的运动关系进行描述。由于水下自重构机器人的构形是不断变化的,因此水下自重构机器人的统一构形描述是比较困难的。为了解决这一问题,引入了图论的相关知识。通过顶点和有向弧表征模块的杆件和关节,建立运动关系图,解决了水下自重构机器人的表示方法问题。通过可达矩阵和通路矩阵描述模块间的连接问题,这就解决了水下自重构机器人的统一构形描述问题。建模的方法比较多,主要包括 Newton-Euler方程[5-6]、Lagrange 方程[7]、Routh 方程、Appell方程[8]、Kane 方程[9-12]等。我们使用不同的方法对一个物体的同一种运动进行研究,最终得到的结果是相同的,但这些方法的计算速度和计算量是不同的。
Newton-Euler方程包含关节间的相互作用力,在推导机器人运动与力之间的关系时,相互作用力很难消除。因此,Newton-Euler方程主要用于设计阶段对施加到机器人上的力进行分析。而Lagrange方程、Routh方程和Appell方程通常为非线性微分方程,对这些方程进行求解时运算速度慢、耗费时间长。Kane方程在解决复杂系统的动力学问题时非常方便。Kane方程比较直观,因为它消除了Newton-Euler方程中存在的相互作用力和Lagrange方程需要的势能函数。Kane方程使用广义坐标,从而可以方便地施加约束。在Kane方法中使用广义速度,使得为非完整约束系统选择一组相互独立的运动变量成为可能,从而获得一阶微分形式的动力学方程。Kane方程提供了一个将外部作用力添加到机器人模型中的直观方法,并且Kane方程可以很容易地整理成非常适用于控制算法的闭环形式。最终的动力学模型可以为“哪些力真正影响动力学模型”提供物理解释。
本文主要是针对水下自重构机器人构形多变的特点,探讨了在动力学建模过程中存在的问题及解决方法,并提出了采用统一构形描述与Kane方程相结合的方法解决水下自重构机器人的动力学建模问题。
1 水动力计算
通常,作用在刚体上的水动力包括:浮力、拖曳力和拖曳力矩、附加质量力和附加质量矩[13]。水下自重构机器人是由相同模块组成(如图1所示,、s和表示与模块sk固结的相互垂直的单位矢量,满足右手法则),每个模块可以近似为长方体,因此,我们可以计算单个模块的水动力,将所有模块的水动力相加即可获得水下自重构机器人的水动力。
第k个模块sk受到的浮力为

式中:ρ表示流体的密度;Vsk表示模块sk排开流体的体积;g=[0 0 9.8 ]T为重力加速度;n为组成水下自重构机器人的模块数量。
模块s的拖曳力可以表示为[3-4]
k


图1 水下自重构机器人的组成模块Fig.1 The module of the underwater self-reconfigurable robot
模块sk的拖曳力矩可以表示为

作用在模块s上的附加质量力和附加质量矩为[3-4]
k


2 统一构形描述
水下自重构机器人可以根据任务需求和海洋环境信息动态重构出不同构形,因此,很难对水下自重构机器人的所有构形进行统一的描述。为了描述水下自重构机器人的所有构形,我们需要解决以下问题:对模块的设计要求、运动关系描述、可达矩阵和通路矩阵。
(1)对模块的设计要求。为了不失一般性,组成水下自重构机器人的模块应满足以下要求:①关节具有一个自由度;②杆件具有对称的几何特性;③杆件上具有多个连接端口。关节模块可以通过标准的接口连接到杆件上。对称的几何特性可以使模块具有灵活的装配模式。在这种情况下,多自由度的运动可以由多个1自由度的关节组合来完成。
(2)运动关系描述。在机构设计理论中,经常采用图论中的方法进行机构的运动关系描述,即用顶点和有向弧表示机构的杆件和关节[14]。使用这种图形表示方法,我们可以对连杆机构的基本结构进行分类,并运用图论中的理论对连杆机构进行枚举和分类。本文采用相同的符号表示水下自重构机器人的基本组成模块。图2给出了9模块8关节水下自重构机器人的构形图和运动关系描述。
(3)可达矩阵和通路矩阵。为了自动产生模块化机器人的动力学方程,我们引入了两个矩阵:可达矩阵和通路矩阵。运动关系图中两个顶点(杆件)间的连接可以通过可达矩阵来确定。通过该矩阵,我们可以获得模块化机器人从基准模块到其它任意模块的可达信息。
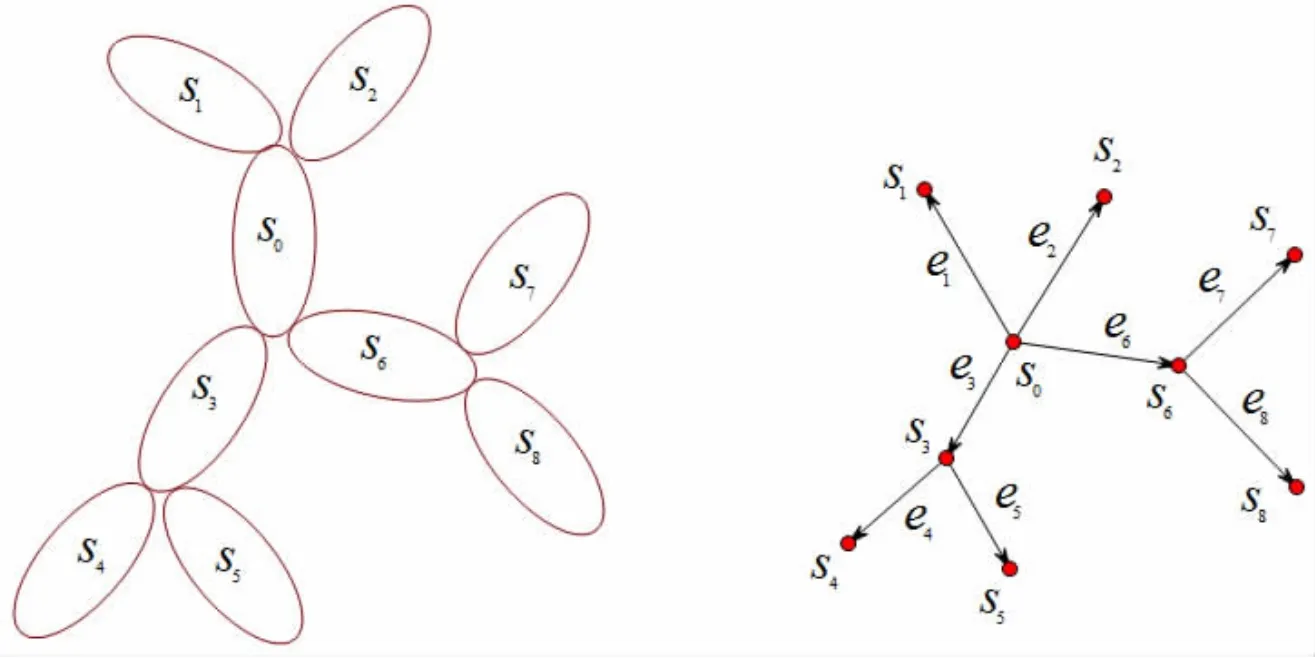
图2 水下自重构机器人构形和运动关系图Fig.2 Configuration and kinematic relation graph of the underwater self-reconfigurable robot
定义1可达矩阵(Accessibility matrix):用于描述n+1个模块组成的水下自重构机器人的运动关系的可达矩阵A是 (n+ 1 )×(n+ 1 )的矩阵,Aij(i,j=0,1,…,n )是可达矩阵的元素。 如果存在一条由si到 sj的有向路径,则 Aij=1;否则,Aij=0。
由于从si到si不存在有向路径,可达矩阵A的所有对角线元素为0。例如,图2所描述的水下自重构机器人构形的可达矩阵为:

从模块化机器人的可达矩阵A中,我们可以寻找到从基点到某一杆件的唯一路径,我们称之为通路。如果我们仅考虑由基点到最末端杆件的通路,水下自重构机器人构形的通路数量等于最末端杆件的数量。实际上,最末端杆件对应的是可达矩阵全为0的行。假设杆件si为最末端杆件,矩阵(A+I(n+1)×(n+1))T的第i+1行的所有非0元素表示的是从基点到si的通路上的杆件。找到所有的路径,我们可以获得下述矩阵:
定义2通路矩阵(Path matrix):用于描述n+1个杆件和m条通路组成的水下自重构机器人的运动关系的通路矩阵P是m×(n+ 1 )矩阵,Pij(i=1,2,…,m;j=0,1,…,n)是通路矩阵的组成元素。如果通路 i包含顶点 j,则 Pij=1;否则,Pij=0。
描述水下自重构机器人构形的运动关系所需的信息(例如,通路数量、通路中模块的连接序列、末端模块等)可以清晰地在它的通路矩阵中表示出来。例如,图2包含6条通路。6条通路可以表示为6×9的通路矩阵:

第一行表示水下自重构机器人构形包含模块s0和s1的分支;第二行表示水下自重构机器人构形包含s0和s2的分支;第三行表示水下自重构机器人构形包含模块s0、s3和s4的分支;第四行表示水下自重构机器人构形包含模块s0、s3和s5的分支;第五行表示水下自重构机器人构形包含模块s0、s6和s7的分支;第六行表示水下自重构机器人构形包含模块s0、s6和s8的分支。比较可达矩阵和通路矩阵,可以看出通路矩阵P的行对应的是A+I(n+1)×(n+1)中的第 2、3、5、6、8 和 9 列。
利用图论中的图形搜索技术和机构的运动关系描述,我们可以用统一的数学公式来描述水下自重构机器人的所有构形。
3 水下自重构机器人Kane动力学建模
3.1 运动学分析
水下自重构机器人的坐标系及矢径定义如图3所示,所有坐标系的坐标轴均满足右手法则。其中,sk表示水下自重构机器人的第k个组成模块;ck表示模块sk的质心;模块sk相对于模块 sj的转动角度为,模块 s0相对于惯性坐标系O的姿态角定义为和是与模块sk固结的相互垂直的单位矢量,载体坐标系的原点与sk的起点skO重合,且坐标轴的延长线过模块sk的质心 ck;表示惯性坐标系O的原点到模块sk的质心ck的矢径;表示惯性坐标系O的原点到模块si的起点siO的矢径。

图3 水下自重构机器人坐标系及矢径定义Fig.3 Coordinate system and radius vector of the underwater self-reconfigurable robot
为了计算模块sk相对于惯性坐标系O的姿态角,首先,需要确定模块sk位于第几条通路,即通路矩阵的第几行;其次,需要记录该行中从模块s0到模块sk的所有非零元素的编号。模块sk相对于惯性坐标系O的姿态角可以表示为
式中:i和 j取模块 s0到模块 sk的通路中的模块编号 (0≤i<k,i<j≤k );表示模块 sj相对于模块 si的转动角度;如果 si和 sj位于模块 s0到模块 sk的通路中,且si和 sj相邻,则 αij=1;否则,αij=0。同理,模块sk相对于惯性坐标系O的角加速度为

模块sk相对于惯性坐标系O的角加速度为

模块sk的质心相对于惯性坐标系O的矢径可写成:


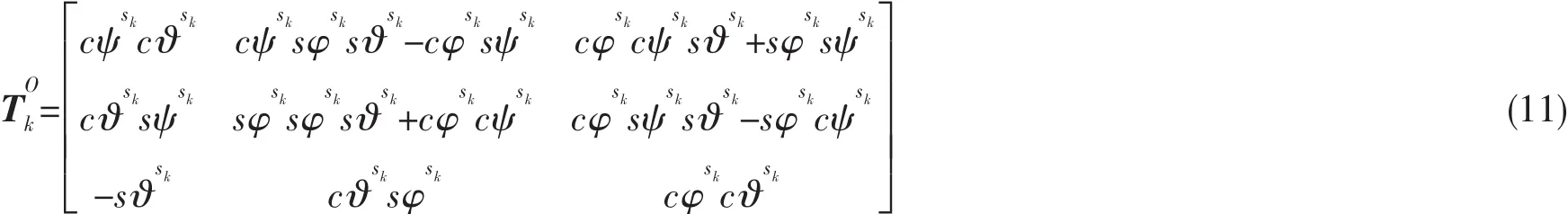

公式(9)可重写为

模块sk的质心相对于惯性坐标系O的速度可写成

模块sk的质心相对于惯性坐标系O的加速度可写成

偏速度和偏角速度为

3.2 动力学分析
模块sk的惯性力和惯性矩为

式中:mk为模块sk的质量;为模块sk的中心惯性张量。
模块sk的广义惯性力为

模块sk受到的重力Gsk对广义主动力的贡献为

作用在模块sk上的浮力Bsk对广义主动力的贡献为

作用在模块sk上的拖曳力和拖曳力矩对广义主动力的贡献为

作用在模块sk上的附加质量力和附加质量矩对广义主动力的贡献为

作用在模块sk上的控制力矩对广义主动力的贡献为


水下自重构机器人的广义主动力和广义惯性力可以表示为
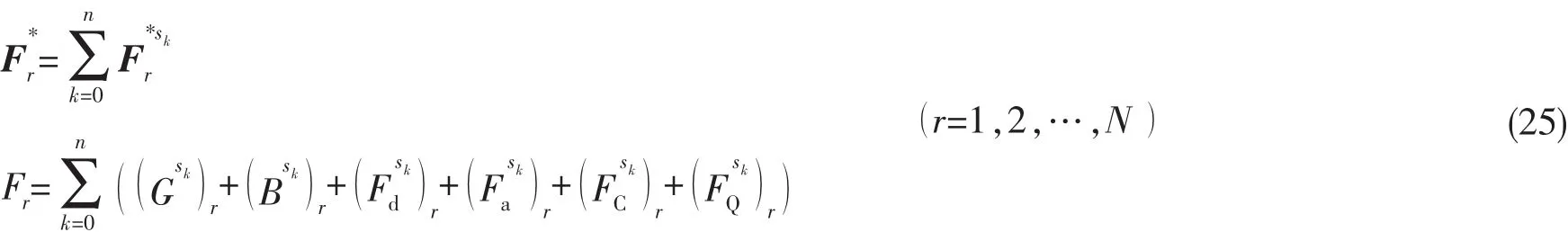
水下自重构机器人的Kane动力学方程为

4 建模实例
以水下自重构机器人的典型构形(水下四足行走构形,如图4所示)为例,采用本文提出的方法建立该构形的动力学模型。
水下四足行走构形的广义坐标定义为
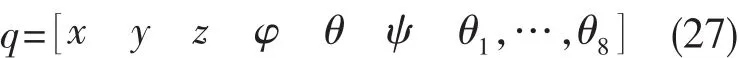
式中:x、y和z为身体质心在惯性坐标系下的坐标;φ、θ和ψ表示身体相对于惯性坐标系的欧拉角;θj(j=1,2,…,8 )表示关节角。
水下四足行走构形的广义速度为


图4 水下四足行走构形及其运动关系图Fig.4 Underwater quadruped walking configuration and its kinematic relation graph
由图 4 可知,水下四足行走构形共有四条通路,分别为:s0、s1、s2和 s3;s0、s1、s4和 s5;s0、s6和 s7;s0、s8和s9。因此,水下四足行走构形的通路矩阵为

考虑到s2、s4、s6和s8具有相似的运动学和动力学特征,我们将其归为一类,统称为大腿。同理,将s3、s5、s7和 s9归为一类,统称为小腿。 按照(16)~(24)式计算偏速度、偏角速度、广义惯性力和广义主动力,并按(25)式和(26)式写出最终的Kane动力学方程。
采用CPG设计水下四足行走构形的控制算法[15],将足与地面的接触问题等效为弹簧—阻尼模型,实现水下行走。图5给出了水下四足行走构形行走过程中,身体质心的运动轨迹。地面坐标z=0,竖直向下为正。x0表示前进方向的位移,z0表示竖直方向的位移,初始阶段(t=0)x0=0,z0=-1.2。由于行走过程中四肢交替运动,身体质心在竖直方向会产生震荡。
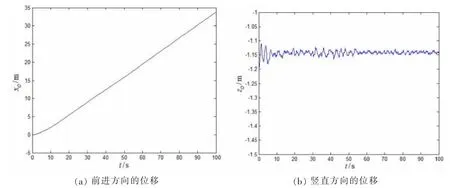
图5 身体质心的运动轨迹Fig.5 The trajectory of CM of body
5 结 论
本文系统地介绍了水下自重构机器人的统一构形描述方法;考虑到水下自重构机器人构形的复杂多变,提出了先对单个模块进行水动力计算,然后将所有模块的水动力相加来近似计算水下自重构机器人的水动力;给出了基于统一构形描述和Kane动力学的水下自重构机器人的通用动力学建模方法。以水下四足行走构形为例,验证了水下自重构机器人通用动力学建模方法的有效性。
[1]Xu Xusong,Ge Tong,Zhu Jimao.Optimal topological transformation of underwater modular self-reconfigurable robots[J].Robotica,2005,23:581-594.
[2]李家旺,葛 彤,吴 超,王旭阳.水下自重构机器人的自动对接控制[J].上海交通大学学报,2012,46(2):190-194.Li J W,Ge T,Wu C,W X Y.Docking control of underwater self-reconfigurable robot[J].Journal of Shanghai Jiaotong U-niversity,2012,46(2):190-194.
[3]Yang K,Wang X Y,Ge T,Wu C.Dynamic model of underwater snake-like robot using Kane’s method[J].Journal of Shanghai Jiaotong University,2014,19(2):146-154.
[4]Yang K,Wang X Y,Ge T,Wu C.A dynamic model of an underwater quadruped walking robot using Kane’s method[J].Journal of Shanghai Jiaotong University,2014,19(2):160-168.
[5]Maladen R D,Ding Y,Umbanhowar P B,et al.Undulatory swimming in sand:Experimental and simulation studies of a robotic sandfish[J].The International Journal of Robotics Research,2011,30(7):793-794.
[6]MA S G,Tadokoron.Analysis of creeping locomotion of a snake-like robot on a slope[J].Autonomous Robots,2006,20(1):15-23.
[7]Guo L,Liao Q Z,Wei S M.Dynamic modeling of bicycle robot and nonlinear control based on feedback linearization of MIMO systems[J].Journal of Beijing University of Post and Telecommunications,2007,30(1):80-84.
[8]Baruh H.Another look at the describing equations of dynamics[J].Journal of the Chinese Society of Mechanical Engineering,2000,21(1):15-23.
[9]夏 丹,陈维山,刘军考,等.基于Kane方法的仿鱼机器人波状游动的动力学建模[J].机械工程学报,2009,45(6):41-49.Xia D,Chen W S,Liu J K,et al.Dynamic modeling of a fishlike robot with undulatory motion based on Kane’s method[J].Journal of Mechanical Engineering,2009,45(6):41-49.
[10]李新友,陈五一,韩先国.基于Kane方程的SUPS/S并联机构动力学研究[J].机床与液压,2011,39(13):1-5.Li X Y,Chen W Y,Han X G.Dynamic analysis of a 3UPS/S parallel mechanism based on Kane equations[J].Machine Tool and Hydraulics,2011,39(13):1-5.
[11]沈 飞,曹志强,徐 德,等.基于Kane方法的机器海豚动力学建模及速度优化方法[J].自动化学报,2012,38(8):1247-1256.Shen F,Chao Z Q,Xu D,et al.A dynamic model of robotic dolphin based on Kane method and its speed optimization[J].Acta Automatica Sinica,2012,38(8):1247-1256.
[12]Cheng G,Shan X L.Dynamics analysis of a parallel hip joint simulator with four degree of freedoms(3R1T)[J].Nonlinear Dynamics,2012,70(4):2475-2486.
[13]Lin C C,Chen R C,Li T L.Experimental determination of the hydrodynamic coefficients of an underwater manipulator[J].Journal of Robotic System,1999,16(6):329-338.
[14]Muthyunjaya T S.Kinematic structure of mechanisms revisited[J].Mechanism and Machine Theory,2003,38(4):279-320.
[15]Yang K,Wang X Y*,Ge T,Wu C.Simulation platform of underwater quadruped walking robot based on motion genesis Kane 5.3 and central pattern generator[J].Journal of Harbin Institute of Technology,2014,21(3):24-29.
