桩土效应与地震对自升式平台动力响应影响分析

丁 军，官 腾，胡嘉骏，蒋彩霞，赵 南

（中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

自升式海洋平台结构复杂、体积庞大、造价昂贵，平台在服役期间所处的海洋环境十分复杂和恶劣，承受着多种随时间和空间变化的随机载荷，包括风、浪、流、冰和潮汐等，同时还受到海底地震的威胁。我国地处世界上两个最活跃的地震带，是多地震发生的国家之一，事实上，海底与陆地一样经常发生地震，虽然地震载荷没有其他环境载荷出现的频率高，且发生时持续时间也较短，但是地震对平台的破坏可能是十分严重的。目前在我国多地震发生的海域修建平台必须进行抗震设计，地震对平台的破坏一般与地震烈度和当地土壤等因素有关[1-2]。另一方面，自升式平台工作时，主要是将桩腿插入海底土中，依靠海底土的支撑力来抵抗外载荷，现有研究[3-6]中，通过各种方法考虑桩土相互作用的非线性影响，或直接将桩基础简化成铰支约束或其他一些简单的约束形式。

本文将综合考虑环境载荷包括地震影响、桩土效应，建立某400英尺自升式钻井平台的三维有限元分析模型，并针对风暴自存状态，对该自升式钻井平台进行动力分析，并与常规分析方法得到的结果进行对比，分析桩土效应、地震等因素对平台动力响应的影响。

1 基本理论

式中：[Ms]、[Cs]和[K]分别为平台结构的质量、阻尼和刚度矩阵。｝和 ｛x｝分别表示平台节点的加速度、速度和位移向量。 ｛F （t ）｝主要为激励力矢量，包括风、浪、流和地震。

其中，结构阻尼矩阵[Cs]采用Rayleigh阻尼形式：

在文中求解运动方程时，采用Newmark时间积分法。

1.1 风载荷

根据CCS《海上移动平台入级与建造》规范[7]第2.2条规定，风压P应按下式计算：

式中：v为设计风速，本文风暴自存状态下取51.44 m/s计算。

作用于构件上的风力F应按下式计算，并应确定合力作用点的垂直高度：

式中：P为风压，kPa；S为平台在正浮或倾斜状态时，受风构件的正投影面积，m2；Ch为受风构件的高度系数，其值可根据构件高度h（构件型心到设计水面的垂直距离）由规范中表2.2.2.1（a）选取；Cs为受风构件形状系数，其值可根据构件形状由规范中表2.2.2.1（b）选取，也可根据风洞试验确定。

1.2 波、流载荷

波、流载荷的计算应选取不同波浪相位角下的结果，以确定波流载荷的危险状态，海流载荷的计算取流向与波浪相位角相同，表面流速取0.77 m/s，按线性规律衰减至海底流速为0。

由于自升式钻井平台的桩腿为桁架式结构，则桩腿上波流载荷可根据Morison公式[8]计算，则单位长度上x向受到的波流力为：

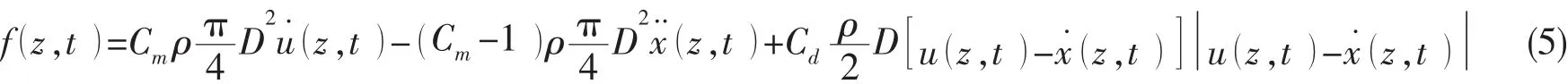
式中：α和β为阻尼系数，由振型阻尼比ξ和自振固有频率ωi有关，其中

1.3 桩土效应

目前在固定式平台的设计中，为简便起见，常将桩基础简化成铰支约束，从而忽略了桩与土之间的非线性效应，文中为便于比较分析，首先将采用传统的简化桩基处理方法，建立桩基础分析模型如图1所示。

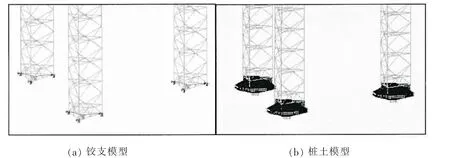
图1 桩基础模型示意图Fig.1 Sketch of the pile foundation model

另一方面，文中也将基于Winkler梁模型理论，假设沿桩基结构连续分布的土反力的强度仅与该点挠度有关，且此处强度不影响该点以外的变形，并在ANSYS软件中建立相应的计算模型，即土按Winkler地基来处理，桩为埋置于土中的梁，桩—土之间的相互作用由一系列频率相关的非线性弹簧来模拟，非线性弹簧的参数可根据分析对象所在海域土质的侧向荷载—位移传递曲线（p-y曲线）、轴向荷载—位移传递曲线（t-z曲线）及桩端荷载—位移传递曲线（q-z曲线）确定，具体分析步骤如下：

（1）建立分析对象的有限元模型，包括分析对象的上部结构，桩腿结构等；

（2）获取分析对象所在海域的土质资料，并根据不同土壤性质对土层进行分层；

（3）计算不同土层对应的p-y曲线、t-z曲线及q-z曲线；

（4）针对每个深度对应的土层建立Combin39单元；

（5）将不同深度下的土壤曲线参数数据作为相应位置Combin39单元的计算参数填入到程序表格中；

（6）对完整分析对象的有限元模型进行相关力学分析。

其中ANSYS软件中Combin39单元[9]是一种具有非线性广义力—变形能力的轴向单元，只需在参数表中输入力—变形的离散点来明确定义Combin39单元的力—变形曲线。

本文中自升式钻井平台桩靴为箱型结构，外观呈正八边形，桩靴入土深度为3.05 m，桩靴边长为5 m，桩靴高度为4.4 m，桩靴底板距桩腿弦杆底部0.62 m，桩靴内部设径向和周向加强板，桩靴的底板、顶板、侧向围板和径向加强板等部位设置加强筋。在建立桩—土动力模型时，应当在桩靴的侧面和底面分别设置相应的弹簧单元，弹簧单元的实常数可以根据该地区相应的土参数求得。

图1给出了两种桩基础模型的示意图，左图为传统的将桩基础简化成铰支约束的铰支模型，右图为基于Winkler地基梁理论的桩土模型。

1.4 地震

地震分析理论一般可分为三类，即静力理论、反应谱理论和直接动力分析理论。静力分析理论是1900年日本大森房吉教授提出的，不考虑结构物的动力特性，认为地震时结构物的运动与地面运动完全一致，结构物的最大加速度等于地面运动的最大加速度，即结构物所受的最大地震载荷F=mamax，该理论由于忽略了结构本身的动力特性的影响，一般只适用于诸如路基、挡土墙等低矮的、刚性较大的建筑。反应谱理论是20世纪40年代美国学者提出的计算地震力的动力方法，它考虑了地震时地面的运动特性与结构自身的动力特性，在当前工程设计中应用得较为广泛，其地震力的最大值可表示为

式中：α=amax/g为水平地震影响系数，我国学者根据国内外数百条地震记录的反应谱进行统计后，建立了地震响应系数与结构自振周期的关系曲线，根据结构所处场地的土的类型不同，可分别从关系曲线中查得相应的影响系数。

由于反应谱理论是以单质点体系在实际地震作用下的反应为基础来分析结构反应，在分析多质点体系时，反应谱仅能给出结构各振型反应的最大值，而丢失了与最大值和振型组合有关的重要信息，且在分析柔度较大的结构时，未能考虑非线性因素的影响，造成较大的计算误差。本文将采用直接动力分析方法即瞬态动力学分析方法，将实际地震的加速度时程记录输入结构计算模型，从而直接获得地震过程中结构节点各时刻的位移、速度和加速度。

2 数值分析

2.1 计算模型

表1给出了自升式钻井平台的主要尺度参数，图2给出了平台的侧视图及相应的有限元分析模型，共有17 584个节点和18 784个单元，其中船体的甲板和舱壁采用SHELL63板壳单元来模拟，骨材和桁材用BEAM188单元模拟，桩腿泥面以上水面以下部分采用PIPE59单元模拟，泥面以下部分采用PIPE20单元模拟。

表2给出了自升式钻井平台自存工况下的环境参数。在实际计算时，选取风、浪、流同向，三者同为0°方向入射。

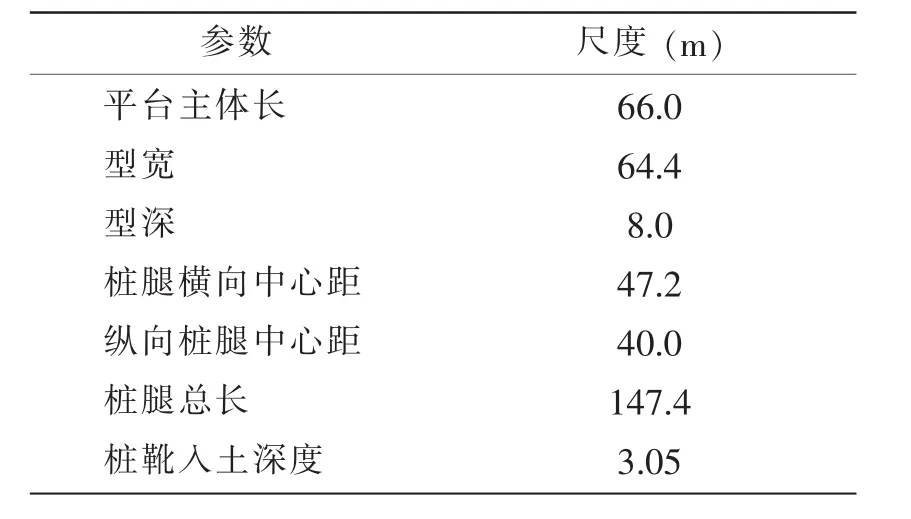
表1 自升式钻井平台主尺度Tab.1 Main dimensions of the jack-up

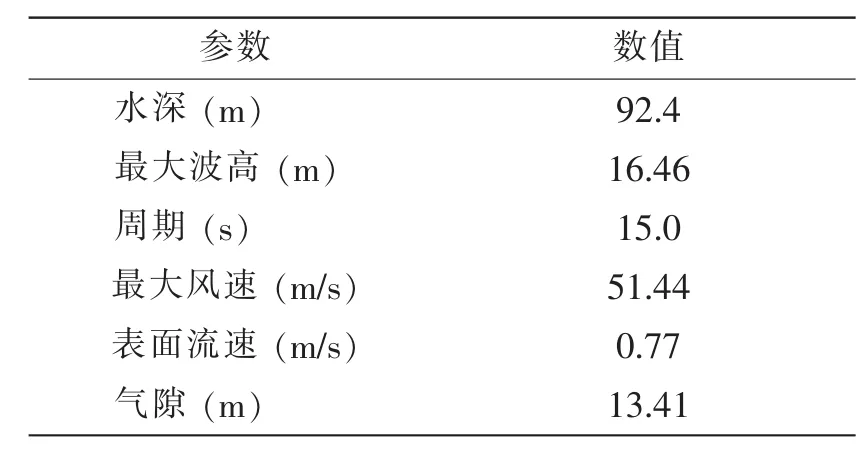
表2 自升式钻井平台风暴自存工况的计算参数Tab.2 Calculation parameters of jack-up under storm survival condition

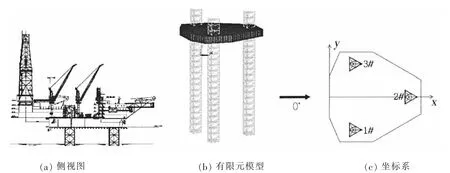
图2 自升式钻井平台Fig.2 The jack-up

2.2 模态分析

模态分析主要是为了确定结构的自振特性（即固有频率和振型），它是承受动态载荷的结构在设计中的重要参数，也是其他动力分析问题的起点。自升式钻井平台承受的环境载荷为动态载荷，同时需知道平台本身的自振周期，与平台所在区的波浪周期对比，以判断出结构发生共振的可能性，因此需对自升式钻井平台进行模态分析。

图3给出了铰支模型和桩土模型的第一阶振型，表3给出了桩基处理方法模态分析得到的平台前六阶自振频率。经过比较，桩土模型的自振频率计算结果均小于铰支模型，分析原因可能是，规范规定的铰支模型，约束条件为桩腿底部铰支，完全约束了x、y和z方向的自由度，但放开了其转动方向的自由度，而本文提出的桩土模型，考虑了土的存在对桩的影响，用一系列参数不同的弹簧单元模拟其相互作用，在桩靴的侧面和底面加了许多弹性支承，与铰支模型相比，约束的整体刚度明显增大，柔度减小，但更接近于地基的实际刚度，因此桩土模型的计算频率要大于规范规定的铰支模型。

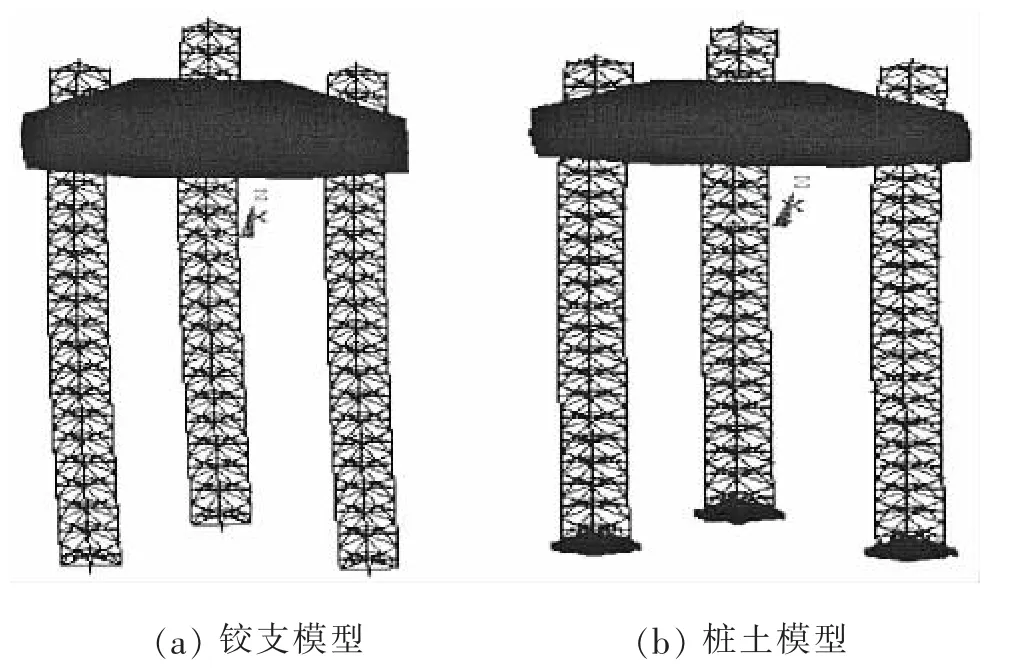
图3 平台第一阶振型Fig.3 First-order vibration mode of platform

表3 平台前六阶自振频率计算结果对比Tab.3 Comparison of first six-order natural vibration of platform

2.3 桩土影响分析

本文自升式钻井平台作业水深较大，相应其自身结构柔度也较大，除承受静荷载以外还受到波浪等动荷载的作用，会引起平台的振动，产生较大位移。为确保安全，仅仅考虑平台的静态效应是不充分的，有必要考虑动力作用，进行平台的动力响应分析。动力响应分析又称时间历程分析，用于计算结构在方位或大小随时间任意变化的载荷作用下的动力学响应，目的是得到结构在受动态作用的情况下位移、应变、应力等随时间变化的解。

本文将分析自升式钻井平台在风暴自存工况下，两种桩基础的动力响应，比较分析平台的最大侧向位移。图4给出两种桩基础下自升式钻井平台桩腿顶端位移时历曲线，表4给出了3根桩腿最大侧向位移的计算结果，为便于比较，同时也列出了相应的静力计算结果。从表中结果可知，与静力分析结果的比较，平台的动力响应比较明显，铰支模型状态下，动力放大系数达到了1.13，而桩土模型状态下动力放大系数也有1.11，这充分说明了自升式钻井平台柔度大的特点，在随时间变化的环境载荷作用下，仅仅对其进行静力分析是不够的。同时，无论静力分析还是动力分析，铰支模型状态下平台桩腿的最大侧向位移始终大于桩土模型状态下的计算结果，且最大增幅达到了31.8%，这主要是因为铰支模型略去了海底基础对桩腿下端的转动约束，此时桩腿底端不能承受弯矩，弯矩全部集中于桩腿与船体的连接处，导致平台桩腿的上部弯矩偏大，从而使得平台桩腿静力和动力分析的侧向位移结果明显偏大。这也充分说明了在自升式钻井平台分析中，传统的桩基础简化模型未能充分考虑海底土对桩基的影响，使得计算结果偏于保守，而本文采用的考虑桩土效应的桩基础模型，充分考虑了平台所在海域海底土对桩基的约束作用，模拟结果更接近真实情况。

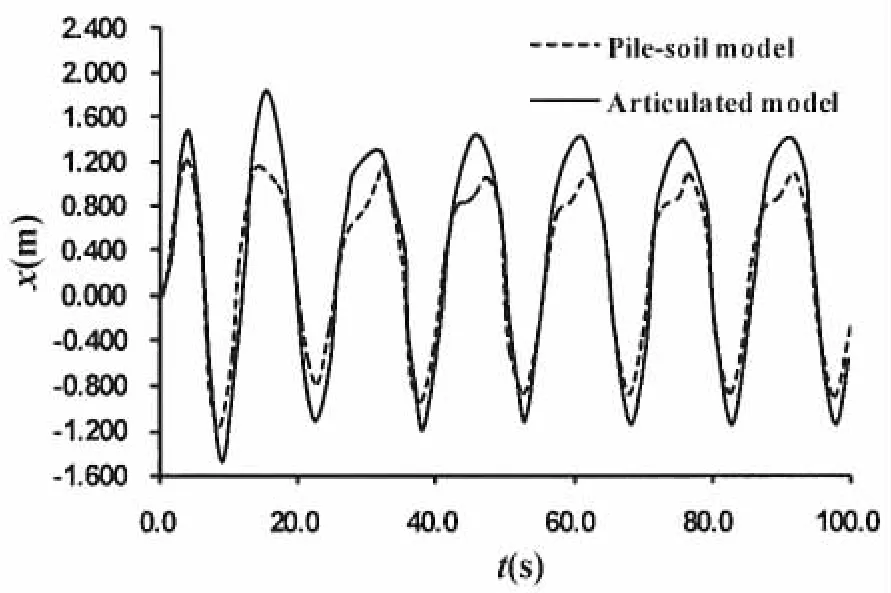
图4 自升式钻井平台最大位移时间历程分析Fig.4 The time history curve of maximum displacement

表4 桩腿最大侧向位移动静力计算结果对比Tab.4 Comparison of maximum lateral displacement of legs

2.4 地震影响分析

地震在海洋中发生频率较高，且一般大地震都发生在海上，并引发海啸等一系列自然灾害。但由于它的不可预见性和偶然性，地震在海洋及海洋工程结构中的记录很少。文中分析中将选用目前常用的宁河天津波，该自升式钻井平台预计设防烈度为7度，平台工作海域属于Ⅲ类场地土，图5给出了宁河天津波水平方向（南北向）和垂直方向的加速度记录，记录时长19.11 s，时间间隔0.01 s，同时考虑到环境载荷作用下，平台的前期时程分析曲线并不稳定，实际地震波加载是从环境载荷作用20 s以后开始。

在计算时，地震水平向输入与环境载荷方向相同即采用水平x方向+竖向地震输入，图6给出了传统铰支模型在环境载荷和地震共同作用下，桩腿顶端x和z向位移时程曲线，图7给出了本文桩土模型在环境载荷和地震共同作用下，桩腿顶端x和z向位移时程曲线。从图中可以看出：（1）传统铰支模型，桩腿顶端z向的位移较小，最大值在0.008 m左右，而桩土模型的桩腿顶端z向位移相对较大，最大值达到了0.17 m，分析原因主要在于铰支模型对桩腿底部z方向的自由度进行了约束，导致竖向的地震波对平台z向运动的贡献非常有限，而桩土模型采用三维的弹簧单元模拟了桩靴和土的接触，可以较真实地反映整个平台在竖向地震波作用下的z向运动；（2）相较于仅考虑环境载荷的作用，叠加了地震波的作用后，平台水平向的位移峰值明显增大，且由于本文采用的地震波为单峰值形式，地震与环境载荷的耦合具有良好的规律性，即两种桩土模型下，平台水平向位移最大值发生时刻仅与两者之间的相位差有关。

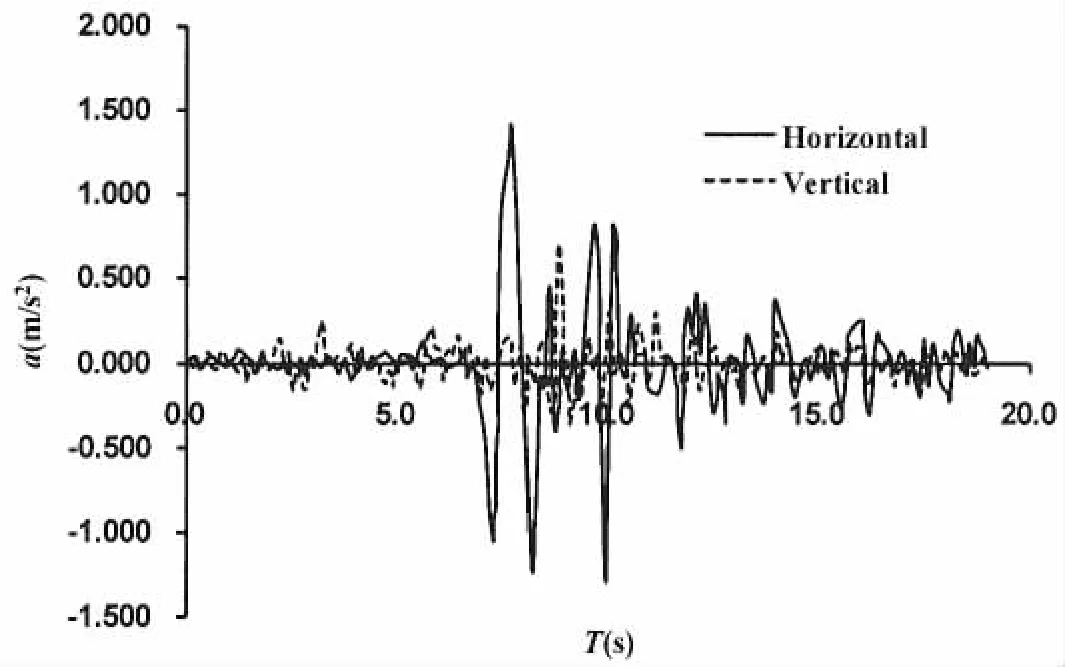
图5 地震波加速度记录Fig.5 The earthquake acceleration record

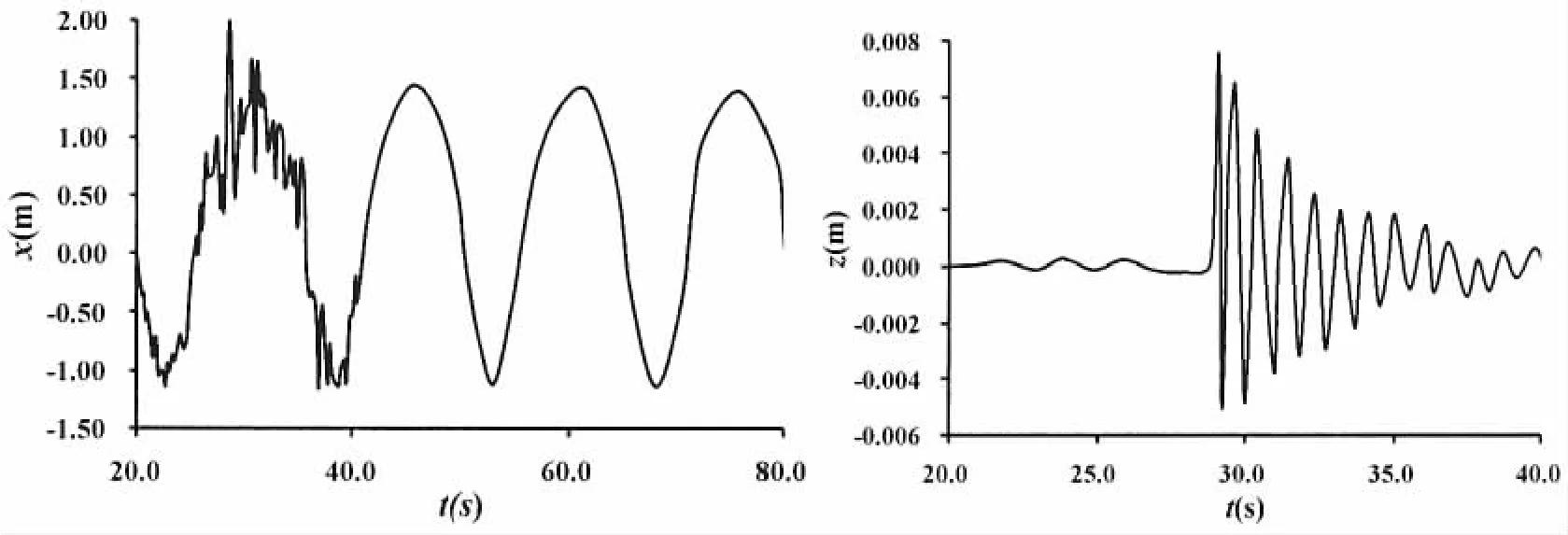
图6 传统铰支模型Fig.6 Traditional articulated foundation model

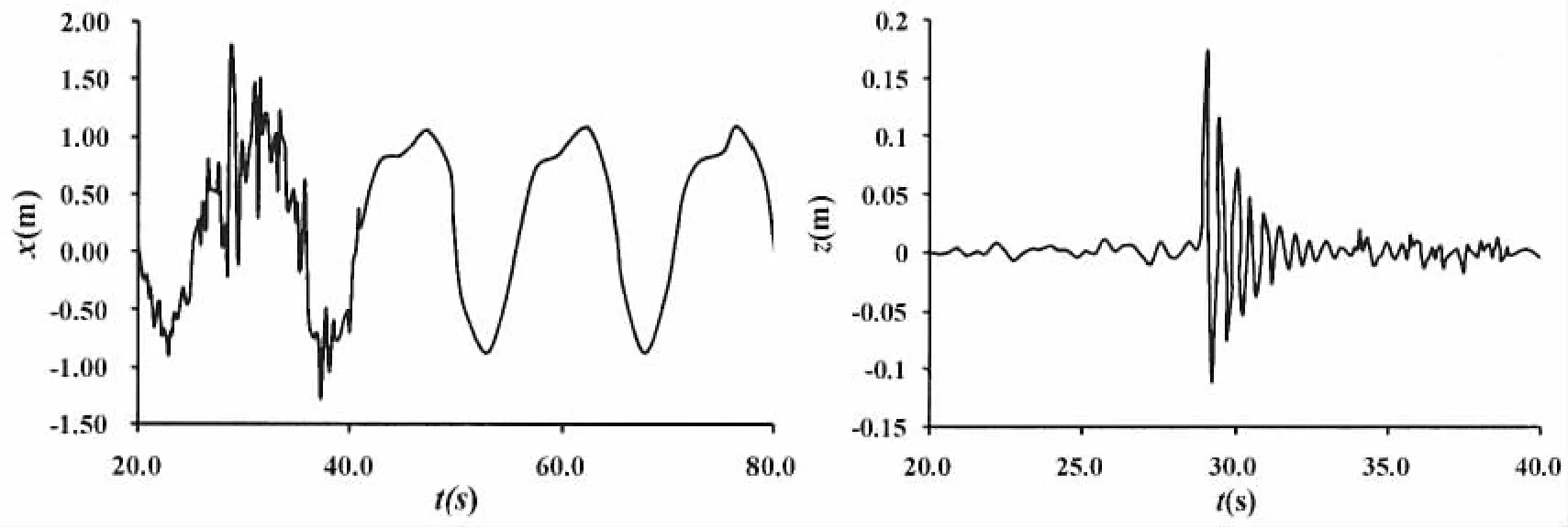
图7 桩土模型Fig.7 Pile-soil foundation model

由于在环境载荷和地震共同作用下，平台水平向最大位移将与两者的相位差有关，上文中计算时实际地震波加载是从环境载荷作用20 s以后开始，从计算得到的时历曲线中可以发现，从20 s开始加载地震波并未得到平台的最大位移值，因此本文编制了相应的地震波加载程序，以1°为间隔循环加载地震波，并搜索相应的环境载荷和地震共同作用下平台的水平向最大位移，最终结果见表5，为便于比较分析，同时列出了未加地震波时，平台仅在环境载荷作用下的最大水平位移值。从表中可以发现：（1）地震波对平台位移的影响较大，两种桩土模型下，叠加地震波后平台的水平向位移值增大幅度在60%以上；（2）地震波对不同桩土模型的影响差别较大，传统的铰支模型加入地震波后，平台水平位移最大值增大了64.2%，而桩土模型增大了91.5%，说明考虑了桩靴和海底土相互作用的桩土模型对地震波更加敏感，这点从平台z向的变化也可得到体现。

表5 平台最大侧向位移结果比较Tab.5 Comparison of maximum lateral displacement of platform

3 结 论

地震与其他环境载荷共同作用下的平台响应分析对研究自升式钻井平台等固定式海洋平台的破坏有重要意义，同时由于自升式钻井平台需要通过桩靴等桩基础与海底土直接接触从而支撑平台抵抗自身和外部荷载，因此在分析平台响应时也必须要考虑桩土效应的影响。本文以某400英尺自升式钻井平台为研究对象，建立了相应的三维有限元分析模型，综合考虑风浪流包括地震等环境载荷和桩土效应的影响，对风暴自存状态下自升式钻井平台的响应进行了分析，研究结果表明：

（1）对两种桩基模型的自升式钻井平台进行了模态分析，结果发现，桩土模型平台的自振频率均小于铰支模型，这主要是由于铰支模型完全约束了平台桩腿底部x、y和z方向的自由度，但放开了其转动方向的自由度，而文中提出的桩土模型，考虑了土的存在对桩的影响，用一系列参数不同的弹簧单元模拟其相互作用，在桩靴的侧面和底面加了许多弹性支承，与铰支模型相比，约束的整体刚度明显增大，柔度减小，但更接近于地基的实际刚度，因此桩土模型的计算频率要大于规范规定的铰支模型；

（2）铰支模型状态下平台桩腿的最大侧向位移大于桩土模型状态下的计算结果，且最大增幅达到了31.8℅，这主要是因为铰支模型略去了海底基础对桩腿下端的转动约束，此时桩腿底端不能承受弯矩，弯矩全部集中于桩腿与船体的连接处，导致平台桩腿的上部弯矩偏大，从而使得平台桩腿静力和动力分析的侧向位移结果明显偏大；

（3）地震对平台动力分析结果的影响较大，两种桩基模型下，叠加地震波后平台的水平向位移值增大幅度在60%以上，且不同的桩基模型考虑地震后增大的幅度也不一样，桩土模型的增大幅度达到了91.5%，说明考虑了桩靴和海底土相互作用的桩土模型对地震波更加敏感，同时地震波与环境载荷之间的相位差对平台动力分析结果也有较大影响。

最后值得特别指出的是，本文主要是探讨桩土效应和地震对自升式平台响应影响的一般规律，所以只是根据参考文献中选择了常用的海底土壤和地震的参数，但实际工程设计时，由于土壤对平台桩基的作用非常复杂，且地震波也不一定是单峰值，因此有必要依据平台实际工作环境的土壤参数和地震记录资料建立更加真实的计算模型来进行分析。

[1]何晓宇,李宏男.地震与波浪联合作用下海洋平台动力特性分析[J].海洋工程,2007,25(3):18-25.He Xiaoyu,Li Hongnan.Dynamic analysis of offshore platform under seismic action and wave action[J].Ocean Engineering,2007,25(3):18-25.

[2]谢礼立,翟长海.最不利设计地震动研究[J].地震学报,2003,25(3):250-261.Xie Lili,Zhai Changhai.Study on the severest real ground motion for seismic design and analysis[J].Acta Seismologica Sinica,2003,25(3):250-261.

[3]Gazetas G,Dobry R.Simple radiation damping model for piles and footings[J].Journal of Engineering Mechanics,1983,110(6):937-956.

[4]刘宗贤,李玉亭.桩基础在阻尼与分层弹性地基场地土波动影响下的横向地震反应分析[J].地震工程与工程振动,1994,14(3):47-59.Liu Zongxian,Li Yuting.The lateral seismic responses analysis for the pile foundation under the influence ofdamping and layer elasto-foundation bed site soil wave motion[J].Earthquake Engineering and Engineering Vibration,1994,14(3):47-59.

[5]Hallan,Moan T,Drange S O.Use of nonlinear pushover analysis in ultimate limit state design and integrity assessment of jacket structures[C].7th International Conference on the Behavior of Offshore Structures,1994:323-345.

[6]李 虎,吴卫国,甘 进.考虑结构桩土相互作用自升式工作平台研究[J].华中科技大学学报,2010,27(3):86-90.Li Hu,Wu Weiguo,Gan jin.Research on multi-purpose offshore jack-up platform based on ANSYS[J].J of HUST(Urban Science Edition),2010,27(3):86-90.

[7]中国船级社.海上移动平台入级与建造规范[S].北京:人民交通出版社,2005.China Classification Society.Standard for classification and construction of offshore mobile platforms[S].Beijing:China Communications Press,2005

[8]竺艳蓉.海洋工程波浪力学[M].天津:天津大学出版社,1991.Zhu Yanrong.Wave mechanics for ocean engineering[M].Tianjin:Tianjin University Press,1991.

[9]杨 进,刘书杰.ANSYS在海洋石油工程中的应用[M].北京:石油工业出版社,2010.Yang Jin,Liu Shujie.The application of ansys in the marine engineering[M].Beijing:Petroleum Industry Press,2010.